深入浅出了解最小二乘法及其应用

  无论是使用线性拟合还是非线性拟合，最小二乘法都是使用它们的基础。关于最小二乘法的数学原理可以给出很多很好的解释，比如可以直接使用多元函数极值的观点，也可以使用线性代数中向量到子空间距离的观点。因为第二种方法比较直观，所以我将用第二种方法来描述最小二乘法这样显得更加直观易懂，而用第一种方法来进行验证。

  1、线性代数方法的描述

   为了表述方便，这里进行一些符号的说明，如下图所示：

图1

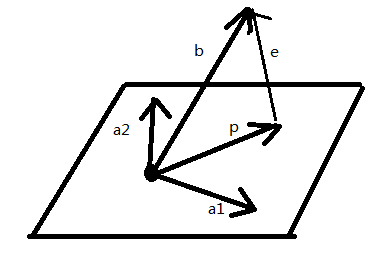
(1) A=[a1, a2]  

(2) p是基向量a1，a2的组合p=x1'a1+x2'a2=Ax'

(3) e=b-p

  2.数学模型(At即为A的转置，x'为x拔)

  图2

  如上图2所示我们解非线性齐次方程Ax=b，显然向量b并不在A的列空间(Col Space)中，即我们无法用A的列向量或是它们的线性组合来表示b，也就是该方程无解。

  虽然我们无法对上面的方程求解x，但是我们可以求其最优解(最近似解)x'，由上图2我们可以看出b在Col Space上的投影p是A的列空间可以表示的最接近的向量。

  下面我们进行下数学描述：

  (1) 令p=Ax'，由图1的正交性可以得出，a1t(b-Ax')=0，a2t(b-Ax')=0

  (2) [a1t ; a2t](b-Ax')=0 即At(b-Ax')=0

  (3) 整理(2)式得AtAx'=Atb  --最小二乘法核心公式

  (4) x'=(AtA) \ Atb --这里为Matlab写法

对(3)进行下简单说明，本来Ax=b是无解的，但是通过对方程两边左乘At，我们可以得到最优解x‘。

  3. 一个实例

图2

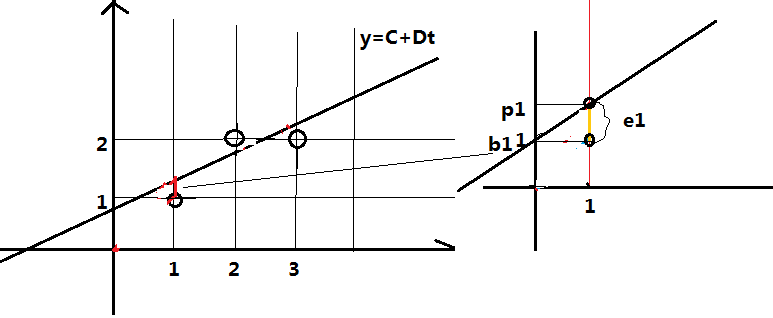
  求Ax=b的最优解

  (1) 绘出一条直接y=C+Dt来拟合图上的三个点(1,1)，(2,2)，(3,2)

  (2) C+D=1，C+2D=2，C+3D=2 =>[1 1 ; 1 2 ; 1 3][C ; D]=[1 ; 2 ; 2]

  (3) 求解最优解x’=[C' ; D'] 

        AtAx'=Atb =>  AtAx'=[1 1 1;1 2 3] [1 1 ; 1 2 ; 1 3][C' ; D']=[3C' 6D' ; 6C' 14D']

                                 Atb=[1 1 1;1 2 3][1;2;2]=[5;11]

        因此3C'+6D'=5

                6C'+14D'=11

         =>C'=2/3  D'=1/2 即所求拟合曲线为y=2/3+1/2t   

 4. 多元函数极值验证

 这里对3进行验证，由图2，既然是最优解

 (1)   使得||Ax-b||^2最小，即||Ax-b||^2=||e||^2=0

 (2) 即使e1^2+e2^2+e3^2=f(C,D)(C+D-1)^2+(C+2D-2)^2+(C+3D-2)^2=0

 (3) 求C,D使得f(C,D)=0，因此对f分别对C,D求偏导等于0，同样得到3C+6D=5，6C+14D=11，证毕。

5. 编写一个Matlab程序来理解最小二乘法的线性与非线性拟合

求数据

x	-3	-2	-1	0	1	2	3
y	4	2	3	0	-1	-2	-5

的最小二乘拟合

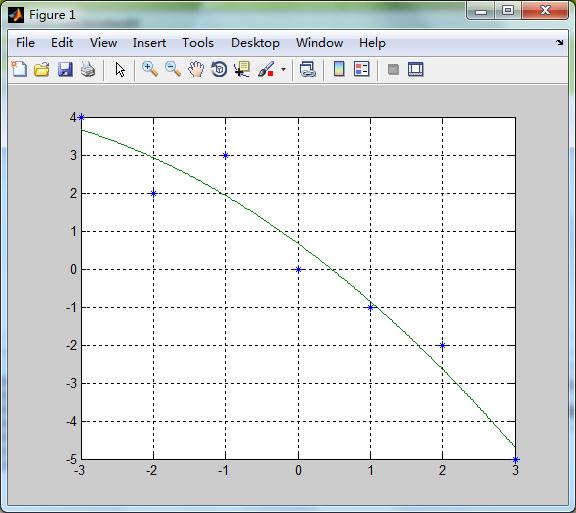
(1) 用y=a0+a1*x+a2*x^2拟合

%最小二乘拟合的主函数
clear
x=[-3 -2 -1 0 1 2 3]';
y=[4 2 3 0 -1 -2 -5]';
% 得到线性方程的系数矩阵
a=[
    zx_nh_f(x(1))
    zx_nh_f(x(2))
    zx_nh_f(x(3))
    zx_nh_f(x(4))
    zx_nh_f(x(5))
    zx_nh_f(x(6))
    zx_nh_f(x(7))
    ];
b=y;
A=a'*a;
B=a'*b;
c=A\B
%得到拟合函数
x_n=-3:0.02:3;
y_n=c(1)*1+c(2)*x_n+c(3)*x_n.^2;
plot(x,y,'*',x_n,y_n)
grid

function f = zx_nh_f( x )  %子函数zx_nh_f
%ZX_NH_F Summary of this function goes here
%   Detailed explanation goes here
f(1)=1;
f(2)=x;
f(3)=x^2;
end

得到结果

c =
    0.6667
   -1.3929
   -0.1310

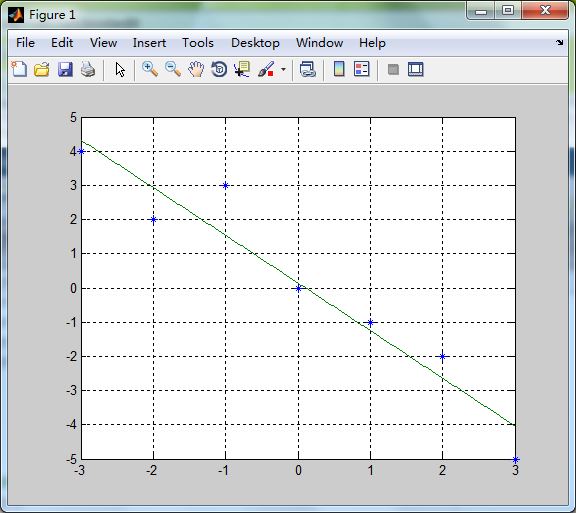
(2) 用y=a0+a1*x拟合

主函数和子函数稍作变化

y_n=c(1)*1+c(2)*x_n; %主函数

%f(3)=x^2;  %删掉

引用：

《MATLAB数值分析与应用_宋叶志》

关于过拟合的概念之前只是草草看过，没深入理解，准备下面有时间再好好看看，所以这里我就先不往下面分析了，研究后再写写。假期后面要做FPGA的项目了，准备把FPGA的项目进展也写写~