阿贝尔-鲁菲尼定理
五次及更高次的多项式方程没有一般的求根公式,即不是所有这样的方程都能由方程的系数经有限次四则运算和开方运算求根。
这个定理以保罗·鲁菲尼和尼尔斯·阿贝尔命名。前者在1799年给出了一个不完整的证明,后者则在1824年给出了完整的证明。埃瓦里斯特·伽罗瓦创造了群论,独立地给出了更广泛地判定多项式方程是否拥有根式解的方法,并给出了定理的证明,但直到他死后的1846年才得以发表。
并不是说明五次或更高次的多项式方程没有解。事实上代数基本定理说明任意非常数的多项式在复数域中都有根.
然而代数基本定理并没有说明根的具体形式。通过数值方法可以计算多项式的根的近似值,但数学家也关心根的精确值,以及它们能否通过简单的方式用多项式的系数来表示。例如,任意给定二次方程
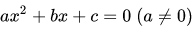
它的两个解可以用方程的系数来表示:
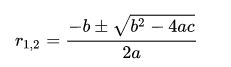
这是一个仅用有理数和方程的系数,通过有限次四则运算和开平方得到的解的表达式,称为其代数解。三次方程、四次方程的根也可以使用类似的方式来表示。阿贝尔-鲁菲尼定理的结论是:任意给定一个五次或以上的多项式方程:

那么不存在一个通用的公式(求根公式),使用 a0,a1,... ,an 和有理数通过有限次四则运算和开根号得到它的解。或者说,当n大于等于5时,存在n次多项式,它的根无法用自己的系数和有理数通过有限次四则运算和开根号得到.
换一个角度说,存在这样的实数或复数,它满足某个五次或更高次的多项式方程,但不能写成任何由方程系数和有理数构成的代数式。这并不是说每一个五次或以上的多项式方程,都无法求得代数解。具体区分哪些多项式方程可以有代数解而哪些不能的方法由伽罗瓦给出,因此相关理论也被称为伽罗瓦理论。简单来说,某多项式方程有代数解,等价于说它对应的域扩张上的伽罗瓦群是一个可解群。对于一般的二次、三次和四次方程,它们对应的伽罗瓦群是二次、三次和四次对称群.
伽罗瓦基本定理的最初应用是在使用伽罗瓦理论证明五次或以上的多项式方程没有代数解求根公式的问题上。其证明的主要思路是将“开n次方”的过程转化为“在基域中添加n次方根”生成的域扩张。将多项式有代数解的问题转化为某个分裂域是否可以通过有限次特定的域扩张得到的问题。而这些域扩张是否满足条件,则可以由伽罗瓦基本定理将其转化为判定“特定的伽罗瓦群是否有某种特殊的子群和商群(称为可解群)”的问题。
代数基本定理:任何一个非零的一元n次复系数多项式,都正好有n个复数根。







 本文解析了阿贝尔-鲁菲尼定理,该定理指出五次及更高次多项式方程没有通用的求根公式,即不能通过简单的代数运算求解。文章还介绍了伽罗瓦理论如何判定多项式方程是否拥有根式解。
本文解析了阿贝尔-鲁菲尼定理,该定理指出五次及更高次多项式方程没有通用的求根公式,即不能通过简单的代数运算求解。文章还介绍了伽罗瓦理论如何判定多项式方程是否拥有根式解。

















 582
582

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










