一随机变量
1、基本概念
随机变量定义:随机变量在不同的条件下由于偶然因素影响,其可能取各种随机变量不同的值,具有不确定性和随机性,但这些取值落在某个范围的概率是一定的,此种变量称为随机变量。
随机变量首先是一个变量。昨天的天气,你的高考成绩都是随机变量,不过这些是确定无疑的,相反随机变量结果不确定。
累计分布函数定义:
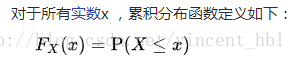
这里X为实随机变量,即取值为实数的随机变量。
2、常见随机变量:
(离散)伯努利变量:变量取值1或0,取值1概率为p,取值0概率为1-p。
期望p,方差p(1-p)。
(离散)二项随机变量:进行n次独立重复实验,每次成功概率p,总共成功次数x是二项随机变量。记为参数为(n,p)的随机变量。二项随机变量可以看做是n个独立同分布伯努利变量的和构成的随机变量。
二项分布分布列(概率质量函数):
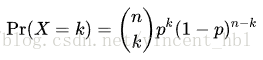
期望np,方差np(1-p)。
(离散)泊松随机变量:现实生活中很多显现服从泊松分布,举几个例子:医院每天接待的病人数、超市某商品每天的销售数、公司每天接到电话数、一本书中错别字个数。这些问题中存在一个单位范围:一天、一页书。这个单位范围中某事件发生的次数就符合泊松分布。参数lambda可以在更大范围统计平均值得到:一年中平均每天病人数、整本书中平均一页错别字数。
一个明显的问题是,为什么这些问题付聪泊松分布,而不是其他的比如正态分布?这个涉及到概率论更高级的问题,叫做泊松过程,如果事件是一个泊松过程,那么它就服从泊松分布。具体学习随机过程教程。
泊松分布 分布列:
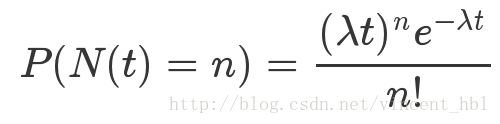
上式表示,在t个单位时间内,发生n次事件的概率。
当t为一个单位时间时,又可以如下表示:
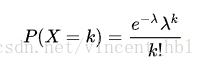
泊松分布的均值、方差都等于参数 λ λ (lambda)
另外,在某些条件下,二项分布可以用泊松分布近似。
(连续)均匀随机变量
概率密度函数:
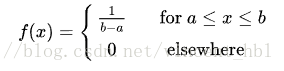
均值方差:
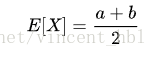
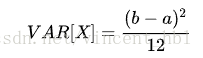
(连续)正态随机变量
正态分布大概是概率论中最重要的随机分布了。一个原因是因为中心极限定理说明了多个随机变量的和服从正态分布。生活中的例子有:身高的分布、测量误差的分布。实际上,正态分布在现实生活中并没有那么常见,相反指数正太分布更常见(即是一个随机变量的对数值服从正态分布)。
正太分布密度函数:
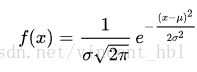
均值方差分别为 μ μ 和 σ2








 本文是《概率论基础教程》的第二部分,详细介绍了随机变量的类型,包括伯努利、二项、泊松等分布,并探讨了期望和方差的概念,以及它们在随机变量中的应用。此外,还提到了随机变量的联合分布、独立性以及协方差,为理解概率论打下坚实基础。
本文是《概率论基础教程》的第二部分,详细介绍了随机变量的类型,包括伯努利、二项、泊松等分布,并探讨了期望和方差的概念,以及它们在随机变量中的应用。此外,还提到了随机变量的联合分布、独立性以及协方差,为理解概率论打下坚实基础。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








