无穷远点、无穷远线与无穷远平面

1、2D平面上的直线

        2D平面上一条直线，可以用 ax1 + bx2 + c = 0 描述，将参数和变量分别提取乘参数，可以用向量 l 和 x 描述。

        以后可以直接说这条直线就是 l , l 决定了这条直线，求直线等同于求 l 。如果一个点属于这条直线，那么直线的方程可以用向量的相乘等于0表示。

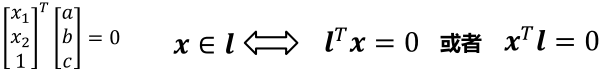
2、2D平面上的直线交点

        两条直线的交点，可以用两个直线的叉乘表示，叉乘的结果为交点坐标。

        证明：

        因此，x 为交点。

3、2D平面上的无穷远点

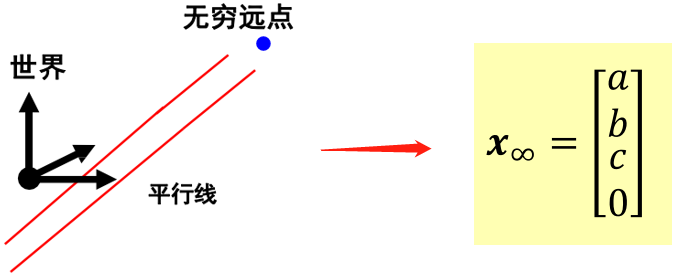
        二维空间中的一个点，可以用3*1维向量表示，齐次坐标中x3 != 0。无穷远点则是齐次坐标最后一维 x3 = 0。（写成欧式坐标，u=x1/x2, v=x2/x3，则x3=0就是无穷远点）

        齐次坐标形式，就可以表达无穷远点，也可以参与计算。这里我们关注两条平行直线交点，结论：平行线的交点在无穷远点，坐标为直线的方向，第三维为0：

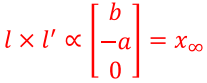
        其中，向量叉乘计算如下：

        证明：

        因此同理可证明该点也位于直线 l` 上。即 [a, b, c] 与 [b, -a, 0]T垂直（T为转置），[a, b] 表示直线的法向量，垂直方向为 [ b, -a]。简单来说一条直线的无穷远点即这条直线的方向，最后一位加 0 就是他们的交点。

4、2D平面上的无穷远直线

        无穷远点集位于称为无穷远线的一条直线上。

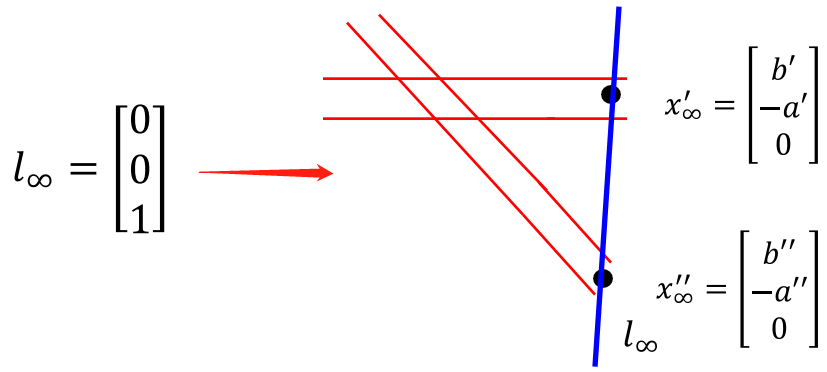
        证明：

        无穷远线可以认为是平面上线的“方向”的集合。PS：两组平行线确定无穷远线。

5、3D空间中的面

        定义3D空间中一平面，齐次坐标表达式如下：

        一个点属于这个平面，也可以表示成如下形式：

6、3D空间中的直线

        3D空间中直线具有4个自由度，难以在空间中表示。可以定义为两平面的交线，只关注直线的方向：

7、3D空间中的无穷远点

        空间中平行线的交点，三维空间中的无穷远点，一定是第四维为0（这里的 a,b,c 就是直线的方向），依据2D空间定义，可定义为：

8、3D空间中的无穷远平面

        1）每一个平面对应着一条无穷远线；

        2）平行平面在无穷远处交于一条公共线，即无穷远直线（即平行平面的无穷远线是同一根）；

        3）两条或多条无穷远直线的集合定义为无穷远平面。