Apollo二次规划的应用之PWJ

  基于之前对二次规划的粗鄙描述： Lattice Planner从学习到放弃（二）：二次规划的应用与调试发现遗漏了如何建立矩阵P…后来再看，其实理解的并不透彻，这次补上。
  Apollo中lattice planner中存在两种求解方法，一种是撒点后根据起始状态直接求解五次多项式，一种是纵向s均匀采样后根据bound构建二次型实现数值优化求解。基于数值优化求解，lattice和pwj在横向规划方面，构建目标函数存在差异，求解过程并无二致。
  引用老哥 决策规划算法四：Piecewise Jerk Path Optimizer 的话：该路径平滑算法用3次多项式连接每个离散点，即每段曲线的Jerk为常数，该算法因此而得名：Piecewise Jerk Path Optimizer.

优化问题解析

  规划的目的是在有限的约束下按照一定目标计算出我们想要的轨迹。即：目标+约束。
  决策：从当前环境中给出一个粗范围，建立一个局部空间将车辆面对的复杂情况凸化，用于后续快速求解
  规划：基于当前空间，求解出符合需求的可行轨迹
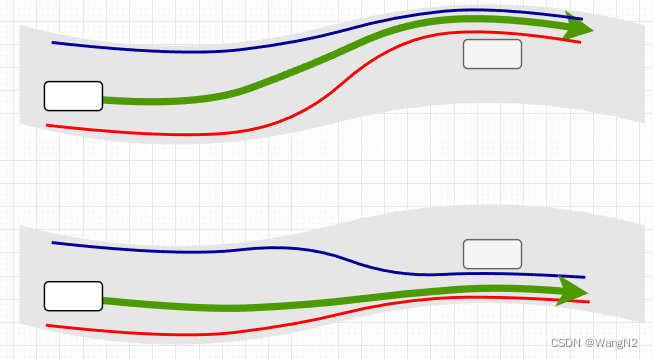
用图说话：

  对于这个场景而言，决策单一且清晰，只需要设置合理的bound，进行规划求解即可。然而，实际的行车条件是复杂多变的，对于下述场景(凹问题，且障碍物还是静止的)，决策结果将会是多样的：左绕行、右绕行、停车。没有合理的决策将会让系统行为显得很傻，一旦明确从左还是从右，剩下的问题自然迎刃而解，这便是决策的重要性。

  Planning优化问题的本质便是在这约束内，计算出最优的轨迹。

二次规划求解

  关键在于如何将规划问题转换成如下QP形式。

构建优化目标

  对于横向规划，以下图情况为例，我们希望自车在车道不沿车道中心线，而是略微靠右行驶：

定义状态量
$$x=[l_0,l_1,...l_n,l_0^{\prime },l_1^{\prime },...l_n^{\prime }，l_0^{\prime \prime },l_1^{\prime \prime },...l_n^{\prime \prime }{]}^T$$
整理优化目标：

• 横向位移
    1.轨迹贴合车道指引线
  $$J_l=\sum _{i=0}^{n-1}{l}_i^2$$
    2.轨迹贴合期望路径
  $$J_{l\_ref}=\sum _{i=0}^{n-1}(l_i-l\_re{f}_i{)}^2$$
    3.指定轨迹目标末点
  $$J_{l_{end}}=\sum _{i=n-1}^{n-1}(l_n-l_{end}{)}^2$$

• 横向速度
    1.轨迹相对于指引线的横向速度
  $$J_{l^{\prime }}=\sum _{i=0}^{n-1}{l}_i^{\prime 2}$$
    2.轨迹相对末点的横向速度
  $$J_{l\_en{d}^{\prime }}=\sum _{i=n-1}^{n-1}(l_i^{\prime }-l\_en{d}^{\prime }{)}^2$$

• 横向加速度
    轨迹相对于指引线的横向加速度
  $$J_{l^{\prime \prime }}=\sum _{i=0}^{n-1}{l}_i^{\prime \prime 2}$$
    2.轨迹相对末点的横向速度
  $$J_{l\_en{d}^{\prime \prime }}=\sum _{i=n-1}^{n-1}(l_i^{\prime \prime }-l\_en{d}^{\prime \prime }{)}^2$$

• 横向加加速度
    轨迹相对于指引线的横向jerk
  $$J_{jerk}=\sum _{i=0}^{n-1}jer{k}_i^2$$
    已知
  $$jer{k}_i=l_i^{\prime \prime \prime }=\frac{l_{i+1}^{\prime \prime }-l_i^{\prime \prime }}{\Delta s}$$
    可得横向jerk最终形式为
  $$J_{jerk}=\sum _{i=0}^{n-1}(\frac{l_{i+1}^{\prime \prime }-l_i^{\prime \prime }}{\Delta s}{)}^2$$
  最终，我们对每种优化目标施以权重来得到最终的优化目标：
  $$\begin{gathered} J_{target}=W_l\cdot J_l+W_{l_{ref}}\cdot J_{l\_ref}+W_{l_{end}}\cdot J_{l_{end}}+W_{l^{\prime }}\cdot J_{l^{\prime }}+W_{l\_en{d}^{\prime }}\cdot J_{l\_en{d}^{\prime }}+W_{l^{\prime \prime }}\cdot J_{l^{\prime \prime }}+W_{l\_en{d}^{\prime \prime }}\cdot J_{l\_en{d}^{\prime \prime }}+W_{jerk}\cdot J_{jerk} \\ =(W_l+W_{l_{ref}})\cdot \sum _{i=0}^{n-1}{l}_i^2-2W_{l_{ref}}\cdot \sum _{i=0}^{n-1}{l}_i\cdot l\_re{f}_i+W_{l_{ref}}\cdot \sum _{i=0}^{n-1}{l}_{ref}^2+W_{l_{end}}(l_{n-1}{)}^2-2W_{l_{end}}\cdot l_{n-1}{l}_{end}+W_{l_{end}}(l_{end}{)}^2 \\ +W_{l^{\prime }}\cdot \sum _{i=0}^{n-1}{l}_i^{\prime 2}+W_{l_{end}^{\prime }}(l_{n-1}^{\prime }{)}^2-2W_{l_{end}^{\prime }}\cdot l_{n-1}^{\prime }{l}_{end}^{\prime }+W_{l_{end}^{\prime }}(l_{end}^{\prime }{)}^2 \\ +W_{l^{\prime \prime }}\cdot \sum _{i=0}^{n-1}{l}_i^{\prime \prime 2}+W_{l_{end}^{\prime \prime }}(l_{n-1}^{\prime \prime }{)}^2-2W_{l_{end}^{\prime \prime }}\cdot l_{n-1}^{\prime \prime }{l}_{end}^{\prime \prime }+W_{l_{end}^{\prime \prime }}(l_{end}^{\prime \prime }{)}^2 \\ +W_{l^{\prime \prime \prime }}\cdot (\frac{1}{\Delta s}{)}^2\cdot \sum _{i=0}^{n-1}(l_{i+1}^{\prime \prime 2}+l_i^{\prime \prime 2})-2W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}\cdot \sum _{i=0}^{n-1}{l}_{i+1}^{\prime \prime }{l}_i^{\prime \prime } \\ =(W_l+W_{l_{ref}})\cdot \sum _{i=0}^{n-1}{l}_i^2+W_{l_{end}}(l_{n-1}{)}^2+W_{l^{\prime }}\cdot \sum _{i=0}^{n-1}{l}_i^{\prime 2}+W_{l_{end}^{\prime }}(l_{n-1}^{\prime }{)}^2+(W_{l^{\prime \prime }}+W_{l^{\prime \prime }}\cdot \frac{1}{\Delta s^2})\cdot \sum _{i=0}^{n-1}{l}_i^{\prime \prime 2}+W_{l^{\prime \prime }}\cdot \frac{1}{\Delta s^2}\cdot l_{i+1}^{\prime \prime 2}-2W_{l_{ref}}\cdot \sum _{i=0}^{n-1}{l}_i\cdot l\_re{f}_i-2W_{l_{end}}\cdot l_{n-1}{l}_{end}-2W_{l_{end}^{\prime }}\cdot l_{n-1}^{\prime }{l}_{end}^{\prime }-2W_{l_{end}^{\prime \prime }}\cdot l_{n-1}^{\prime \prime }{l}_{end}^{\prime \prime }+Const \end{gathered}$$

拆解目标函数为二次型形式

  目标函数已经列完，合并该合并的，常数项统统并为const，并不会影响目标求解。根据状态量x，
矩阵P如下：
$$\left[\begin{array}{cccccccccccccc}{W}_l+W_{l_{ref}}& 0& \cdots & \cdots & 0& 0& \cdots & \cdots & 0& 0& \cdots & \cdots & \cdots & 0\\ 0& W_l+W_{l_{ref}}& 0& \cdots & ⋮& ⋮& \cdots & \cdots & ⋮& ⋮& \cdots & \cdots & \cdots & ⋮\\ ⋮& 0& W_l+W_{l_{ref}}& 0& ⋮& ⋮& \cdots & \cdots & ⋮& ⋮& \cdots & \cdots & \cdots & ⋮\\ ⋮& ⋮& 0& \ddots & 0& ⋮& \cdots & \cdots & ⋮& ⋮& \cdots & \cdots & \cdots & ⋮\\ 0& \cdots & \cdots & 0& W_l+W_{l_{ref}}+W_{l_{end}}& 0& \cdots & \cdots & ⋮& ⋮& \cdots & \cdots & \cdots & ⋮\\ 0& \cdots & \cdots & \cdots & 0& W_{l^{\prime }}& 0& \cdots & ⋮& ⋮& \cdots & \cdots & \cdots & ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& 0& W_{l^{\prime }}& 0& ⋮& ⋮& \cdots & \cdots & \cdots & ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& 0& \ddots & 0& ⋮& \cdots & \cdots & \cdots & ⋮\\ 0& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & 0& W_{l^{\prime }}+W_{l_{end}^{\prime }}& 0& \cdots & \cdots & \cdots & ⋮\\ 0& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & 0& W_{l^{\prime \prime }}+W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}& 0& \cdots & \cdots & ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& 0& -2W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}& W_{l^{\prime \prime }}+2W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}& 0& \cdots & ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& 0& \ddots & \ddots & 0& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& 0& -2W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}& W_{l^{\prime \prime }}+2W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}& 0\\ 0& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & -2W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}& W_{l^{\prime \prime }}+W_{l^{\prime \prime \prime }}\cdot \frac{1}{\Delta s^2}\end{array}\right]$$
矩阵Q如下：
$$\left[\begin{array}{c}-2\cdot W_l\cdot l_{ref}\\ ⋮\\ ⋮\\ -2\cdot W_l\cdot l_{ref}\\ -2\cdot W_l\cdot l_{ref}-2\cdot W_{l_{end}}\cdot l_{ref}\\ 0\\ ⋮\\ 0\\ -2\cdot W_{l_{end}^{\prime }}\cdot l_{ref}^{\prime }\\ 0\\ ⋮\\ 0\\ -2\cdot W_{l_{end}^{\prime \prime }}\cdot l_{ref}^{\prime \prime }\end{array}\right]$$
高能预警：上述优化目标函数中，ds为定值即求解过程为定步长，在实际问题建立中，s一旦不为定步长，将会导致求解结果不符合预期。

构建约束

  PWJ约束定义没有本质区别，依然是满足运动学约束，外加横向jerk bound，可戳：Lattice Planner从学习到放弃（二）：二次规划的应用与调试

代码实现

Apollo源码里结构很清晰，主体函数：

bool PiecewiseJerkProblem::Optimize(const int max_iter) {
  OSQPData* data = FormulateProblem();
  ...
}

在FormulateProblem()函数中实现二次型的构建：

OSQPData* PiecewiseJerkProblem::FormulateProblem() {
  // calculate kernel
  std::vector<c_float> P_data;
  std::vector<c_int> P_indices;
  std::vector<c_int> P_indptr;
  CalculateKernel(&P_data, &P_indices, &P_indptr);

  // calculate affine constraints
  std::vector<c_float> A_data;
  std::vector<c_int> A_indices;
  std::vector<c_int> A_indptr;
  std::vector<c_float> lower_bounds;
  std::vector<c_float> upper_bounds;
  CalculateAffineConstraint(&A_data, &A_indices, &A_indptr, &lower_bounds,
                            &upper_bounds);

  // calculate offset
  std::vector<c_float> q;
  CalculateOffset(&q);

  OSQPData* data = reinterpret_cast<OSQPData*>(c_malloc(sizeof(OSQPData)));
  CHECK_EQ(lower_bounds.size(), upper_bounds.size());

  size_t kernel_dim = 3 * num_of_knots_;
  size_t num_affine_constraint = lower_bounds.size();

  data->n = kernel_dim;
  data->m = num_affine_constraint;
  data->P = csc_matrix(kernel_dim, kernel_dim, P_data.size(), CopyData(P_data),
                       CopyData(P_indices), CopyData(P_indptr));
  data->q = CopyData(q);
  data->A =
      csc_matrix(num_affine_constraint, kernel_dim, A_data.size(),
                 CopyData(A_data), CopyData(A_indices), CopyData(A_indptr));
  data->l = CopyData(lower_bounds);
  data->u = CopyData(upper_bounds);
  return data;
}

---

拓展

  对于纵向规划而言，换汤不换药，只不过状态量变成了s和t相关。
  对于pwj中函数：

piecewise_jerk_problem.set_x_ref()

可好好利用，通过设置x_ref可以通过软约束的行驶达到使车辆基于参考线实现偏移目的。
  对于osqp求解器的实际求解过程，em…大神的文章着实给力：
路径规划中不得不知的OSQP
交替方向乘子法（ADMM）算法的流程和原理是怎样的

思考

  得力于现在的工作环境，最近一直在从事基于规则优化的规划和基于ML的DDP(Data Driven Planning)规划，目前行业对数据驱动以及深度学习用于规划也是热火朝天，毕竟随着数据的指数级增长，如何使用这些海量数据成了Tire1和车企绕不开的问题。大量数据训练用以驱动自动驾驶的趋势显而易见。对于二者的配合方式，自己也有了一些困惑：ML为主，rule base只用于最后的兜底？亦或是 rule base为主，ML为其提供决策指导？ 毕竟开车不是下棋，一步错棋或许还能补救，一个异常轨迹可能就是一个家庭。
  虽然我司采用第一种且效果还不错，但面对依然偶发的异常行为，如果目的是快速落地并真正的服务于大众，或许第二种是最直接和稳定的？期待大佬给锤~~

---

每天进步一点点…come on