二维傅里叶旋转定理证明_旋转磁场理论（Drehfeldtheorie）（一）

本文主要介绍以下几个概念：

• 什么是旋转磁场
• 傅里叶分析下的电流空间分部、气隙分布以及磁感应强度分布

(Strombelagswellen, Leitwertwellen, Induktionsdrehwellen)

1. 旋转磁场

什么是旋转磁场，先举个条形磁铁的例子

图 1-1

磁铁或者通电线圈有附近存在磁场，磁感线的疏密表示磁场大小，方向表示磁场方向。为了简化表示，取其主磁通方向（磁铁内从是指向N表示）。将这个条形磁铁旋转可以得到一个圆形旋转磁场。

旋转磁场：磁感应矢量在空间以固定频率旋转的一种磁场。

图 1-2

上图右边每一个箭头表示不同时间下磁铁主磁通的位置。

旋转一个通电线圈也能得到相同的效果。但是如果这线圈通的不是直流电，而是交流电呢？

图 1-3

首先假设线圈不动，那么不同时刻它的幅值不一样，如上图左侧。这时叫做变化场（Wechselfeld）。图1-2中右侧由条形磁铁旋转得到磁场我们叫做圆场。圆场和变化场叠加可以得到椭圆场，椭圆场和圆场都是旋转场。

它们的数学描述如下：

b表示瞬时磁场大小，B表示磁场的幅值，p为极对数可以简单假设为1，x是圆周上的位置，ωt是角速度*时间。

假设有两个磁铁。磁铁2放置于桌面，磁铁1悬挂于其上方，让悬挂的磁铁1旋转，磁铁2会跟着同步旋转。磁铁1的作用即创造一个旋转磁场。如果我们能用线圈生成一个旋转磁场，那么磁铁2就是转子，这是永磁同步电机，如果磁铁2也使用电流励磁的线圈那这就是普遍意义的同步电机。

那么如何利用不动的线圈产生旋转磁场？

2. 电流分布，气隙以及磁感应的傅里叶分析

计算由线圈产生的磁场需要用到安培环路定理

能够影响H的有电流，积分路径。而B=H。由于：

• 由于铁芯部分μ很大
• 磁通不变原则（在整个磁路上B近似不变）

铁芯内的H很小，可以忽略。由安培环路定理可以得到

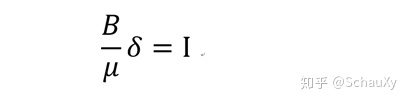
这里δ表示气隙长度。

所以为了计算磁感应强度，我们需要知道电流I和气隙长度δ。

接下来我们将探索同步电机分析其是否产生了旋转磁场。

2.1 电流分布的傅里叶分析（Strombelagswellen）

首先是分析电流，在同步电机里，电流不再仅仅在一根导线内流过，而是许多绕组。我们希望得到电流在周向上的分布，简称电流分布。(Strombelagswellen)

图 2-1-1

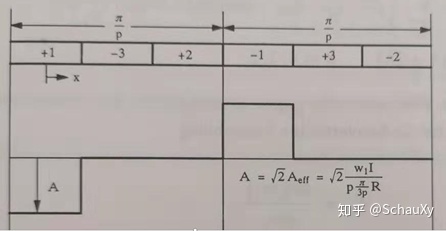
图2-1-1展示了同步电机定子的绕组分布，1、2、3分布代表了3相，正负号是由于线圈在轴向（垂直于纸面）的进出不同。电流分布写作a，A表示最大值。

以第一相为例,由于同相线圈电流一致，所以对应的电流分布相等。

来源于有效值，w1是线圈数量，p可以依旧等于1，分母就是周向的弧长。那么电流分布可以写成一个分段函数

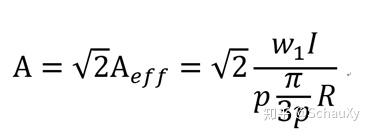
这里引入t变量，考虑到交流电的变化。对这个分段函数进行傅里叶分解可以得到

其中v表示频次，cos(vx)和

都是由傅里叶分解得到的量，sin则是描述电流本身的变化。旋转电机（这里指同步和异步，因其都是旋转磁场，所以叫旋转电机）一共有三相。每相之间空间位置有变化，电流也有120度的相移。所以三相叠加可得

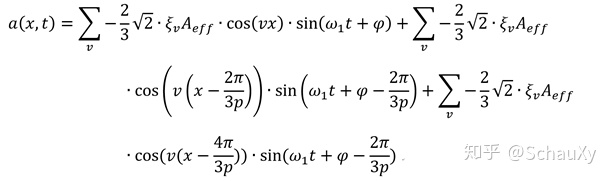
之后则是三角函数的一顿蛇皮操作，得到

此时一看，对比之前圆场的数学描述，发现电流分布在数学形式上是由无数个圆场的叠加而来的。

“那岂不是？”

“啪！并没有。”

注意，一直到现在为止讨论的都是电流分布a( x, t)，它与磁感应b( x, t)之间还有一个积分过程，并且需要气隙δ联系。其次不同频率的圆场叠加后并不是圆场！甚至不是椭圆场，圆场和椭圆场的的幅值在相同空间位置是固定的，而不同频率叠加场同一位置的幅值也不一样。但是，请注意这之中有个计算因子

，如果

接近1，其它很小可以忽略的话那就是一个圆场了。事实情况中，

一般接近1，其它因子很小。

总结一下，我们希望用通电线圈建立旋转磁场，以3相电机为例，使用了傅里叶分析得到其电流分布近似于圆场磁场，但是同时存在高次谐波（）。。那么是否只有3相电机能达到这个效果呢？答案是否定的，通过调节相数、线圈的分布（空间因素），和每相电流的相移（时间因素）可以达到类似的效果。

到这里我们需要思考一个问题，旋转磁场有什么意义？

假设在上述磁场中有一个同步旋转的磁铁，如果是圆形场，那么它受到的力矩在各个位置都是相等的；如果是椭圆场则在不同的位置有不同的力矩；如果有多个大计算因子

的谐波，则会随着时间出现力矩的波动。

我们把由于空间位置带来的力矩变化叫做振动（Schwankungen），由时间带来的变化叫做谐波（Wellen）。

之前的论述过程中，傅里叶分解采取了黑箱处理。一个周期函数可以分解成无数个三角函数的叠加，影响分解后函数表达式的因素是分解前的“函数形状”。下图给出几个常见周期函数的傅里叶分解。

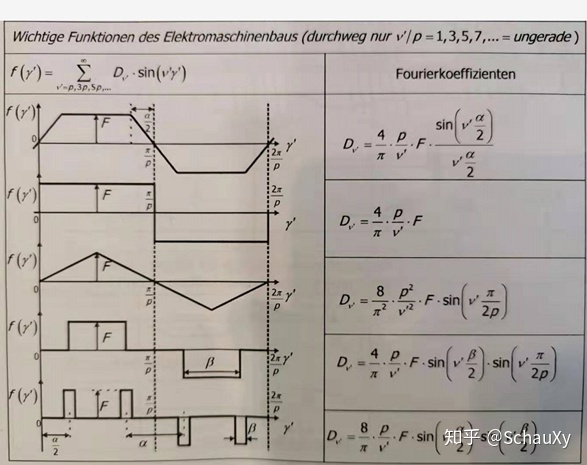
2.2 磁导值（Leitwert）和磁感应强度

磁感应强度除了受到电流还受到气隙宽度δ以及μ的影响，这里我们定义一个新的量——磁导值Λ，它将这两个涵盖了进去。

δ指气隙宽度，δ在轴向分布上一般不是恒值（由于线圈开槽等原因）。但是也可以用傅里叶分解得到一系列的三角函数合。δ"是虚拟气隙宽度。上标的两撇，第一撇表示旋转时转子的偏心，第二撇表示考量了磁饱和现象，磁饱和现象带来的波动也归纳入δ之中，这也是δ( x, t)中有时间变量的原因。

图 2-2-1

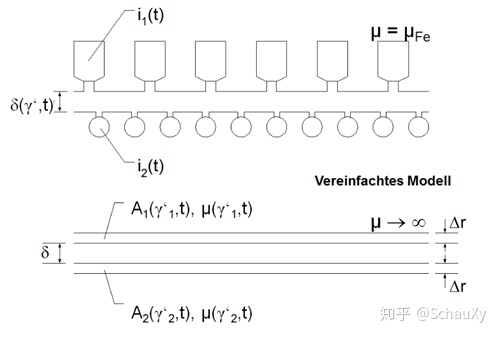
有了电流分布，磁导值根据安培环路定理（忽略铁芯部分）可以给出磁感应强度的计算公式了

式中v( x, t) 表示磁动势，即安培环路公式的左侧电流之合。积分常数项c(t)是由于绕组头有电流流过在定子和转子之间产生了磁通量。

图 2-2-2

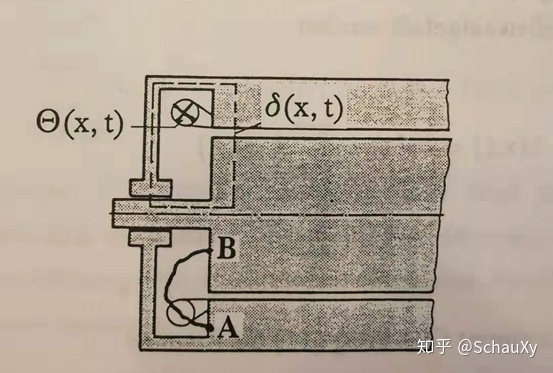
如上图我们之前讨论的所有电流都是取一个圆形横截面，电流流向是轴向的。但是在两端绕组头处还有周向流动的电流。

为了便于理解，先假设磁导值磁Λ为常数，同时c(t)=0。事实上绕组端头的设计会使得c(t)=0磁感应强度与电流的关系为

其中

图 2-2-3

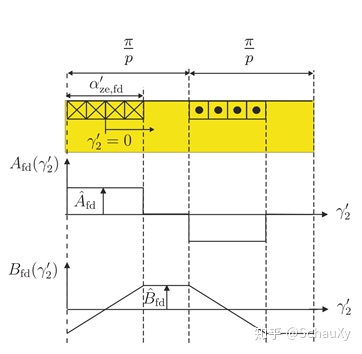
电流分布和磁感应的积分关系如图2-2-3所示

如果Λ为不为常数，

这个公式就是将磁导值

( x, t)的傅里叶分解形式与电流分布a( x ,t) 带入了安培环路定理得到。λ是磁导值

的频次，v是电流分布a( x, t)的分布。c(t)的公式暂且略过，因为我不会。

总结一下，到这里我们完成了：

1.三相交流电励磁定子的磁感应强度b( x, t)的数学描述

2.明白了电流分布a(x,t)和

对b(x,t)的影响

3. 给出了两个重要定义振动（Schwankungen）和谐波（Wellen）

4.安培环路定律在旋转磁场的表达式

5.得到了

，c(t)=0条件下的b(x,t)

6.也得到了b(x,t)的完全描述