| 第6章 | 回到目录 | 第8章 |
|---|
第7章-二阶时滞多智能体系统分组一致性
7.1 引言
分组一致性主要考虑两个关键因素:
- 分组一致性的具体收敛状态
- 分组收敛的速度
一般采用牛顿第二定律进行描述
牛顿第二定律又称为“加速度定律”。
牛顿第二定律被誉为经典力学的灵魂。在经典力学里,它能够主导千变万化的物体运动与精彩有序的物理现象。牛顿第二定律的用途极为广泛,它可以用来设计平稳地耸立于云端的台北101摩天大厦,也可以用来计算从地球发射火箭登陆月球的运动轨道。
牛顿第二定律是一个涉及到物体运动的理论,根据这定律,任意物体的运动所出现的改变,都是源自于外力的施加于这物体。这理论导致了经典力学的诞生,是科学史的一个里程碑,先前只是描述自然现象的理论不再被采纳,取而代之的是这个创立了一种理性的因果关系架构的新理论。
牛顿第二定律
相比于一阶时滞网络,二阶系统一致性需要考虑两个物理量,即速度和位置。
牵制控制的基本思想是: 通过有选择地对网络中的少部分节点施加控制而使得整个网络具有期望的行为。比起对所有节点进行控制的方式,由于较小的资源花费,对网络的小部分节点应用局部反馈控制的牵制控制是更有吸引力和令人期待的。
当考虑系统动态环节后, 系统将可能遇到 Hopf 分岔 (Hopf bifurcation, HB) 现象, 相应的失稳为振荡型失稳。
微分方程理论在自动控制、航天技术、生态生物等方面一直有着广泛的应用,在这些实际应用中,系统通常都是一些含有参数的微分方程组。考虑如下形式的系统:
d X / d t = f ( X , λ , μ ) (1) dX/dt=f(X, λ,μ) \tag{1} dX/dt=f(X,λ,μ)(1)
系统(1)的解显然随参数μ的变化而变化。如果 λ λ λ 在 λ λ λ 等于一个确定值的一个小邻域内变化时,系统(1)在相空间的相图拓扑结构发生了变化,那么就称系统发生了分岔,称 λ λ λ 为分岔参数, λ λ λ 的确定值为分岔值。
而今在应用数学中,Hopf 分岔理论已经成为研究微分方程小振幅周期解产生和消亡的经典工具。因此,对 Hopf 分岔的研究是十分有意义的。
7.2 预备知识
包含
n
+
m
n+m
n+m 个智能体的二阶连续系统如下:
x
˙
i
(
t
)
=
v
i
(
t
)
v
˙
(
t
)
=
u
i
(
t
)
,
i
=
1
,
2
,
⋯
,
m
+
n
(7.1)
\dot{x}_i(t) = v_i(t)\\ \dot{v}(t) = u_i(t),\quad i=1,2,\cdots,m+n \tag{7.1}
x˙i(t)=vi(t)v˙(t)=ui(t),i=1,2,⋯,m+n(7.1)
7.3 问题描述与分析
不同时滞影响下二阶系统的一致性协议:
u
i
(
t
)
=
α
∑
v
j
∈
N
i
a
i
j
(
x
j
(
t
−
T
i
j
)
−
x
i
(
t
−
T
)
)
+
β
∑
v
j
∈
N
i
a
i
j
(
v
j
(
t
−
T
i
j
)
−
v
i
(
t
−
T
)
)
,
i
=
1
,
2
,
⋯
,
N
(7.2)
\begin{aligned} u_i(t) = &\red{\alpha}\sum_{v_j\in N_i} a_{ij} (\red{x}_j(t-T_{ij}) - \red{x}_i(t-T)) + \\ &\red{\beta}\sum_{v_j\in N_i} a_{ij} (\red{v}_j(t-T_{ij}) - \red{v}_i(t-T)),\quad i=1,2,\cdots,N \tag{7.2} \end{aligned}
ui(t)=αvj∈Ni∑aij(xj(t−Tij)−xi(t−T))+βvj∈Ni∑aij(vj(t−Tij)−vi(t−T)),i=1,2,⋯,N(7.2)
α , β \alpha,\beta α,β 分别为该系统的耦合强度。
耦合强度
定理7.1
考虑包含 n + m ( n , m > 1 ) n+m(n,m>1) n+m(n,m>1) 个智能体的多智能体系统(7.4),基于入度平衡的假设条件(A1)和(A2),当网络拓扑结构中包含全局可达节点时,若满足 d ~ i ( α cos ( ω i 0 T i ) + β ω i 0 sin ( ω i 0 T i ) ) < 1 2 ω i 0 2 \tilde{d}_i(\alpha \cos(\omega_{i0} T_i) + \beta \omega_{i0} \sin(\omega_{i0} T_i)) < \frac{1}{2} \omega_{i0}^2 d~i(αcos(ωi0Ti)+βωi0sin(ωi0Ti))<21ωi02 成立,则称系统能渐进实现分组一致。其中 d ~ i = ∑ k = 1 , k ≠ i m + n a i k \tilde{d}_i = \sum_{k=1,k\ne i}^{m+n} a_{ik} d~i=∑k=1,k=im+naik, ω i 0 \omega_{i0} ωi0 表示圆盘中心 G i 0 ( j ω ) = d ~ i e − j ω T i j ω α + β j ω j ω G_{i0}(j\omega)=\tilde{d}_i \frac{e^{-j\omega T_i}}{j\omega} \frac{\alpha+\beta j \omega}{j\omega} Gi0(jω)=d~ijωe−jωTijωα+βjω 的奈奎斯特曲线与复平面实轴的交点,同时 tan ( ω i 0 T i ) = β α ω i 0 \tan(\omega_{i0} T_i) = \frac{\beta}{\alpha} \omega_{i0} tan(ωi0Ti)=αβωi0。
7.4 例子与数值仿真


以上工作,几经尝试,未出现一次收敛的情况。
第二天,换一种新思路来进行


当未进行任何更改时(即权重全都保持1,未添加任何时滞,并且为删除掉不同组的节点状态),直接出现了收敛状态。
结果如下图所示
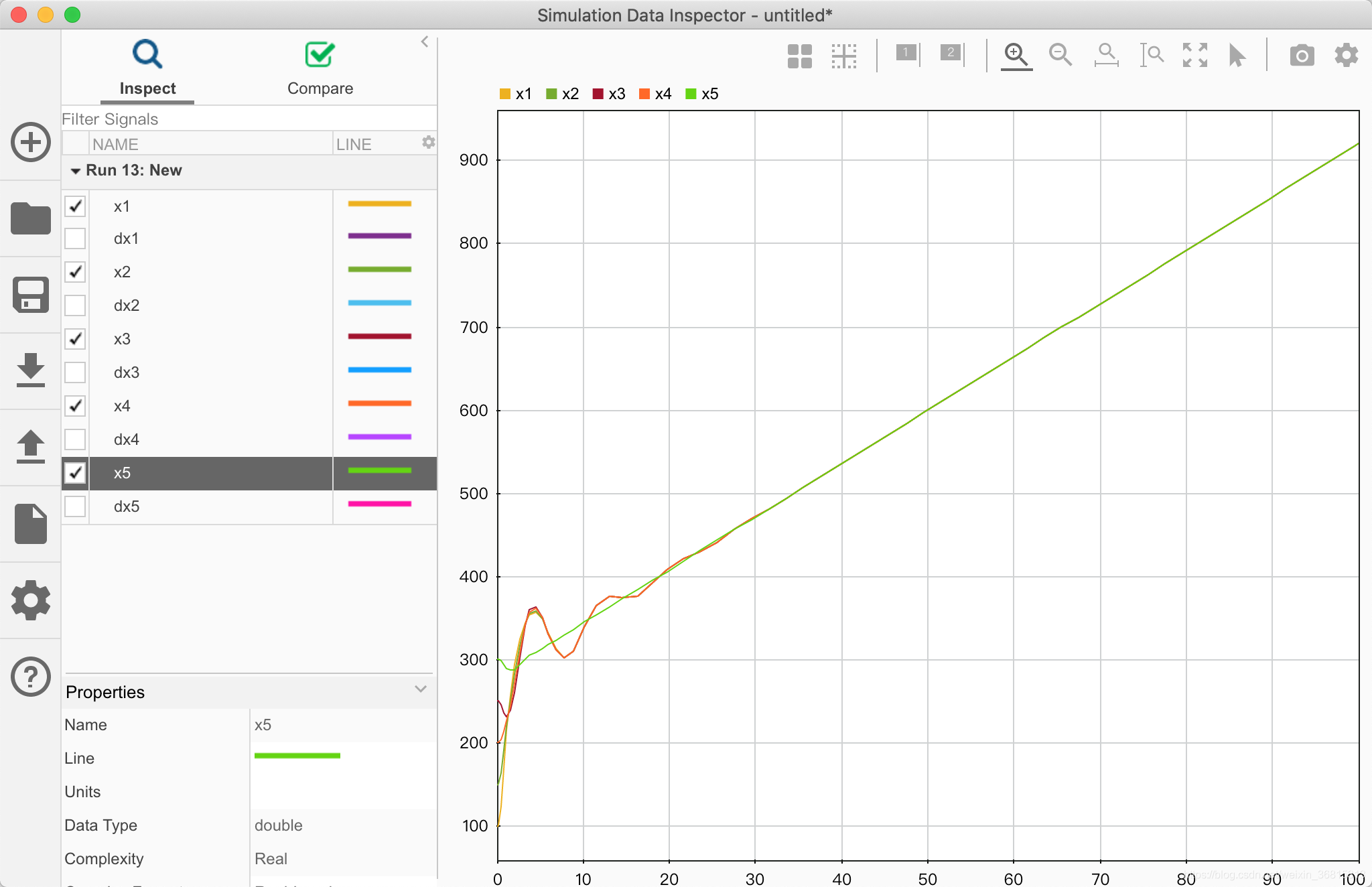

在此基础上更改权重后,
状态信息如下:

速度信息如下:

更改权重之后,再将不同组节点的状态值删除掉


更改 aij 为入度
对比之前的发现一个有趣的现象,虽然状态同样还是发散,但是分组情况发生了变化。
之前使用出度时,1 4 5 为一组,2 3 为一组;
现在使用入度时,1 2 3 为一组,4 5 为一组。


更改拓扑图后,结果正确


在此基础更改入度为出度




在此做个小总结。
首先,系统的一致性研究主要分为以下几个主要因素:
- 系统拓扑关系图
- 权重的设定
- 控制协议
- 输入时滞的影响
- 通信时滞的影响
在此基础上,搭建仿真模型,进行控制协议的验证。
通过以上几组实验对比,可基本得出时由于系统拓扑关系图不满足一致性要求所引起的。
书中所给的定理7.1,系统若想一致,需要满足以下三个条件:
-
基于入度平衡的假设条件(A1)和(A2);
-
当网络拓扑结构中包含全局可达节点时;
-
若满足 d ~ i ( α cos ( ω i 0 T i ) + β ω i 0 sin ( ω i 0 T i ) ) < 1 2 ω i 0 2 \tilde{d}_i(\alpha \cos(\omega_{i0} T_i) + \beta \omega_{i0} \sin(\omega_{i0} T_i)) < \frac{1}{2} \omega_{i0}^2 d~i(αcos(ωi0Ti)+βωi0sin(ωi0Ti))<21ωi02 成立,则称系统能渐进实现分组一致。
通过观察书中所给的系统拓扑关系图,均满足以上要求,并且未设置任何时滞,也一定满足条件(3)。
既然已经满足上述三个条件,但是还是不能收敛。接下来的实验,先验证之前搭建的系统模型没有问题,之后再研究拓扑图为什么不能收敛的问题。
之前的模型,将拓扑关系图更改之后,结果也都正常,包括节点分组情况也正确。
位置信息如下:

速度状态如下:
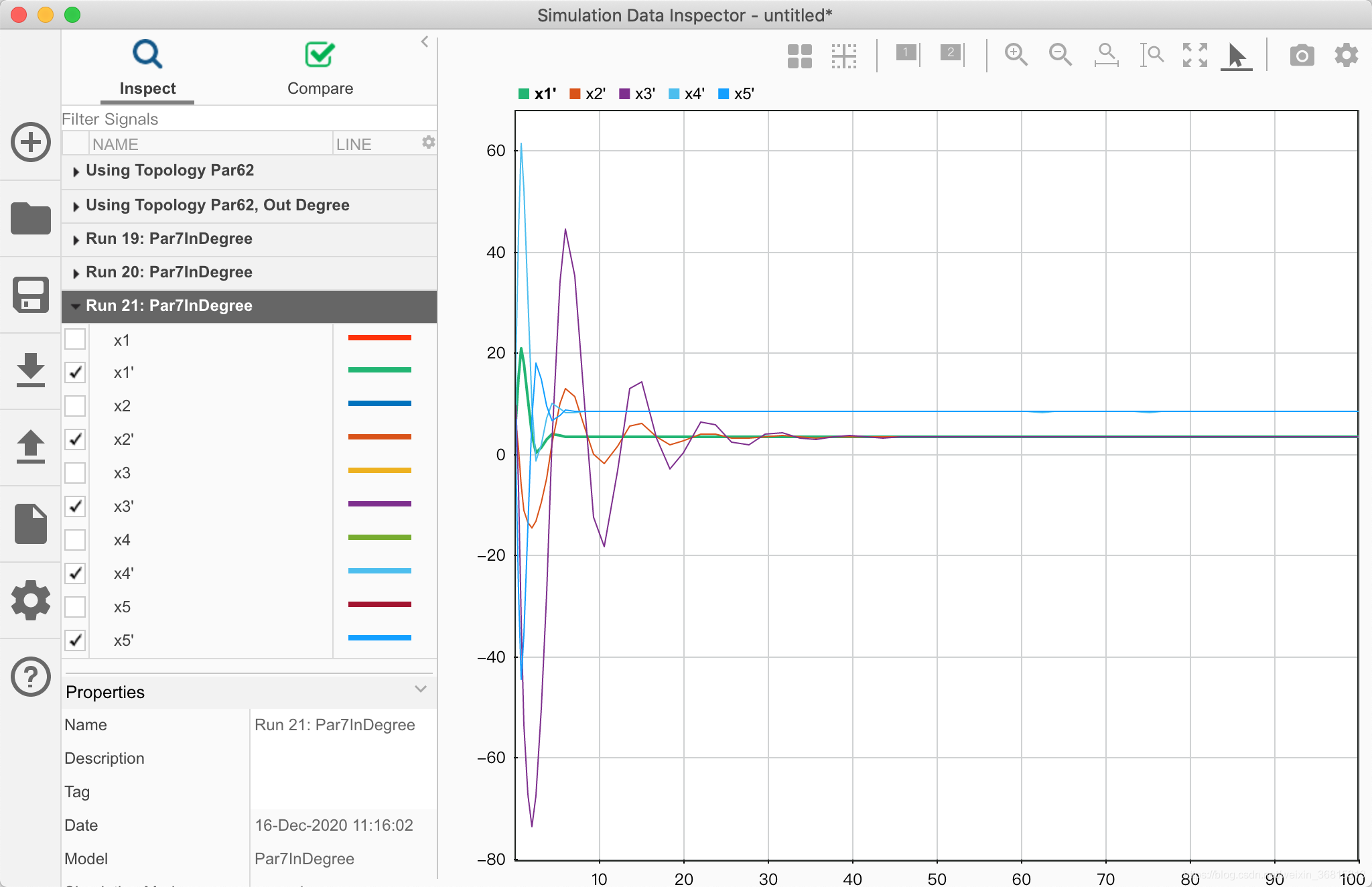
保持时滞为零,其他条件与采用第6章实验2所用拓扑图条件一致的情况下,仅更改为第7章拓扑图,还是无法收敛。算是再次验证了拓扑图是错误的。



























 822
822

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










