自抗扰控制


其中,e=v(t)-y(t)是控制系统参考输入量v(t)与被控对象输出量y(t)之间的差值,kp比例系数,ki积分系数,,kd微分系数
优点:
1.仅由误差来决定控制
2.运算量低,可以以极高的速率运行
缺点:
1.误差的取法e=v-y,使得初始时刻误差较大,容易造成控制系统快速性和超调的矛盾,比如输入为阶跃信号的时候,会导致误差函数也是一个阶跃信号,对控制系统的稳定性有影响。
2.实际中,参考输入量v(t)一般不可导,甚至不连续,并且y(t)中又常常存在噪声干扰,因而e(t)=v(t)-y(t)通常是不可导的,其微分信号难以利用,因而限制了PID控制器的应用。
3.经典pid的比列,误差,积分项是线性组合输出最后的控制量的,线性组合并不是一个最优的组合方案,常会引起系统快速性和超调量之间的矛盾
4.严格上说,积分项虽然消除了静态固有误差,但是会大大影响控制的稳定性能,积分反馈有许多副作用
针对上面的4个缺点,ADRC提出了改进方法
1.为了防止跳变信号,对信号作如下处理,就是用下面的微分跟踪器
u=−rsign(x1−v+x2|x2|2r)
如下图所示,使用这种变换实际上是模仿最短时间到达一个点的概念,在到达平衡处前恒定加速运动,过平衡位置后恒定减速运动,使目标点在规定的加速度下以最短的时间到达目标点,并且到达速度为0,其中v是当前位置
2. 微分器的改进
借助于高等数学有

或者由拉氏变换
即:采样周期越短,噪声被放大越大,因此采用如下改进:
问题:这里怎么证明噪声不被放大呢?

3. 非线性加权平均
其中v0为输入信号,目的是实现v1跟踪v0, v2跟踪到v1的导数,即间接实现v2跟踪到输入v0的导数,举例如下
有一个系统,其中输入信号为v0(t),













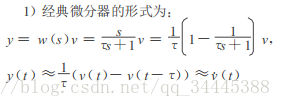

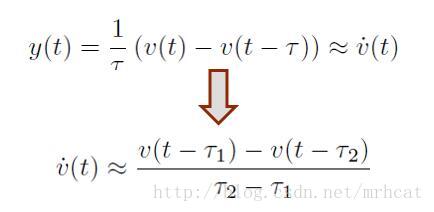














 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








