1、永磁同步电机的数学模型
在永磁同步电动机矢量控制系统中,常用的坐标系有两种:两相旋转坐标系( 坐标系)和两相静止坐标系(
坐标系)和两相静止坐标系(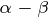 坐标系),各坐标系之间的关系如图所示,在图中永磁体产生的磁链矢量的方向和转子磁极的方向一致。
坐标系),各坐标系之间的关系如图所示,在图中永磁体产生的磁链矢量的方向和转子磁极的方向一致。
永磁同步电机是一个非线性系统,具有多变量、强耦合的特点。我们对其分析的时候有以下假设:
- 忽略铁芯饱和,不计涡流和磁滞损耗
- 忽略换相过程中的电枢反应
- 转子上无阻尼绕组,永磁体无阻尼作用
- 定子绕组电流在气隙中只产生正弦分布的磁势,无高次谐波
按照电动机应用建模
在此理想条件下:
1.1 永磁同步电机在三相静止坐标系下定子电压方程:
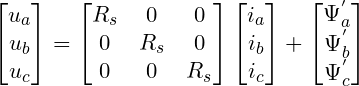
式中,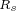 为电枢电阻,
为电枢电阻,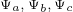 分别为
分别为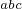 三相磁链,
三相磁链,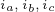 分别为其
分别为其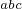 三相的相电流。
三相的相电流。
1.2 三相静止坐标系下磁链方程
其中,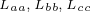 为各相绕组自感,且
为各相绕组自感,且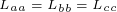 ,式中
,式中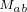 等为绕组之间互感且均相等。
等为绕组之间互感且均相等。 是永磁体磁链,
是永磁体磁链, 为转子
为转子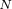 极和
极和 相轴线之间的夹角。
相轴线之间的夹角。
经过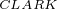 和
和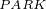 变换之后,得到其在
变换之后,得到其在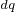 坐标系下的数学模型:
坐标系下的数学模型:
1.3  坐标系下电压方程
坐标系下电压方程
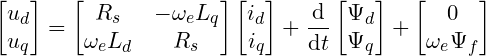
其中,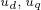 为
为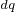 轴电压,
轴电压,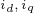 为
为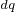 轴电流,
轴电流,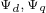 为
为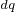 轴磁链,
轴磁链,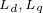 为
为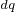 轴电感,
轴电感,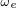 为转速。
为转速。
1.4  坐标系下磁链方程
坐标系下磁链方程
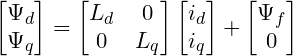
1.5 转矩方程
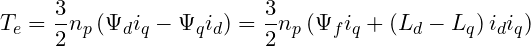
从上1.5中转矩方程可以看出,电磁转矩由两个部分组成。第一项是永磁体和定子绕组磁链之间相互作用产生,第二项则是由磁阻变化而产生的。这里我们需要区分一下凸极和隐极电机的区别,隐极电机由于 ,所以磁阻变化转矩是凸极电机特有的,我们在搭建仿真的时候也需要注意这里的电机类型。
,所以磁阻变化转矩是凸极电机特有的,我们在搭建仿真的时候也需要注意这里的电机类型。
小结:永磁同步电机的数学模型解释了其内部构成,有助于我们设计控制策略,我们进行坐标变换和PI参数整定时都需要对其数学模型进行分析。








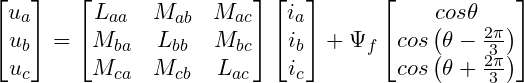
















 4963
4963

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








