这篇文章先不讲任何理论相关的东西,因为太多,后面十几篇文章慢慢讲,包括在语音信号处理、振动信号处理、心电信号出来及在引力波信号方面的应用,首先看一下前置文章
同步压缩变换初探 - 哥廷根数学学派的文章 - 知乎 同步压缩变换初探 - 知乎
再看连续小波变换 - 哥廷根数学学派的文章 - 知乎 再看连续小波变换 - 知乎
首先,给几个术语
FSST1: 标准同步压缩变换(一阶,基于短时傅里叶变换)standard synchrosqueezing
FSST2: 垂直二阶同步压缩变换vertical second-order synchrosqueezing
FSST3: 垂直三阶同步压缩变换vertical third-order synchrosqueezing
FSST4: 垂直四阶同步压缩变换vertical fourth-order synchrosqueezing
FRSTFT: 重排短时傅里叶变换reassigned STFT
FOSST: 倾斜同步压缩变换oblique synchrosqueezing
首先生成复信号
a1 = exp(2*(1-t).^3 + 1.5*t.^4);
a2 = 1+ 5*t.^3 + 7*(1-t).^6;
phi1 = 50*t+30*t.^3-20*(1-t).^4;
phi2 = 340*t-2.*exp(-2*(t-0.2)).*sin(14*pi.*(t-0.2));
if1 = 50+90*t.^2+80*(1-t).^3;
if2 = 340+4*exp(-2*(t-0.2)).*sin(14*pi.*(t-0.2))-28*pi.*exp(-2*(t-0.2)).*cos(14*pi.*(t-0.2));
s1 = a1.*exp(2*pi*1i*(phi1));
s2 = a2.*exp(2*pi*1i*(phi2));
s = s1+s2;看一下各个部分实虚部波形
FigHandle(1) = figure;
set(FigHandle(1),'units','normalized','outerposition',[0 0 1 1]);
plot(t, real(s1), 'm');
hold on; plot(t, a1, 'k', 'linewidth', 2) ;
legend('Re(f_1)','A_{1}','Location','south','Orientation','horizontal') ;
FigHandle(2) = figure;
set(FigHandle(2),'units','normalized','outerposition',[0 0 1 1]);
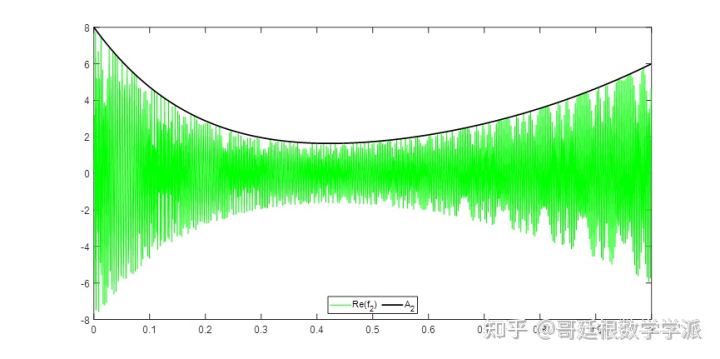
plot(t, real(s2), 'g');
hold on; plot(t, a2, 'k', 'linewidth', 2) ;
legend('Re(f_2)','A_{2}','Location','south','Orientation','horizontal') ;
FigHandle(3) = figure;
set(FigHandle(3),'units','normalized','outerposition',[0 0 1 1]);
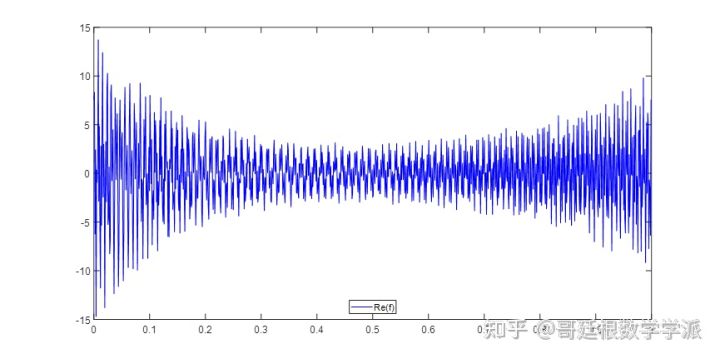
plot(t, real(s), 'b') ;
legend('Re(f)','Location','south') ; 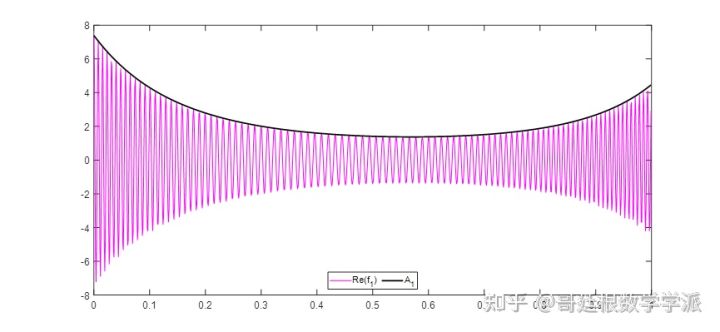
看一下几种同步压缩方法的时频谱压缩效果
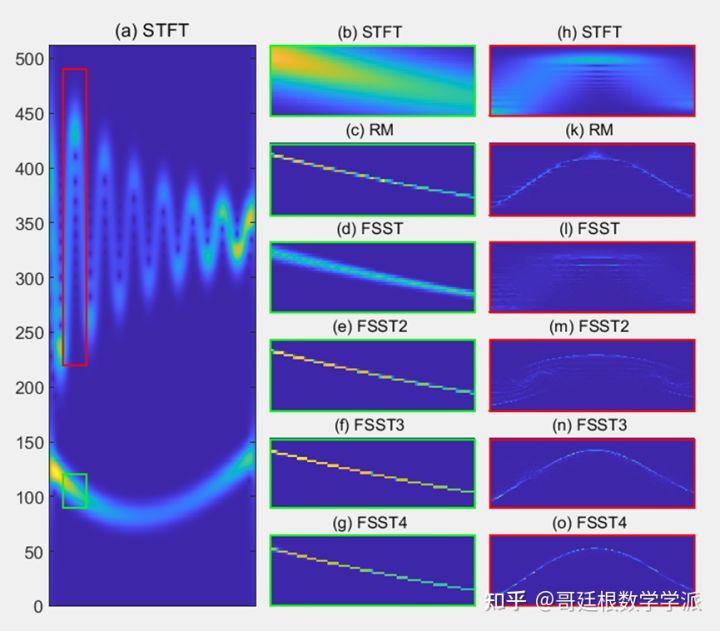
不同噪声水平下同步压缩的效果
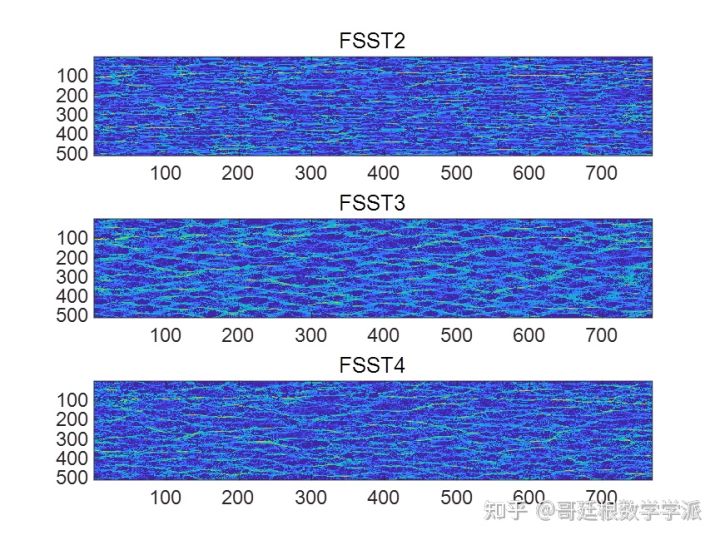
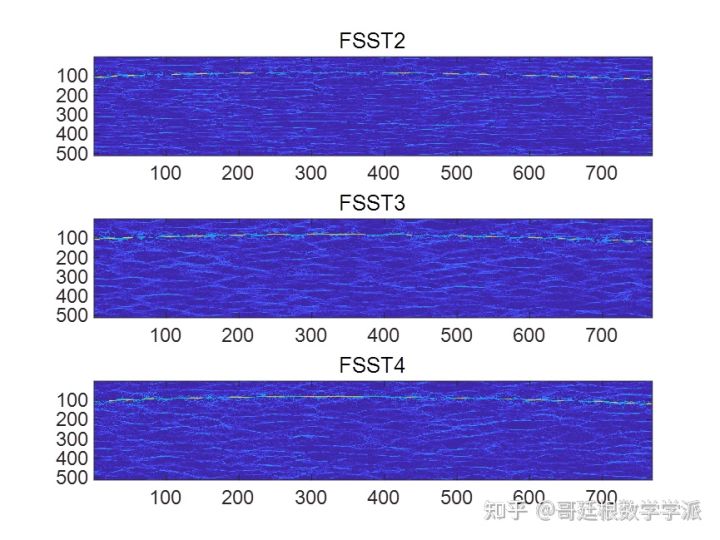
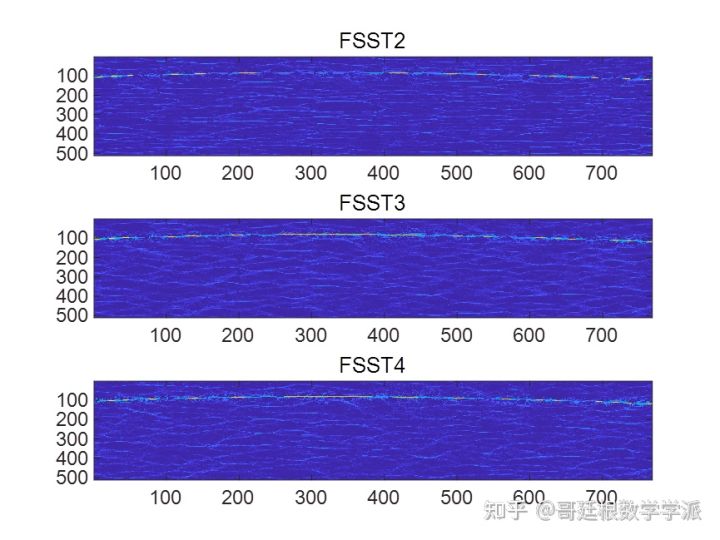
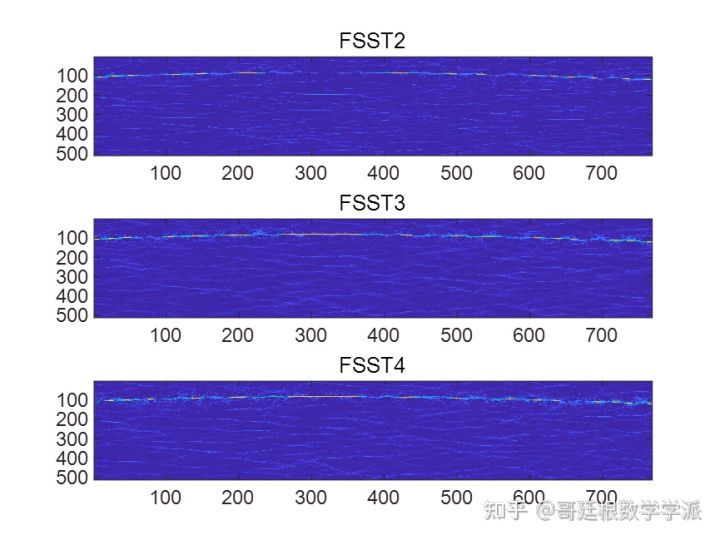
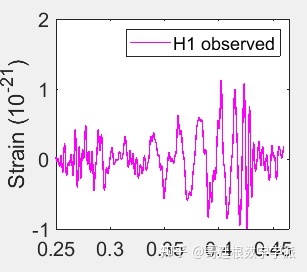
看看引力波波形
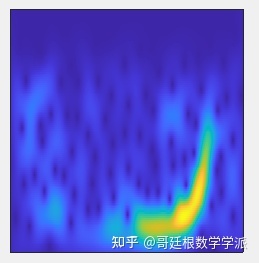
STFT时频谱
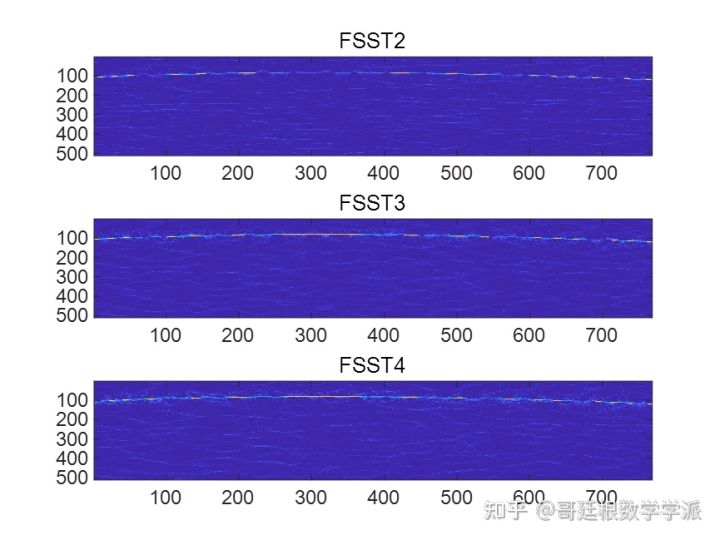
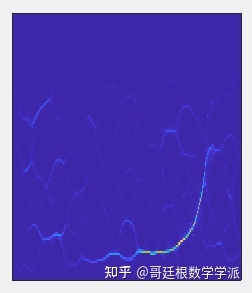
FSST2时频谱
FSST3时频谱
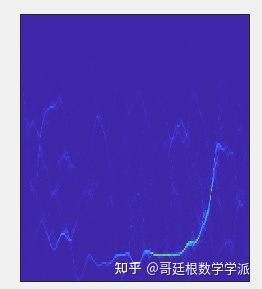
FSST4时频脊线提取
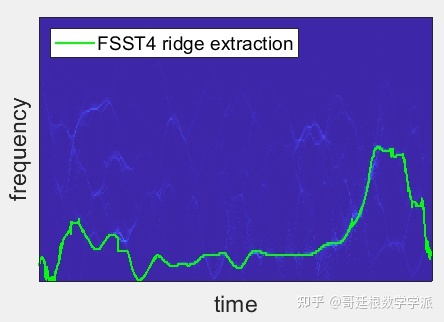








 本文探讨了同步压缩变换在语音、振动、心电及引力波信号处理中的应用,介绍了FSST和FOSST等不同阶数的同步压缩变换,并通过实例展示了它们在时频谱压缩和噪声水平变化下的效果。此外,还对比了STFT、FSST2至FSST4的时频谱特征,特别关注了引力波信号的解析能力。
本文探讨了同步压缩变换在语音、振动、心电及引力波信号处理中的应用,介绍了FSST和FOSST等不同阶数的同步压缩变换,并通过实例展示了它们在时频谱压缩和噪声水平变化下的效果。此外,还对比了STFT、FSST2至FSST4的时频谱特征,特别关注了引力波信号的解析能力。

















 1462
1462

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










