测度定义_B-S模型下的PDE和风险中性测度方法

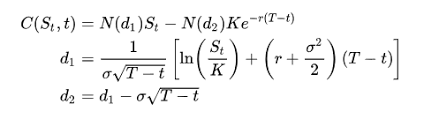
本篇将解决Black Scholes公式的求解方法。在上一篇文章

呦呦Ruming：From Brownian Motion to Stochastic Integral​zhuanlan.zhihu.com

中我们介绍了布朗运动与伊藤公式，通过这些数学公式我们将推导Black-Scholes估值公式。

Part 1. 利用资产组合对冲期权

在此部分我们将通过偏微分方程的方法来求解BS公式，这种方法的核心思想与之前离散情况下二叉树模型是类似的，即构造一个资产组合使得到期时能够完全对冲期权的风险，再通过资产组合的价格来对期权进行定价。（对冲策略的构造，可见

呦呦Ruming：美式期权的对冲​zhuanlan.zhihu.com

def 1.1 （广义几何布朗运动）假设有W(t)，

，是一个布朗运动，

是其对应的域流，假设

是适应的随机过程，定义一个Ito过程X(t)，其满足：

容易知道