目录
一、相机中的坐标:

相机坐标中有4个坐标系(右手系),为world、camera、image、pixel
- 世界坐标系(World):真是存在或者不存在的点,可以任意指定;
- 相机坐标系(Camera):原点为相机针孔,z与光轴重合,
和
平行投影面;
- 图像坐标系(Image):原点为光轴和投影面的焦点,
和
平行投影面;
- 像素坐标系(Pixel):投影面坐上角为
,u,v和投影两个边重合;
二、内参公式推导:

设置图像中点P坐标为:
在物理成像平面坐标为:
因为小孔成像为相似三角形,所以可以得到:
;

将成像平面转移到以小孔划分的物一侧:
进一步可得:
,
设图像的像素坐标P'为:
若坐标在u上缩放了倍,在v上缩放了
倍,同时平移了
那么在图像上P‘表示为:
将,
代入到:
并定义:
得:
那么可以得出:
若相机的世界坐标为,那么:
三、坐标系的转换:
1.世界坐标系 到 相机坐标系
世界坐标系中有一点:
相机坐标系中有一点:
可得:
其中:
2.相机坐标系 到 图像坐标系
相机坐标系中有一点:
图像坐标系中有一点:
根据小孔成像原理:
,
所以:
补全成其次方程可得:
可得:
即:
实际中主点可能不再图像坐标原点,若点在坐标系中的坐标为
那么:
3.图像坐标系 到 像素坐标系
设像素坐标为:
设图像坐标为:
一个像素的长和宽为:
那么:
改写为矩阵:
即:
因为:
所以结合相机到图像的变换,那么相机到像素的变换矩阵为:
4.世界坐标系 到 像素坐标系
根据以上可得:
即:
四、相机畸变:
1.径向畸变(透镜自身形状对光线的影响)
- 桶形畸变
- 枕形畸变

可以通过三个畸变参数来纠正,其中畸变较小的图像中心区域可以用
来纠正,越向边缘走依次用
:
2.切向畸变(机械组装偏差)

使用 来纠正
3.通过5个参数来纠正畸变
设归一化坐标为
通过8个参数来纠正畸变:
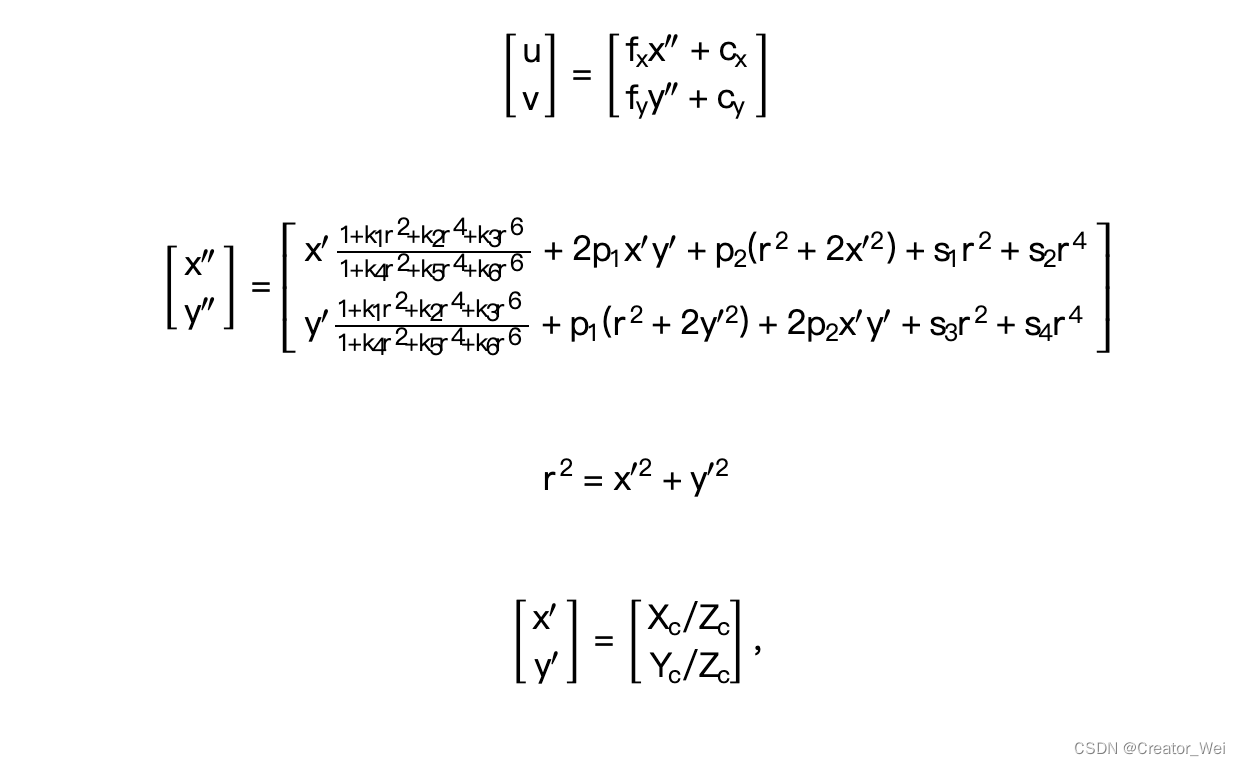
五、双目相机模型:

根据相似三角形原理:
可得:
其中






















 783
783











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








