【Apollo Common代码解析-vetor向量相关】

在看apollo的common的代码，发现大量运用了向量的相关知识，就整理了一些向量的一些基础内容。主要是参考了百度百科和下面的博客。
参考文献：
[1] https://zhuanlan.zhihu.com/p/143222979
[2]百度百科
[3]《数学要素》姜伟生
[4]apollo源码

1.1 向量的定义

百度的定义：在数学中，向量（也称为欧几里得向量、几何向量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。如图1所示，线段的长度表示向量的大小，向量的方向也就是箭头所指的方向。
n个有次序的数$$x_1,x_2,x_3......x_n$$所组成的数组称为n维向量，这个数称为该向量的个分量，第i个数称为第个分量。向量的大小称为模长。
n维向量可以写成一行，称为行向量；n维向量写成一列，称为列向量。

行向量的下标一般是1xN,1 × N 代表“1 行、N列”，N × 1 代表“N 行、1 列”；
利用 NumPy 库，可以用 numpy.array([[1, 2, 3,…n]]) 定义行向量。用numpy.array([[1], [2], [3],…[n]) 定义 列向量。
注意，定义向量时如果只用一层中括号 []，比如 numpy.array([1, 2, 3])，得到的结果只有一个维度；有两层中括号 [[]]，numpy.array([[1, 2, 3]]) 得到的结果有两个维度。
向量中也有反向量、零向量、等向量等。若一个向量与它的大小相同，但方向相反，则称它为反向量，一般记作$-\vec{v}$。若一个向量的始点与终点重合，也就是重合点的向量，即$\vec{0}=\overrightarrow{AA}=\overrightarrow{BB}$，则称它为零向量。零向量具有方向性，但方向不定。若两个向量长度、方向相等，即为等向量。规定长度为1的向量为单位向量，可以把一个非零向量归一化为一个单位向量，如等式所示:

对于坐标系中的两个点$A(x_0,y_0),B(x_1,y_1)$组成的向量$\overrightarrow{AB}=(x_1-x_0,y_1-y_0)$,同理得：$\overrightarrow{BA}=(x_0-x_1,y_0-y_1)$
行向量转置 (transpose) 得到列向量；同理，列向量转置得到行向量。

1.2 向量的运算

1.2.1 向量相加减

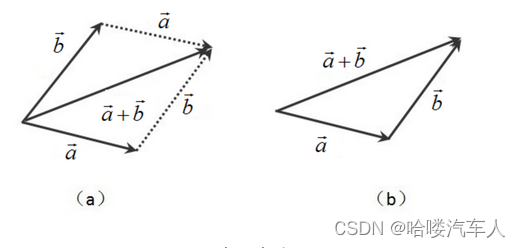
向量的加法满足平行四边形法则和三角形法则。具体地，两个矢量和相加，得到的是另一个向量。这个向量可以表示为和的起点重合后，以它们为邻边构成的平行四边形的一条对角线，或者表示为将的终点和的起点重合后，从的起点指向的终点的向量，如图2所示，图（a）是平行四边法法则，图（b）是三角形法则。

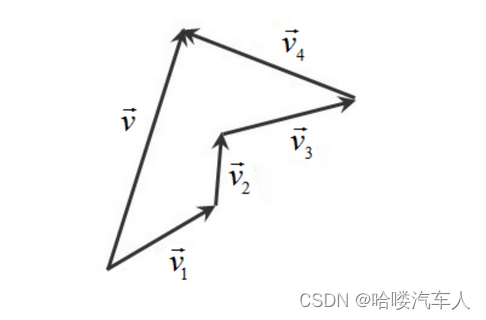
当多个向量相加时，例如求个k向量$\overrightarrow{v_1},\overrightarrow{v_2},\overrightarrow{v_3},...,\overrightarrow{v_k}$相加得到的向量，这个向量可以表示为将第i(i<k)个向量的起点和第(i+1)个向量的终点重合后，从$\overrightarrow{v_1}$的起点指向$\overrightarrow{v_1},\overrightarrow{v_2},\overrightarrow{v_3},...,\overrightarrow{v_k}$的终点的向量，如图3所示。

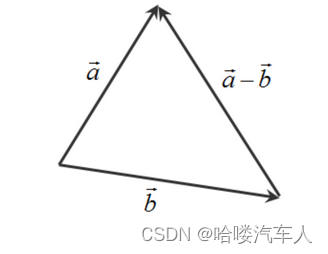
两个向量$\vec{a}$和$\vec{b}$的相减，则可以看成是向量$\vec{a}$加上一个与$\vec{b}$大小相等，方向相反的向量。或者，$\vec{a}$和$\vec{b}$的相减得到的向量可以表示为$\vec{a}$和$\vec{b}$的起点重合后，从$\vec{b}$的终点指向$\vec{a}$的终点的向量，如图4所示。

如果用坐标表示向量的加减如下：

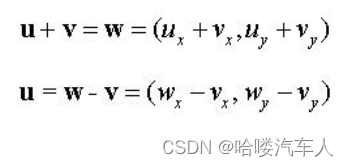
1.2.2向量与数相乘

向量与数相乘相当于向量的重复相加，一个标量k和一个向量$\vec{v}$之间可以做乘法，得出的结果是另一个与$\vec{v}$方向相同或相反，大小是$\vec{v}$的大小的|k|倍的向量，可以记成$k\vec{v}$，实际上就是k个$\vec{v}$相加。-1乘以任意向量会得到它的反向量，0乘以任何向量都会得到零矢量。如图5所示，对5个(2, 1)向量求和，得到的向量如下：

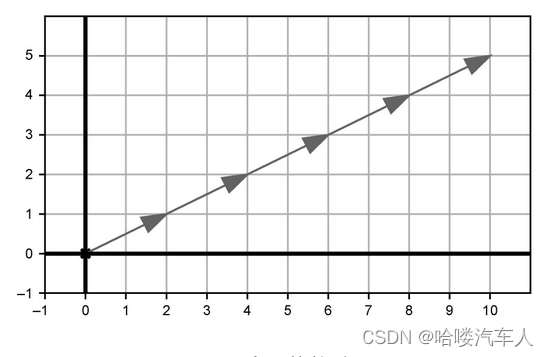
1.2.3 点积运算

定义：已知两个非零向量$\vec{a}.\vec{b}$，作OA=a,OB=b，则∠AOB称作向量a和向量b的夹角，记作θ并规定0≤θ≤π
定义：两个向量的数量积（内积、点积）是一个数量（没有方向），记作a·b。

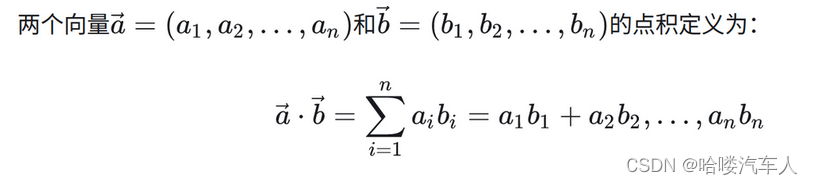
这里要求一维向量a和向量b的行列数相同。
从几何的角度理解内积，两个向量的内积几何意义是投影

特别地，0·a =a·0 = 0；若a，b是非零向量，则a与b正交(垂直)的充要条件是a·b = 0。
点乘的结果是一个数,，比如下图A . B的值为向量A在向量B方向上的投影。

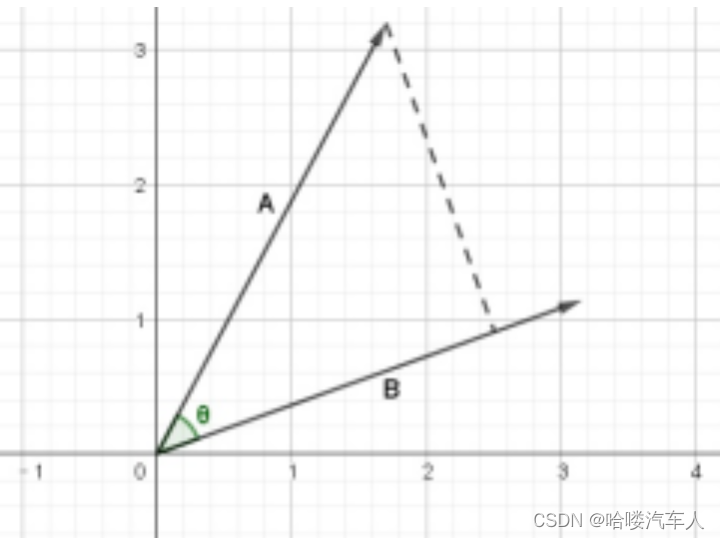
向量的点乘的应用

向量的点乘可以用来计算两个向量之间的夹角，进一步判断这两个向量是否正交（垂直）等方向关系。同时，还可以用来计算一个向量在另一个向量方向上的投影长度。
点乘的应用主要有计算角度、计算面积、检测正交性。计算角度的公式如下：

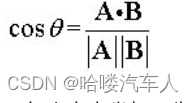
计算面积例如：求任给多边形的面积，多边形给出了每个定点坐标，先把所有的多边形分解成多个三角形，然后只要能求出三角形面积，问题就解决了。
其次是判断两个向量是否同一方向或正交(即垂直)等方向关系，具体对应关系为：
a∙b>0→方向基本相同，夹角在0°到90°之间
a∙b=0→ 正交，相互垂直
a∙b<0→ 方向基本相反，夹角在90°到180°之间

1.2.3 叉乘运算

定义：两个向量a和b的向量积（外积、叉积）是一个向量，记作a×b（这里“×”并不是乘号，只是一种表示方法，与“·”不同，也可记做“∧”）。若a、b不共线，则a×b的模是：∣a×b∣=|a||b|·sin〈a，b〉；a×b的方向是：垂直于a和b，且a、b和a×b按这个次序构成右手系。若a、b垂直，则∣a×b∣=|a||b|（此处与数量积不同，请注意），若a×b=0，则a、b平行。叉乘运算结果是一个向量而不是一个标量，向量积即两个不共线非零向量所在平面的一组法向量，并且两个向量的外积与这两个向量组成的坐标平面垂直。
向量$\vec{a}$和$\vec{b}$的外积$\vec{a}$x$\vec{b}$是一个向量，其长度等于|a||b|sin∠(a,b)，其方向正交于a与b。并且，($\vec{a}$,$\vec{b}$,$\vec{a}$x$\vec{b}$) 构成右手系。特别地，0×a = a×0 = 0.此外，对任意向量a，a×a=0。
对于二维向量来说，叉积的定义是：

二维向量叉积是一种特殊情况，它的结果是一个标量而非向量，从几何上定义为：

其中，$\theta$表示向量$\vec{a}$和$\vec{b}$之间逆时针方向的夹角大小。因此，二维向量叉积的结果是以和为边的平行四边形的面积，如图所示。叉积的顺序影响结果的正负号，如果置换叉积的顺序，即，那么结果是一个负数。

向量a×向量b（×为向量叉乘），若结果小于0，表示向量b在向量a的顺时针方向；若结果大于0，表示向量b在向量a的逆时针方向；若等于0，表示向量a与向量b平行。（顺逆时针是指两向量平移至起点相连，从某个方向旋转到另一个向量小于180度）。

1.2.4 点乘叉乘的具体应用及面试题

这部分是我以前面试遇到的题目，基本上都是与向量的运算相关，大致记录一下，后面到apollo中的 LineSegment2d有具体计算原理。
1.4.1 点乘和叉乘的定义及区别是什么

1.4.2 计算点到线段的最小距离

1.4.3判断点是否在线段上

1.4.4 判断线段是否相交

1.4.5 判断点是否在矩形内部

1.4.6 判断点在线段的哪一侧
给出三个点A（x1,y1）、B（x2,y2）、P（x0,y0），判断P点在线段AB的哪一侧。
如上图所示，向量AB与向量AP叉乘得到的向量是垂直面ABP，根据右手准则可得P点在AB右侧：
AB=(x2-x1,y2-y1);
AP=(x0-x1,y0-y1);
AB x AP=(x2-x1)(y0-y1)-(y2-y1_)(x0-x1)
如果AB x AP小于0则说明P点在AB的右侧，大于0说明在左侧。

1.3 Apollo vec_2d代码

代码注释较为详细。

/******************************************************************************
 * Copyright 2017 The Apollo Authors. All Rights Reserved.
 *
 * Licensed under the Apache License, Version 2.0 (the "License");
 * you may not use this file except in compliance with the License.
 * You may obtain a copy of the License at
 *
 * http://www.apache.org/licenses/LICENSE-2.0
 *
 * Unless required by applicable law or agreed to in writing, software
 * distributed under the License is distributed on an "AS IS" BASIS,
 * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
 * See the License for the specific language governing permissions and
 * limitations under the License.
 *****************************************************************************/

/**
 * @file
 * @brief Defines the Vec2d class.
 */

#pragma once

#include <cmath>
#include <string>

/**
 * @namespace planner::common::math
 * @brief planner::common::math
 */
namespace planner
{
  namespace common
  {
    namespace math
    {

      constexpr double kMathEpsilon = 1e-10;

      /**
       * @class Vec2d
       *
       * @brief Implements a class of 2-dimensional vectors.
       */
      class Vec2d
      {
      public:
        //! Constructor which takes x- and y-coordinates.
        constexpr Vec2d(const double x, const double y) noexcept : x_(x), y_(y) {}

        //! Constructor returning the zero vector.
        constexpr Vec2d() noexcept : Vec2d(0, 0) {}

        //! Creates a unit-vector with a given angle to the positive x semi-axis创建与正x半轴成给定角度的单位向量
        static Vec2d CreateUnitVec2d(const double angle);

        //! Getter for x component
        double x() const { return x_; }

        //! Getter for y component
        double y() const { return y_; }

        //! Setter for x component
        void set_x(const double x) { x_ = x; }

        //! Setter for y component
        void set_y(const double y) { y_ = y; }

        //! Gets the length of the vector
        double Length() const;

        //! Gets the squared length of the vector获取向量长度的平方
        double LengthSquare() const;

        //! Gets the angle between the vector and the positive x semi-axis获取向量和正x半轴之间的角度
        double Angle() const;

        //! Returns the unit vector that is co-linear with this vector返回与此向量共线的单位向量
        void Normalize();

        //! Returns the distance to the given vector
        double DistanceTo(const Vec2d &other) const;

        //! Returns the squared distance to the given vector
        double DistanceSquareTo(const Vec2d &other) const;

        //! Returns the "cross" product between these two Vec2d (non-standard).二维向量的叉乘。
        double CrossProd(const Vec2d &other) const;

        //! Returns the inner product between these two Vec2d.二维向量的内积。
        double InnerProd(const Vec2d &other) const;

        //! rotate the vector by angle.向量旋转一定角度之后得到一个新向量
        Vec2d rotate(const double angle) const;

        //! rotate the vector itself by angle.按角度旋转向量本身
        void SelfRotate(const double angle);

        //! Sums two Vec2d
        Vec2d operator+(const Vec2d &other) const;

        //! Subtracts two Vec2d
        Vec2d operator-(const Vec2d &other) const;

        //! Multiplies Vec2d by a scalar
        Vec2d operator*(const double ratio) const;

        //! Divides Vec2d by a scalar
        Vec2d operator/(const double ratio) const;

        //! Sums another Vec2d to the current one
        Vec2d &operator+=(const Vec2d &other);

        //! Subtracts another Vec2d to the current one
        Vec2d &operator-=(const Vec2d &other);

        //! Multiplies this Vec2d by a scalar
        Vec2d &operator*=(const double ratio);

        //! Divides this Vec2d by a scalar
        Vec2d &operator/=(const double ratio);

        //! Compares two Vec2d
        bool operator==(const Vec2d &other) const;

        //! Returns a human-readable string representing this object
        std::string DebugString() const;

      protected:
        double x_ = 0.0;
        double y_ = 0.0;
      };

      //! Multiplies the given Vec2d by a given scalar将给定的Vec2d乘以给定的标量，向量的数乘
      Vec2d operator*(const double ratio, const Vec2d &vec);

    } // namespace math
  }   // namespace common
} // namespace apollo

代码相对容易理解，不展开说明了。
我新增了两个函数
一个是计算与另外一个有向线段的夹角，一个是计算一个点绕另外一个点旋转的一定角度得到的新坐标，角度为正时候是逆时针旋转。

  void Vec2d::rotate_coord_of_point(const Vec2d &point, const double &theta, Vec2d &NewPoint)
      {
        NewPoint.set_x(x_ + (point.x() - x_) * cos(theta) - (point.y() - y_) * sin(theta));
        NewPoint.set_y(y_ + (point.x() - x_) * sin(theta) + (point.y() - y_) * cos(theta));
      }
      double Vec2d::AngleTo(const Vec2d &other) const
      {
        return acos(InnerProd(other) / (Length() * other.Length()));
      }