【基础函数-圆相关】

在apollo的common中没有圆相关的计算，而在路径规划领域圆相关的计算也有一些应用，尤其是泊车规划，目前整理了一些基本的公式使用。

基本定义

定一个圆为圆心坐标和半径r

class Circle
{
  private:
  double x_;
  double y_;
  double r_;
  Circle() : x_(0), y_(0), r_(0) {}
  Circle(double a, double b, double c) : x_(a), y_(b), r_(c) {}
}

圆的方程有一般式和标准式：
x2+y2+Dx+Ey+F=0, (D2+E2-4F>0)，或可以表示为
$$(x+D/2{)}^2+(x+E/2{)}^2=(D^2+E^2-4F)/4$$
如果(1)圆半径长r；(2)中心A的坐标(a,b)，标准方程就是：
$$(x-a{)}^2+(y-b{)}^2=r^2$$

三点确定一个圆心

设圆心坐标O为 $(x_0,y_0)$，半径为r,三个点的坐标分别是，A$(x_1,y_1)$，B $(x_2,y_2)$)，C $(x_3,y_3)$
根据三个点到圆心的距离相等：

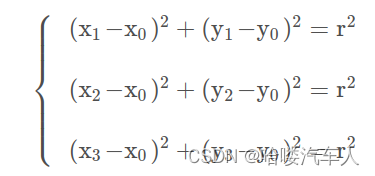
化简可以得到：

其中：

此处参考：三点定圆推导公式
首先判断三点是否共线，如果共线则不存在圆

 bool Circle::CalCircle(const Vec2d &pt1, const Vec2d &pt2, const Vec2d &pt3, Vec2d &center)
            {
                if (Line::ThreePointsIsCollinear(pt1, pt2, pt3))
                {
                    return false;
                }
                double a = pt1.x() - pt2.x();
                double b = pt1.y() - pt2.y();
                double c = pt1.x() - pt3.x();
                double d = pt1.y() - pt3.y();
                double e = ((pt1.x() * pt1.x() - pt2.x() * pt2.x()) - (pt2.y() * pt2.y() - pt1.y() * pt1.y())) / 2;
                double f = ((pt1.x() * pt1.x() - pt3.x() * pt3.x()) - (pt3.y() * pt3.y() - pt1.y() * pt1.y())) / 2;

                // 圆心位置
                double x = (e * d - b * f) / (a * d - b * c);
                double y = (a * f - e * c) / (a * d - b * c);
                center.set_x(x);
                center.set_y(y);
                r_ = center.DistanceTo(pt1);
                center_ = center;
                return true;
            }

计算两个圆的位置关系并且求出交点

利用圆心距与两圆半径之间的关系来判断两圆的位置关系。假设 d c dc dc为圆心距, R R R与 r r r分别是两圆的半径，则：
（1） dc>R+r，两圆外离；
（2） dc=R+r，两圆外切；
（3） |R – r|< d c < |R + r| ，两圆相交；
（4） dc = |R – r| ，两圆内切；
（5） 0 < = d c < |R – r| ，两圆内含。

 // 两个圆的位置关系存在五种，分别是外离，外切，相交，内切，内含分别对应12345；
            int Circle::PosRelationToOtherCircle(const Circle &other_circle, Vec2d &p1, Vec2d &p2)
            {
                double dis = center_.DistanceTo(other_circle.center_);
                double r1 = r_;
                double r2 = other_circle.r();
                if (dis - (r1 + r2) > 0)
                {
                    // std::cout << "两圆外离" << endl;
                    return 1;
                }
                else if (dis == (r1 + r2))
                {
                    IntersectionToCircle(other_circle, p1, p2);
                    //  cout << "两圆外切" << endl;
                    return 2;
                }
                else if ((fabs(r1 - r2) - dis < 0) && (dis - (r1 + r2) < 0))
                {
                    IntersectionToCircle(other_circle, p1, p2);
                    // cout << "两圆相交" << endl;
                    return 3;
                }
                else if (dis == abs(r1 - r2))
                {
                    IntersectionToCircle(other_circle, p1, p2);
                    //  cout << "两圆内切" << endl;
                    return 4;
                }
                else
                {
                    // cout << "两圆内含" << endl;
                    return 4;
                }
            }

圆与圆的交点计算后续补充。

圆与直线的位置关系及交点计算

假设直线方程和圆的方程为：
$$y=kx+c$$
$$(x-a{)}^2+(y-b{)}^2=r^2$$
联立两个方程可以得到：
$$(1+k^2)x^2+x[2k(c-b)-2a]+a^2+(c-b{)}^2-r^2=0$$
这里主要是使用圆的方程和直线方程联合求解，得到一个一元二次方程，这个二次方程的解就是交点坐标的x值。

  // calculate intersection point of a line and a circle
 // return 0 无交点，1.一个交点，2是两个交点
            int Circle::IntersecLine(const Line &line, Vec2d &p0, Vec2d &p1)
            {
                // get known line A B C
                float A, B, C;
                A = line.A_;
                B = line.B_;
                C = line.C_;
                float x0, x1, y0, y1;
                // calculate intersection
                float k, b, AA, BB, CC;
                int nRet = 0;
                if (fabs(A) < kMathEpsilon && fabs(B) < kMathEpsilon)
                {
                    return 0;
                }
                if (fabs(B) > kMathEpsilon)
                {
                    k = -A / B;
                    b = -C / B;
                    AA = 1 + k * k;
                    BB = 2 * (k * b - x_ - k * y_);
                    CC = pow(x_, 2) + pow((b - y_), 2) - r_ * r_;
                    if (SolveEquation::QuadraticEquation(AA, BB, CC, x0, x1))
                    {
                        y0 = k * x0 + b;
                        y1 = k * x1 + b;
                        nRet = 2;
                    }
                }
                else
                {
                    b = -C / A;
                    x0 = b;
                    x1 = b;
                    if (pow(r_, 2) >= pow(x_ - b, 2))
                    {
                        nRet = 2;
                        y0 = sqrt(r_ * r_ - pow((x_ - b), 2)) + y_;
                        y1 = y_ - sqrt(r_ * r_ - pow((x_ - b), 2));
                    }
                    else
                    {
                        nRet = 0;
                    }
                }
                if (nRet != 0)
                {
                    p0.set_x(x0);
                    p0.set_x(y0);
                    p1.set_x(x1);
                    p1.set_x(y1);
                }
                return nRet;
            }

已知两直线，求其相切圆

已经知道两条直线的方程L0,L1,求与其相切的圆的坐标，半径（已知）。
后续补充。

已知两个点在圆上，求两圆相切时的半径

针对平行车位(右侧车位，左侧车位转到右侧计算)来说，常见的场景如下图所示：

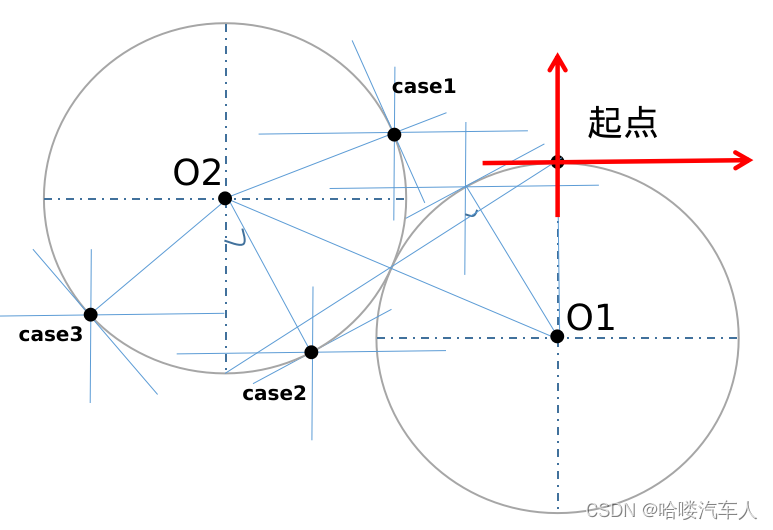
左侧的为入库点，可能存在情况基本为如图所示的三种，而这三种case计算圆心坐标的方式只有一种：
$$O_1.x=0;O_1.y=-r;O_2.x=x_1-r\ast sin(\theta );O_2.y=y_1+r\ast cos(\theta );$$
其中x1,y1是新坐标系下的目标点的坐标。
那么可以列方程：两圆心之间的距离=2*r;
这样可以得到一个一元二次方程。

double a = sin(t1) * sin(t1) + (1 + cos(t1)) * (1 + cos(t1)) - 4;
double b = -2 * sin(t1) * x1 + 2 * (1 + cos(t1)) * y1;
double c = x1 * x1 + y1 * y1;

求出半径即可。

以上为个人学习使用，请批评指正，如有侵权，请联系删除。

参考文献

【1】https://blog.csdn.net/qq_45874328/article/details/114934147