【论文阅读】Optimal Auctions Through Deep Learning

【论文阅读】Optimal Auctions Through Deep Learning

0 背景调研

本文发表在 PMLR-2019 中，目前被引次数为 155 次（谷歌学术）。

第一作者：Paul David Dütting

http://paulduetting.com/

第二作者：Zhe Feng

https://zfengharvard.github.io/

第三作者：Harikrishna Narasimhan

https://hari-research.github.io/

第四作者： David C. Parkes

https://parkes.seas.harvard.edu/

一作在读博期间访问过四作，二作是四作的博士导师。

第五作者：Sai S. Ravindranath

四作是五作的博士导师。

1 本文解决了什么问题？

最优拍卖设计是经济学理论的基石之一，具有较强的现实意义。在标准的独立私有估值模型中，每个竞标者都有一个关于拍卖物品的子集的估值函数，该函数独立于不一定相同的分布。拍卖师知道价值分布，但不知道出价人的实际估价（支付意愿）。如果投标人觉得有可图，则可以选择采取策略性的动作，不如实汇报估价。规避这一问题的一种方法是要求每个竞标者如实报告其估价，这符合每个竞标者的最大利益。本文的目标是学习一种激励相容的拍卖方式，使收益最大化。

在过去的工作中，Myerson 解决了单物品的最优拍卖机制设计的问题，而多物品的最优拍卖机制设计仍没有被完美解决。现有的针对多物品的最优拍卖机制设计的算法程序都只适用于 较弱的贝叶斯激励相容（Bayesian incentive compat- ibility (BIC)），而本文聚焦于设计一个满足 占优策略激励相容（dominant- strategy incentive compatibility (DSIC)） 的拍卖，这是一个强有力的概念。

补充：贝叶斯激励相容和占优策略激励相容

来源：https://zhuanlan.zhihu.com/p/420273236

本文提供了 第一个、通用的、端到端的 方法以解决多物品拍卖机制设计问题。本文使用多层神经网络对拍卖机制进行编码，投标人的估价作为输入，分配和支付决策作为输出。然后，使用来自价值分布的样本训练网络，以便在激励相容约束下最大化期望收益。

2 本文提出的解决方法是什么？

2.1 拍卖设计作为一个学习问题

基本知识

作者考虑一个含有 $n$ 个竞标者的集合 N = { 1 , … , n } N=\{1, \ldots, n\} N={1,…,n} 和 $m$ 个物品的集合 M = { 1 , … , m } M=\{1, \ldots, m\} M={1,…,m} 的设置。每个竞标者 $i$ 都有一个估值函数 $v_i:2^M\to {\mathbb{R}}_{\ge 0}$，其中 $v_i(S)$ 表示竞标者 $i$ 对物品子集 $S\subseteq M$ 的估值。在最简单的情况下，竞标者可能有 加性估值，他对 $M$ 中的个别项目都有估值，则对 $S\subseteq M$ 的估值为： v i ( S ) = ∑ j ∈ S v i ( { j } ) v_{i}(S)=\sum_{j \in S} v_{i}(\{j\}) vi​(S)=∑j∈S​vi​({j})。竞标者 $i$ 的估值函数独立于可能估值函数 $V_i$ 上的分布 $F_i$。本文使用 $v=\left(v_1,\dots ,v_n\right)$ 表示估值函数的概要，并写为 $V={\prod }_{i=1}^n{V}_i$ 。

拍卖师知道分布 $F=(F1，\dots ，F_n)$，但不知道竞标者的实际估值 $v$。竞标者报告他们的估价（可能是不真实的），拍卖机制决定如何给竞标者分配物品，并向他们收取费用。本文将一次拍卖 $(g,p)$ 表示为一对 分配规则 $g_i:V\to 2^M$ 和 支付规则 $p_i:V\to {\mathbb{R}}_{\ge 0}$。给定出价 $b=(b1，\dots ，bn)\in V$，拍卖计算分配 $g(b)$ 和支付 $p(b)$。

估价为 $v_i$ 的竞标者接收到一个 效用（utility）$u_i(v_i,b)=v_i(g_i(b))-p_i(b)$，用于提交投标概况 $b$。竞标者是具有策略的，以最大化他们自己的效用，并可能报告的出价与他们的估值不相同（说谎）。令 $v_{-i}$ 表示不含 $v_i$ 的估值概要 $v=(v1，\dots ，vn)$；对 $b_{-i}$ 也是如此，并且令 $V_{-i}={\prod }_{j\ne i}{V}_j$ 表示竞标者 $i$ 以外的竞标者可能的估值概要。

如果每个竞标者的效用最大化是无论其他竞标者如何报告，都如实报告自己的估值，则 该拍卖是 占优策略激励兼容（DSIC） 的。换句话说，对于每个投标人 $i$，每个估值$v_i\in V_i$，每个投标（出价） $b_i\in V_i$，以及所有来自他人的投标 $b_{-i}\in V_{-i}$，有 $u_i\left(v_i,\left(v_i,b_{-i}\right)\right)\ge u_i\left(v_i,\left(b_i,b_{-i}\right)\right)$ 成立。

在 DSIC 拍卖中，每个竞标者如实出价是最符合其利益的，因此估值概况 $v$ 的收入为 ${\sum }_i{p}_i(v)$。最优拍卖设计旨在确定一种 DSIC 拍卖，使预期收益最大化。

定义为学习问题

本文将最优拍卖设计的问题定义为一个学习问题。其中，在衡量目标标签误差的损失函数上，本文采用对 $F$ 上采样出的估价的负期望收益。本文给出了拍卖的参数类 $\left(g^w,p^w\right)\in \mathcal{M}$，参数为 $w\in {\mathbb{R}}^d$，以及一个竞标者估价概要的样本 $S=\left\{v^{(1)},\dots ,v^{(L)}\right\}$，该样本为 $F$ 中独立同分布采样出。本文的目标是在满足激励相容的所有拍卖 $\mathcal{M}$ 中，找到一个能使负期望的收益 $-{\sum }_{i\in N}{p}_i^w(v)$ 最小化的拍卖。

在学习问题中需要引入一个约束以确保所选择的拍卖满足激励相容。在本文中，作者定义了 每位竞标者事后后悔的程度，以衡量拍卖违反激励相容的程度。固定其他竞标者的出价，考虑该竞标者所有可能的出价，则该竞标者的 事后后悔 是其效用的最大增加值。竞标者 $i$ 的期望事后后悔为
$${\mathrm{rgt}}_i(w)=\mathbf{E}\left[\underset{v_i^{\prime }\in V_i}{\max }{u}_i^w\left(v_i;\left(v_i^{\prime },v_{-i}\right)\right)-u_i^w\left(v_i;\left(v_i,v_{-i}\right)\right)\right]$$
其中，期望是在 $v\sim F$上的，并且给定模型参数 $\omega$ ，$u_i^w\left(v_i,b\right)=v_i\left(g_i^w(b)\right)-p_i^w(b)$。作者假设 $F$ 在估值概要 $V$ 的空间上有充分支持，并且认识到遗憾是非负的，当且仅当 $rg{t}_i(w)=0，\forall i\in N$ 时，拍卖满足 DSIC。

鉴于此，本文将学习问题重新表述为最小化期望损失（即每个竞标者产生的期望负收益），并有约束（期望事后后悔为0）：
$$\underset{w\in {\mathbb{R}}^d}{\min }{\mathbf{E}}_{v\sim F}\left[-\sum _{i\in N}{p}_i^w(v)\right]\text{ s.t. }rg{t}_i(w)=0,\forall i\in N.$$
给定来自 $F$ 的 $L$ 个估值概要的样本 $S$，本文估计竞标者 $i$ 的 经验事后后悔 如下：
$$\begin{array}{rl}& {\widehat{\mathrm{rgt}}}_i(w)=\frac{1}{L}\sum _{\ell =1}^L\underset{v_i^{\prime }\in V_i}{\max }{u}_i^w\left(v_i^{(\ell )};\left(v_i^{\prime },v_{-i}^{(\ell )}\right)\right)-u_i^w\left(v_i^{(\ell )};v^{(\ell )}\right)\end{array}$$
并寻求最大限度地减少经验损失，同时满足所有竞标者的经验事后后悔为零（式2）：
$$\begin{array}{cc}{\min }_{w\in {\mathbb{R}}^d}& -\frac{1}{L}{\sum }_{\ell =1}^L{\sum }_{i=1}^n{p}_i^w\left(v^{(\ell )}\right)\\ \text{ s.t. }& {\widehat{rgt}}_i(w)=0,\forall i\in N\end{array}$$

个体理性（Individual Rationality） 本文将额外要求设计的拍卖需要满足个体理性，这可以通过将本文的搜索空间限制到一类参数化拍卖 $(g^{\omega },p^{\omega })$ 来实现，此类拍卖对竞标者收取的费用不超过其分配的期望效用。

泛化边界

因为不是精确计算的，因此需要知道这个近似的误差有多大。泛化边界能够刻画这个误差的大小。

本文按照抽样的估值概要的数量，限制了期望后悔和经验后悔之间的差距，对收入也是如此。本文的边界适用于从有限容量类中选择的任何拍卖，并显示用大样本求解式 2 会得到一个期望收益接近最优且期望遗憾接近于零的拍卖（但在实践中，作者发现可能无法精确求解式 2）。

本文定义拍卖 $(g,p),\left(g^{\prime },p^{\prime }\right)\in \mathcal{M}$ 之间的 ${\ell }_{\infty ,1}$ 距离为 ${\max }_{v\in V}{\sum }_{i,j}\left|g_{ij}(v)-g_{ij}^{\prime }(v)\right|+{\sum }_i\left|p_i(v)-p_i^{\prime }(v)\right|$。对于任意 $\epsilon >0$，${\mathcal{N}}_{\infty }(\mathcal{M},ϵ)$ 表示在 ${\ell }_{\infty ,1}$ 距离下覆盖 $\mathcal{M}$ 的半径为 $ϵ$ 的最小球数。

2.2 神经网络结构

本文构建了一个神经网络称为 遗憾网络（RegretNet），用于建模多物品拍卖。本文考虑加性、单位需求和一般组合估值的三种竞标者。该体系结构包含两个逻辑上截然不同的组件：分配网络 和 支付网络。

加性估值（Additive valuations）

当竞标者对一捆物品 $S\in M$ 的价值估计为 $S$ 中每个物品的单价之和时（即 $v_i(S)={\sum }_{j\in S}{v}_i(j)$），则称竞标者是加性估值的。在这种情况下，竞标者只报告他们对单个物品的估价。随机分配网络 $g^w:{\mathbb{R}}^{nm}\to [0,1{]}^{nm}$ 和 支付网络 $p^w:{\mathbb{R}}^{nm}\to {\mathbb{R}}_{\ge 0}^n$，都被建模为具有 tanh 激活函数的前馈全连接网络。

网络的输入 由投标 $b_{ij}$ 组成，代表竞标者 $i$ 对物品 $j$ 的估值。

分配网络的输出 为对每个物品 $j\in [m]$，分配概率向量 $z_{1j}=g_{1j}(b),\dots ,z_{nj}=g_{nj}(b)$。为了确保可行性，即一个物品被分配的概率不超过1，分配概率使用 softmax 激活函数来计算，因此对于所有物品 $j$，${\sum }_{i=1}^n{z}_{ij}\le 1$。为了确保一件物品没有分配给任何投标人的可能性，作者在 softmax 计算中包含一个虚拟节点，该节点持有剩余分配概率。捆绑的物品是可能的，因为输出单元分配物品到同一竞标者可以是相关的。

支付网络的输出 为每个竞标者需要支付的付款，表示竞标者应针对该特定的投标概要预期支付的金额。

为了确保拍卖满足 个人理性，即不会向竞标者收取超过其预期分配价值的费用，网络首先使用 sigmoidal 单元为每个竞标者 $i$ 计算一个支付分数 ${\tilde{p}}_i\in [0,1]$，并输出支付 $p_i={\tilde{p}}_i{\sum }_{j=1}^m{z}_{ij}{b}_{ij}$，其中 $z_{ij}$ 为分配网络的输出。网络架构如下图所示，其中 收入和遗憾是由分配网络和支付网络的参数组成的函数计算的。

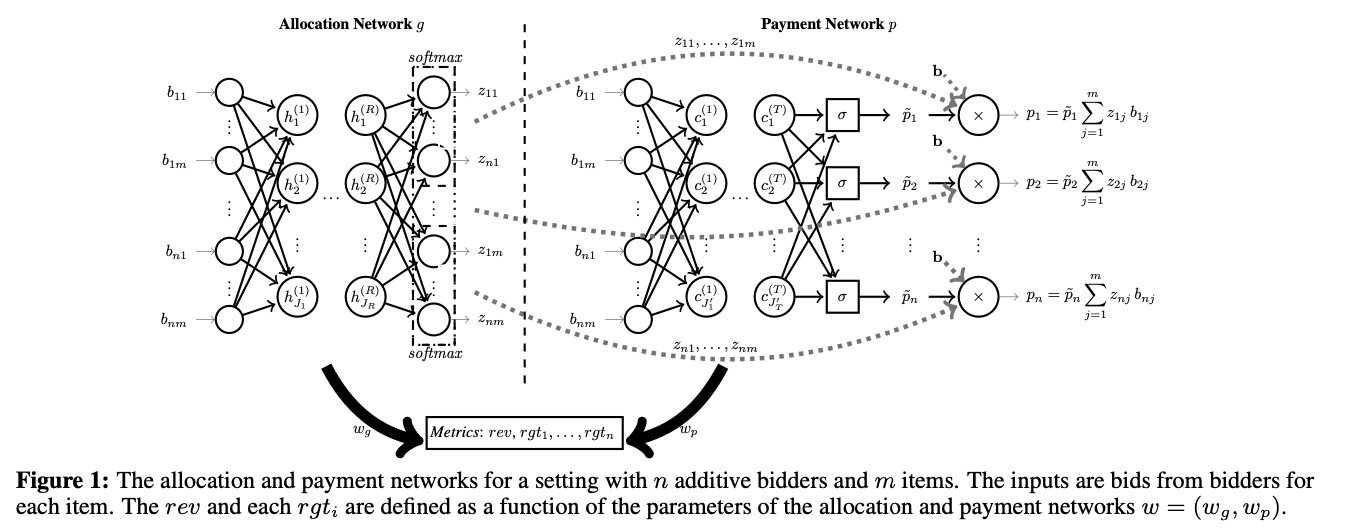
上图展示了 $n$ 个加性竞标者和 $m$ 个物品的拍卖。输入是每个竞标者对每个物品的出价（投标），将 $rev$ 和每个 $rg{t}_i$ 定义为 由分配网络和支付网络的参数组成的函数 $w=(w_g,w_p)$。

单位需求估值（Unit-demand valuations）

当竞标者对一捆物品 $S\in M$ 的价值估计为 $S$ 中物品的最高价格时（即 $v_i(S)={\max }_{j\in S}{v}_i(j)$），则称竞标者是单位需求估值的。分配网络 的结构如下图的（a）：

对于此设置中的收入最大化，可以证明 考虑将最多一个物品分配给每个投标人的分配规则就足够了。因此，对于随机分配规则而言，每个竞标者的总分配不超过 1，即 ${\sum }_j{z}_{ij}\le 1,\forall i\in [n]$，同时需要保证一个物品不会被过度分配，${\sum }_i{z}_{ij}\le 1,\forall j\in [m]$。因此，作者设计了一个输出概率 ${\left[z_{ij}\right]}_{i,j=1}^n$ 的矩阵是双随机的分配网络。分配网络计算两组分数 $s_{ij}$ 和 $s_{ij}^{\prime }$，第一组分数按行归一化，第二组分数按列归一化。这两个归一化都可以通过 softmax 函数来实现。然后，将竞标者 $i$ 和物品 $j$ 的分配作为相应归一化得分的最小值计算:

$$z_{ij}={\phi }_{ij}^{DS}\left(s,s^{\prime }\right)=\min \left\{\frac{e^{s_{ij}}}{{\sum }_{k=1}^{n+1}{e}^{s_{kj}}},\frac{e^{s_{ij}^{\prime }}}{{\sum }_{k=1}^{m+1}{e}^{s_{jk}^{\prime }}}\right\}$$
其中指数 $n+1$ 和 $m+1$ 表示虚拟输入，分别对应一个没有分配给任何竞标者的物品，和一个没有分配到任何物品的竞标者。

Lemma 1.

${\phi }^{DS}\left(s,s^{\prime }\right)$ 为双随机 $\forall s,s^{\prime }\in {\mathbb{R}}^{nm}$，对于任何双随机分配 $z\in [0,1{]}^{nm},\exists s,s^{\prime }\in {\mathbb{R}}^{nm}$，其中 $z={\phi }^{DS}\left(s,s^{\prime }\right)$ 。

支付网络 与 Figure 1 的相同。

组合估值（Combinatorial valuations）

本文也考虑了一般的组合估值。在目前的工作中，作者只针对少量的物品开发了该结构。在这种情况下，每个竞标者 $i$ 报告对每一捆物品 $S\subseteq M$ 的投标 $b_{i,S}$ （除了空的捆绑，此时估价为零）。分配网络 对每个竞标者 $i$ 和一捆物品 $S$ 有输出 $z_{i,S}\in [0,1]$，表示竞标者被分配到该捆物品的概率。为了防止物品被过度分配，作者要求一个物品出现在分配给某个投标人的捆绑包中的概率最多为 1。作者还要求分配给投标人的总金额不超过 1：
$$\begin{array}{c}\sum _{i\in N}\sum _{S\subseteq M:j\in S}{z}_{i,S}\le 1,\forall j\in M\\ \sum _{S\subseteq M}{z}_{i,S}\le 1,\forall i\in N\end{array}$$
为了保证组合的可行性，需要满足上面两式。为了实现这些约束，分配网络 给每个物品计算一组分数，同时给每个竞标者计算一组分数。即 对每个竞标者 $i\in N$ 有一组 bidder-wise 分数 $s_{i,S},\forall S\subseteq M$，和 对每个物品 $j\in M$ 有一组 item-wise 分数 $s_{i,S}^{(j)},\forall i\in N,S\subseteq M$。每一组分数都是用 softmax 函数进行归一化 ${\bar{s}}_{i,S}=\exp \left(s_{i,S}\right)/{\sum }_{S^{\prime }}\exp \left(s_{i,S^{\prime }}\right)$，${\bar{s}}_{i,S}^{(j)}=\exp \left(s_{i,S}^{(j)}\right)/{\sum }_{i^{\prime },S^{\prime }}\exp \left(s_{i^{\prime },S^{\prime }}^{(j)}\right)$。

竞标者 $i$ 和捆绑物 $S$ 的分配定义为 $i$ 的标准化 bidder-wise 分数和每个 $j\in S$ 的标准化 item-wise 分数的最小值，即：
$$z_{i,S}={\phi }_{i,S}^{CF}\left(s,s^{(1)},\dots ,s^{(m)}\right)=\min \left\{{\bar{s}}_{i,S},{\bar{s}}_{i,S}^{(j)}:j\in S\right\}$$

Lemma 2.

${\phi }^{CF}\left(s,s^{(1)},\dots ,s^{(m)}\right)$ 对 $\forall s,s^{(1)},\dots ,s^{(m)}\in {\mathbb{R}}^{n{2}^m}$ 为可行组合。对任何可行组合分配 $z\in [0,1{]}^{n{2}^m},\exists s,s^{(1)},\dots ,s^{(m)}\in {\mathbb{R}}^{n{2}^m}$，其中 $z={\phi }^{CF}\left(s,s^{(1)},\dots ,s^{(m)}\right)$。

Figure 2 的（b）展示了 2 个竞标者和 2 个物品设置的网络结构。为了便于解释，作者在讨论中忽略了空包。

对每个竞标者 i ∈ { 1 , 2 } i \in \{1,2\} i∈{1,2}，网络计算三个分数 s i , { 1 } , s i , { 2 } , s i , { 1 , 2 } s_{i,\{1\}}, s_{i,\{2\}}, s_{i,\{1,2\}} si,{1}​,si,{2}​,si,{1,2}​ ，其中一个是 $i$ 得到的分配情况，并使用 softmax 函数进行标准化。同时，网络对物品 1 也计算了四个分数 s 1 , { 1 } 1 , s 2 , { 1 } 1 , s 1 , { 1 , 2 } 1 , and  s 2 , { 1 , 2 } 1 s_{1,\{1\}}^{1}, s_{2,\{1\}}^{1}, s_{1,\{1,2\}}^{1} \text {, and } s_{2,\{1,2\}}^{1} s1,{1}1​,s2,{1}1​,s1,{1,2}1​, and s2,{1,2}1​，同样对物品 2 也计算四个分数 s 1 , { 2 } 2 , s 2 , { 2 } 2 , s 1 , { 1 , 2 } 2 ,  and  s 2 , { 1 , 2 } 2 s_{1,\{2\}}^{2}, s_{2,\{2\}}^{2}, s_{1,\{1,2\}}^{2}, \text { and }s_{2,\{1,2\}}^{2} s1,{2}2​,s2,{2}2​,s1,{1,2}2​, and s2,{1,2}2​。同样每一组分数也是用 softmax 函数进行标准化。最后，竞标者 $i$ 的分配为 z i , { 1 } = min ⁡ { s ˉ i , { 1 } , s ˉ i , { 1 } 1 } , z i , { 2 } = min ⁡ { s ˉ i , { 2 } , s ˉ i , { 2 } 2 }  and  z i , { 1 , 2 } = min ⁡ { s ˉ i , { 1 , 2 } , s ˉ i , { 1 , 2 } 1 , s ˉ i , { 1 , 2 } 2 } z_{i,\{1\}}=\min \left\{\bar{s}_{i,\{1\}}, \bar{s}_{i,\{1\}}^{1}\right\}, \quad z_{i,\{2\}}=\min \left\{\bar{s}_{i,\{2\}}, \bar{s}_{i,\{2\}}^{2}\right\} \text { and } z_{i,\{1,2\}}=\min \left\{\bar{s}_{i,\{1,2\}}, \bar{s}_{i,\{1,2\}}^{1}, \bar{s}_{i,\{1,2\}}^{2}\right\} zi,{1}​=min{sˉi,{1}​,sˉi,{1}1​},zi,{2}​=min{sˉi,{2}​,sˉi,{2}2​} and zi,{1,2}​=min{sˉi,{1,2}​,sˉi,{1,2}1​,sˉi,{1,2}2​}。

组合竞标者的支付网络与 Figure 1 的支付网络具有相同的结构，使用 sigmoidal 单元为每个竞标者 $i$ 计算支付分数 $\tilde{p}i\in [0,1]$，并输出支付 $p_i={\tilde{p}}_i{\sum }_{S\subseteq M}{z}_{i,S}{b}_{ij}$，其中 $z_{i,S}$ 是分配网络的输出。

泛化边界

2.3 优化与训练

本文使用 增广拉格朗日方法 在神经网络参数 $w$ 上求解式 2 的约束问题。首先定义了优化问题的拉格朗日函数，对违反约束的问题增广为二次惩罚项：
$$\begin{array}{rl}& {\mathcal{C}}_{\rho }(w;\lambda )=-\frac{1}{L}\sum _{\ell =1}^L\sum _{i\in N}{p}_i^w\left(v^{(\ell )}\right)+\sum _{i\in N}{\lambda }_i{\widehat{\mathrm{rgt}}}_i(w)+\frac{\rho }{2}{\left(\sum _{i\in N}{\widehat{\mathrm{rgt}}}_i(w)\right)}^2\end{array}$$
$\lambda \in {\mathbb{R}}^n$ 是拉格朗日乘子的向量，$\rho >0$ 是一个固定的参数来控制二次惩罚项的权重。求解器在模型参数和拉格朗日乘数的每次迭代中交替进行以下更新：

(a) $w^{\text{new }}\in {\mathrm{argmin}}_w{\mathcal{C}}_{\rho }\left(w^{\text{old }};{\lambda }^{\text{old }}\right)$

(b) ${\lambda }_i^{new}={\lambda }_i^{\text{old }}+\rho {\widehat{rgt}}_i\left(w^{new}\right),\forall i\in N$

作者将训练样本 $S$ 分成大小为 $B$ 的小批量，并对训练样本进行几次传递（每次传递后对数据进行随机变换）。本文将迭代 $t$ 时收到的小批量表示为 ${\mathcal{S}}_t=\left\{u^{(1)},\dots ,u^{(B)}\right\}$。对 (a) 的更新是 ${\mathcal{C}}_{\rho }$ 对参数 $w$ 的无约束优化，是用基于梯度的方法进行优化。

让 $rg{t}_i(w)$ 表示 (1) 中在小批量 $S_t$ 上计算的经验遗憾。 固定 ${\lambda }_t$ 的 ${\mathcal{C}}_{\rho }$ 的参数，即 $w$，由下式给出：
$$\begin{array}{rl}& {\nabla }_w{\mathcal{C}}_{\rho }\left(w;{\lambda }^t\right)=-\frac{1}{B}\sum _{\ell =1}^B\sum _{i\in N}{\nabla }_w{p}_i^w\left(v^{(\ell )}\right)+\sum _{i\in N}\sum _{\ell =1}^B{\lambda }_i^t{g}_{\ell ,i}+\rho \sum _{i\in N}\sum _{\ell =1}^B\widetilde{{\mathrm{rgt}}_i}(w)g_{\ell ,i}\end{array}$$
其中，
$$g_{\ell ,i}={\nabla }_w\left[\underset{v_i^{\prime }\in V_i}{\max }{u}_i^w\left(v_i^{(\ell )};\left(v_i^{\prime },v_{-i}^{(\ell )}\right)\right)-u_i^w\left(v_i^{(\ell )};v^{(\ell )}\right)\right]$$
需要注意的是，$\widetilde{{\mathrm{rgt}}_i}$ 和 $g_{l,i}$ 包含了投标人 $i$ 和估值概要 $l$ 的“最大” 误报，也就是这两项都需要去求别的估值带来最大的效用。本文使用另一个基于梯度的优化器来解决误报的内部最大化，并通过最佳误报处的效用之差计算梯度。本文对每个投标人 $i$ 和估值概要 $l$ 维护了一个估值误报 $v_i^{\prime (\ell )}$。对于模型参数 $w_t$ 的每次更新，执行 $R$ 次梯度更新以计算最佳误报：
$${v_i^{\prime }}^{(\ell )}={v_i^{\prime }}^{(\ell )}+\gamma {\nabla }_{v_i^{\prime }}{u}_i^w\left(v_i^{(\ell )};\left(v_i^{(\ell )},v_{-i}^{(\ell )}\right)\right)$$
本文使用 Adam 优化器 来更新模型 $w$ 和 ${v_i^{\prime }}^{(\ell )}$。

由于所求解的优化问题是非凸的，因此 求解器不能保证得到全局最优解。然而，实验证明本文的方法是非常有效的。学习到的拍卖具有较低的遗憾值，同时在某些已知最优拍卖的设置中，他与最优拍卖的结构密切匹配。

3 有什么关键的实验结果？

本文通过实验证明证明，该方法可以对已知最优解的几乎所有设置恢复接近最优拍卖，并且可以为没有已知解析解的设置找到新的拍卖。

3.1 实验设置

本文基于 Tensorflow 深度学习算法库实现算法代码，对所有的网络和隐藏节点的 tanh 激活函数使用了 Glorot uniform 初始化。对于所有的实验，作者使用 640000 个估值概要 的样本进行训练，使用 10000 个估值概要 的样本进行测试。增广拉格朗日求解器运行了最多 80 个epoch，小批量大小为 128。在增广拉格朗日量中 $\rho$ 值设为 1.0，每 2 个 epoch 增大一次。使用 Adam 优化器对每个小批量进行 $w_t$ 更新，学习率为 0.001。对于 $w_t$ 上的每一次更新，运行 R = 25 个误报更新步骤，学习率为 0.1。在 25 次更新结束时，缓存当前小批的优化错误报告，并用于在下一个时期初始化同一小批的错误报告。每 100 个小批量（即 Q = 100）对 ${\lambda }_t$ 进行一次更新。本文的实验是在一个具有 NVDIA GPU 核心的计算集群上运行的。

3.2 实验评估

除了在测试集中学习拍卖的 收入，本文还对 遗憾 进行评估，平均在所有投标人和测试估值概要，$ret=\frac{1}{n}{\sum }_{i=1}^n{\widehat{rgt}}_i(f,p)$。作者通过在 2000次 迭代中对步长为 0.1 的 $v_i^{\prime }$ 运行梯度上升来评估这些项（我们测试了1000个不同的随机初始 $v_i^{\prime }$，并报告获得最大遗憾的那一个）。

3.3 单竞标者

即使在单竞标者拍卖的简单设置中，也只有在特殊情况下才有分析解。本文给出了 第一种能够处理一般设计问题的计算方法，并与现有的分析结果进行了比较。实验表明，该方法不仅能够学习接近最优收益的拍卖，而且还能够学习与理论上最优规则相似的分配规则，其准确性令人惊讶。

1. 单竞标者，2 个物品，加性估值。物品的价值为 $U[0,1]$ 中采样而来。

   该设置的最优拍卖方案：

   Manelli, A. and Vincent, D. Bundling as an optimal selling mechanism for a multiple-good monopolist. Journal of Economic Theory, 127(1):1–35, 2006.

2. 单竞标者，2 个物品，单位需求估值。 物品的价值为 $U[2,3]$ 中采样而来。

   该设置的最优拍卖方案：

   Pavlov, G. Optimal mechanism for selling two goods. B.E. Journal of Theoretical Economics, 11:1–35, 2011.

下图展示了测试集上设置 1 和 2 的最终拍卖的收益和遗憾，该测试集的架构有两个隐藏层，每层100个节点。

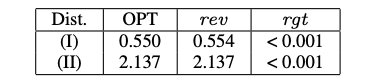
学习的拍卖的收益非常接近于最优收益，遗憾很小。在某些情况下，学习的拍卖的收益略高于最优激励相容拍卖的收益。下图中学习的 分配规则 的可视化显示，本文的方法近似地地恢复了最优拍卖的结构。

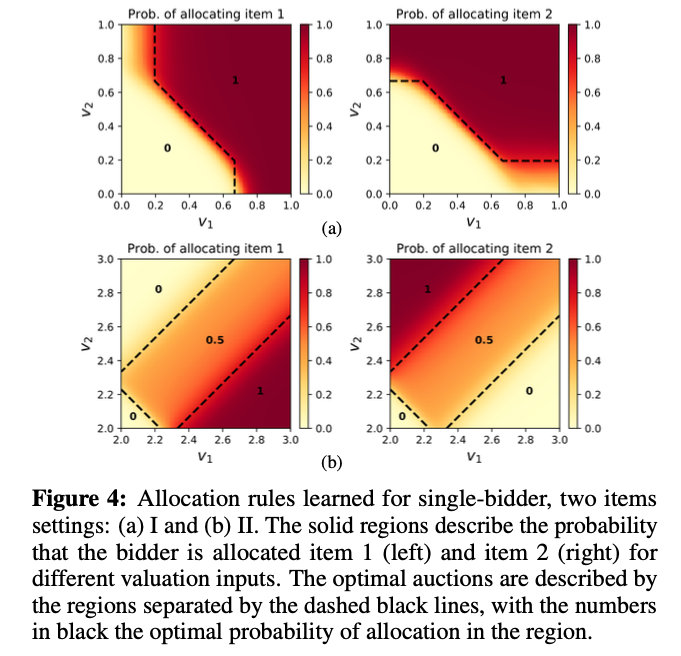
最优拍卖用黑色虚线分隔的区域来描述，黑色的数字表示该区域的最优分配概率。

下图展示了收入和遗憾关于时间函数的曲线。

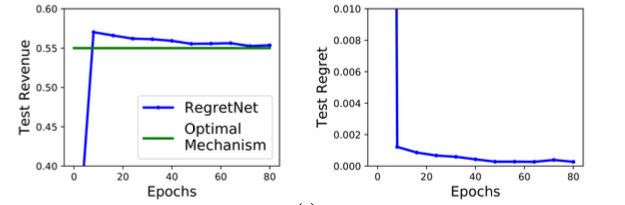
3.4 多竞标者

接下来，作者将本文方法与 state-of-the-art 方法的结果进行比较，在这些实验环境中，最优拍卖机制是未知的。这些拍卖是通过搜索一个参数化的激励相容拍卖类得到的。不像这些先前的方法，本文不需要搜索一个特定的激励兼容拍卖类，并且只受限于使用的网络的表达能力。实验证明，本文设计的新的拍卖设计，匹配或超过最先进的机制。

Sandholm, T. and Likhodedov, A. Automated design of revenue-maximizing combinatorial auctions. Operations Research, 63(5):1000–1025, 2015.

3. 2 个竞标者，加性估值，2 个物品，物品的价值从 $U[0,1]$ 中采出。
4. 2 个竞标者，2 个物品。$v_{1,1}, v_{1,2}, v_{2,1}, v_{2,2} \sim U[1,2],\ v_{1,{1,2}}=v_{1,1}+v_{1,2}+C_{1} $ 并且 v 2 , { 1 , 2 } = v 2 , 1 + v 2 , 2 + C 2 v_{2,\{1,2\}}=v_{2,1}+v_{2,2}+C_{2} v2,{1,2}​=v2,1​+v2,2​+C2​，其中 $C_1,C_2\sim U[-1,1]$。
   1. 2 个竞标者，2 个物品。 v 1 , 1 , v 1 , 2 ∼ U [ 1 , 2 ] v 2 , 1 ,   v 2 , 2 ∼ U [ 1 , 5 ] ,   v 1 , { 1 , 2 } = v 1 , 1 + v 1 , 2 + C 1 v_{1,1}, v_{1,2} \sim U[1,2] v_{2,1}, \ v_{2,2} \sim U[1,5],\ v_{1,\{1,2\}}=v_{1,1}+v_{1,2}+C_{1} v1,1​,v1,2​∼U[1,2]v2,1​, v2,2​∼U[1,5], v1,{1,2}​=v1,1​+v1,2​+C1​ 并且 v 2 , { 1 , 2 } = v 2 , 1 + v 2 , 2 + C 2 v_{2,\{1,2\}}=v_{2,1}+v_{2,2}+C_{2} v2,{1,2}​=v2,1​+v2,2​+C2​，其中 $C_1,C_2\sim U[-1,1]$。

本文采用与设置 1、2 相同的实验设置。并将训练后的机制与来自 (Sandholm & Likhodedov, 2015) 的 $VVCA$ 和 $AM{A}_{bsym}$ 激励兼容拍卖系列的最佳拍卖进行比较。

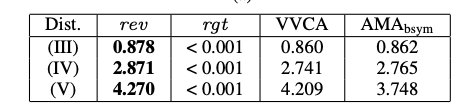
本文的方法带来了显著的收益改善和微小的遗憾。

3.5 扩大拍卖规模

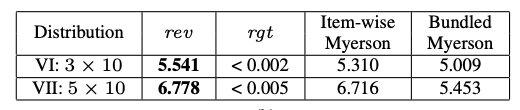
作者进一步扩大规模至 5 个竞标者和 10 个物品的拍卖。由于问题的指数性质，这比现有分析文献可以处理的要复杂几个数量级。对于本文所研究的设置，在投标人数量的限制下，对每件物品进行单独的 Myerson 拍卖是最优的（Palfrey, 1983）。这产生了一个非常强大但仍可改进的基准。

5. 3 个竞标者，加性估值，10 个物品，估值从 $U[0,1]$ 中采样。
6. 5 个竞标者，加性估值，10 个物品，估值从 $U[0,1]$ 中采样。

对于设置 5，作者在下图中显示了通过不同架构获得的 10000 个概要的验证样本上的收益和遗憾。图中 $(R,K)$ 代表着网络有 $R$ 层，每层 $K$ 个节点。对于上述两种设置，在所有 100 个节点的网络中，(5,100) 架构的遗憾程度最低。

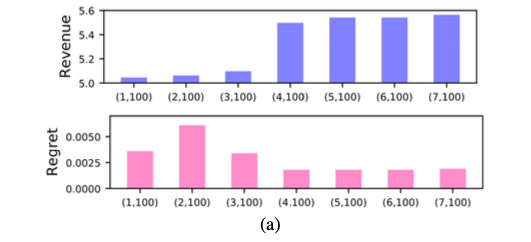
与基线相比，最终学习的拍卖产生了更高的收益（有微小的遗憾）。

3.6 与线性程序相比

作者将算法的运行时间与 LP 方法进行了比较（Conitzer & Sandholm, 2002;2004）。为了能够运行 LP 来完成，本文考虑一个更小的设置，包括 2 个竞标者，加性估值，和 3 个物品，物品价值来自 $U[0,1]$。利用 commercial solver Gurobi 对该问题进行求解。本文通过将每个物品的值离散化到 5 个箱子（得到 $\approx 10^5$ 个决策变量和 $\approx 4\times 10^6$ 个约束）来处理连续的估值，然后将连续输入的估值概要舍入到最近的离散概要（用于评估）。由于粗略的离散化，LP 方法遭受严重的 IR 违规（并因此产生更高的收入）。

对于更精细的离散化，我们无法在超过1周的计算时间内运行此设置的 LP。相比之下，我们的方法产生更低的遗憾和没有违反 individually rational （因为神经网络满足 IR 设计），在大约9个小时。事实上，即使对于更大的设置(VI) - (VII)，我们算法的运行时间也不到13小时。