入门强化学习（Q-learning→DQN→DDQN）

基础：

• 只要具备CNN分类算法的基本认识。

讲解内容：

1. 内容主要通过《飞翔小鸟》游戏为例，探究如下2个问题：
   • 强化学习原理：以Q-learning算法为例。
   • 深度强化学习原理：以DQN、DDQN算法为例。
2. 然后大概讲下DDQN算法，如何在更复杂的解锁任务中应用和设计。

学完收获：

• 认真看完所有细节内容，基本就能了解一种强化学习和一种深度强化学习的整个过程，其他算法可以举一反三。

备注：由于资料大多从PPT中截取出来，转成文章可能会有一些不理解的地方，如有细节疑问可以留言提出来。

0 应用背景

《飞翔小鸟》是一款简单的手机游戏：

• 操作：唯一的操作是手指点击屏幕。
• 操作效果：每点击一下，画面中小鸟就挥动一下翅膀往上突然蹬飞一下（非匀速运动！），如果不点击屏幕，小鸟就会做自由落体运动。小鸟不能前后移动，只能上下飞翔或自由落体，背景画面会匀速从左网友移动。
• 游戏得分：你唯一要做的就是让小鸟不撞上那些绿色的管道，每通过一个管道口，分数+1。
• 游戏操作难点：小鸟蹬飞速度是非匀速的，先快后慢。然后下降速度也是非匀速的自由落地。图中通道口每次出现位置随机，如果前后两个通道口高度差较大，那么就要在短时间内让小鸟快速爬升，并恰当好的下降回去。

1 强化学习原理

强化学习定义：

        强化学习（Reinforcement Learning, RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题。

强化学习要素：

        强化学习中有状态（state）、动作（action）、奖赏（reward）这三个要素。

强化学习如何发挥作用：

        智能体（Agent）会根据当前状态来采取动作，并记录被反馈的奖赏，以便下次再到相同状态时能采取更优的动作。

Q-Learning算法怎么自己玩《飞翔小鸟》

利用Q-Learning强化学习算法，我们可以让智能体程序去玩《小鸟飞翔》游戏。

Q-Learning是强化学习算法中value-based的算法，Q即为Q-table（一个价值表）就是在某一时刻的 s 状态下，采取动作 a 能够获得收益的期望，环境会根据agent的动作反馈相应的奖励 r，所以算法的主要思想就是将 State 与 Action 构建成一张 Q-table 来存储Q值，然后根据Q值来选取能够获得最大的收益的动作。

针对《小鸟飞翔》游戏，我们对强化学习三要素建模如下：

• 状态的选择：取小鸟到下一组管子的水平距离和垂直距离差作为小鸟的状态。
• 动作的选择：每一帧，小鸟只有两种动作可选：1.向上飞一下。2.什么都不做。
• 奖赏的选择：小鸟活着时，每一帧给予1的奖赏；若死亡，则给予-1000的奖赏。

探究1：Q-Learning强化学习是要训练什么东西？

本质上，

 探究2：Q-Learning强化学习如何训练？

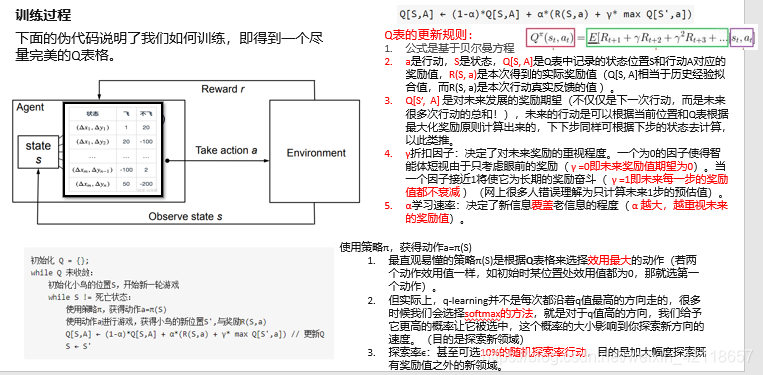
 2 深度强化学习原理

Q-learning算法有个最大问题：高维等场景下，创建出来的Q-table会过于庞大，甚至无法穷尽。（因为很多场景下，状态无法穷尽、动作无法穷尽、所以它们两者形成的Q-table价值表也就无法穷尽）

2012年，当AlexNet深度学习刚在ImageNet比赛大获全胜时，2013年，DeepMind团队就想到把深度网络与强化学习结合起来（主要就是用CNN网络替换Q-table），巧妙地解决了状态维数爆炸的问题！

2015年《Nature》封面刊登了DeepMind 改进版DQN深度强化学习算法。

具体细节请详细看懂下面PPT，不然后面看不懂了：

 DQN算法结构和奖励函数

DQN算法架构和奖励函数如下：

具体细节如下：

 Q-leaning和DQN训练流程对比

 DQN算法如何进一步优化：Double-DQN算法

 3 DDQN解决OpenLock任务

OpenLock任务源自《人类因果迁移:深度强化学习的挑战》。

3.1 OpenLock规则介绍

1. Agent 只有 3 个动作：推下杠杆、拉回杠杆、推门。

2. Agent 每次 都只有 3 次动作机会， 3 次动作后，门没解锁，则场景恢复初始状态。

开门的四种方法：

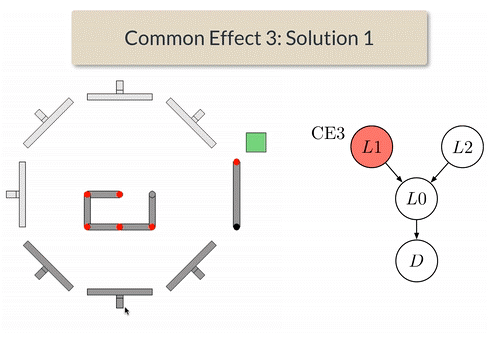
• L：代表场景中一个深色杠杆。编号就是ID。
• D：开门
• CC3 意思就是我推了L0杆子，那么再推L1或L2任意一个后，门就显示可以去打开了。
• CE3 意思是我需要推了L1或L2之后，再去推L0，门才显示可以去打开。

3.2 DDQN如何设计来解决此任务？

DDQN的设计方法如下：