机器人工作空间解析分析
机器人空间是指机器人末端执行器运动描述参考点所能达到的空间点的集合。在规划机器人任务时,往往需要首先知道机器人的可达空间。所以我们可以用蒙特卡洛随机采样的方法,对各个关节角在关节范围内进行随机选取,取大量的采样点进行计算,通过正运动学求解, 即可得到相应的末端位置,同构绘制大量末端位置点即可可视化机器人工作空间。
 图1 PRR三维工作空间 图1 PRR三维工作空间
|
 图2 PRR工作空间(俯视) 图2 PRR工作空间(俯视)
|
1、工作空间如何量化
以PRR构型机器人为例,可采用柱坐标来描述。
柱坐标描述:(r,φ,z) r∈[357.096,1042.90] φ∈[-pi,pi] z∈[790.119,1090.119]
 图3 仿真工作空间(正视) 图3 仿真工作空间(正视)
|
 图4 仿真工作空间(俯视) 图4 仿真工作空间(俯视)
|
2、判断空间位置是否在工作空间内
将笛卡尔坐标系转换至柱坐标系,判断是否在范围之内
r
=
x
2
+
y
2
r= \sqrt {x^{2}+y^{2}}\,
r=x2+y2
ϕ
=
a
r
c
t
a
n
(
y
x
)
\phi=arctan(\frac{y}{x})
ϕ=arctan(xy)
z
=
z
z=z
z=z
3、常见曲面描述
a.常见曲面解析式
球面:
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
+
(
z
−
z
0
)
2
=
R
2
(x-x_0)^{2}+(y-y_0)^{2}+(z-z_0)^{2}=R^{2}\,
(x−x0)2+(y−y0)2+(z−z0)2=R2
柱面:
x
2
+
y
2
=
R
2
x^{2}+y^{2}=R^{2}\,
x2+y2=R2
抛物柱面:
y
2
=
2
x
y^{2}=2x\,
y2=2x
 图5 球面图 图5 球面图
|
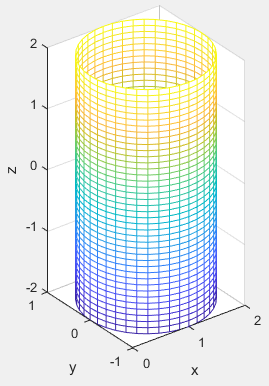 图6 柱面图 图6 柱面图
|
 图7 抛物面图 图7 抛物面图
|
旋转曲面: f ( y , z ) = 0 f(y,z)=0 f(y,z)=0,绕z轴旋转后, f ( ± x 2 + y 2 , z ) = 0 f(±\sqrt {x^{2}+y^{2}}\,,z)=0 f(±x2+y2,z)=0
 图8 待旋转曲线 图8 待旋转曲线
|
 图9 旋转曲面图 图9 旋转曲面图
|
b.参考论文《机械手工作空间边界曲面的解析表达式》

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








