03、滤波器设计——阶跃阻抗低通滤波器

1、设计指标

用微带或带状线实现低通滤波器的一种相对容易的方法是用很高和很低特征阻抗的传输线交替排列的结构。这种滤波器通常称为阶跃阻抗(Stepped-Impedance)或高Z一低Z滤波器，由于它结构紧凑且较容易设计，所以比较流行。然而，它的电特性不是很好，故通常应用于不需要有陡峭截止响应的场合。

（1）具有最平坦响应（巴特沃斯）。
（2）截止频率为2.5GHz（通带截止频率）。
（3）在4GHz处的插入损耗必须大于20dB（阻带截止频率及其波纹）。
（4）所设计滤波器的阻抗为50Ω，具有最平坦响应，采用6阶巴特沃兹低通原型，最高实际线阻抗为120Ω,最低实际线阻抗为20Ω，采用的基片参数，铜导体的厚度t=0.035mm。

2、低通滤波器设计步骤

（1）根据设计要求确定低通原型的元器件值（阶数）。

（2）集总元件→高低阻抗线→微带线

电感↔高阻线↔线细（太细则功率太小）

电容↔低阻线↔线宽（不可与波长比拟）

2.1、低通原型滤波器设计

先计算：

 由图可知，对于n=6的曲线，当为0.6时，LA>20dB,故最大平坦滤波器计数n=6。

 由表给出的低通原型值：g1=0.517，g2=1.414，g3=1.932，g4=1.932，g5=1.414，g6=0.517，g7=1（50Ω电阻）。

 2.2、滤波器原理图设计

由低通原型电路转换到微带电路主要就是得到理想传输线的电长度，再利用Start TineCalc转换到微带线。

低通原型→理想传输线电长度（弧度制）

电感：

电容：

其中为滤波器阻抗=50Ω。

一般高阻选择100左右，低阻选择20左右。

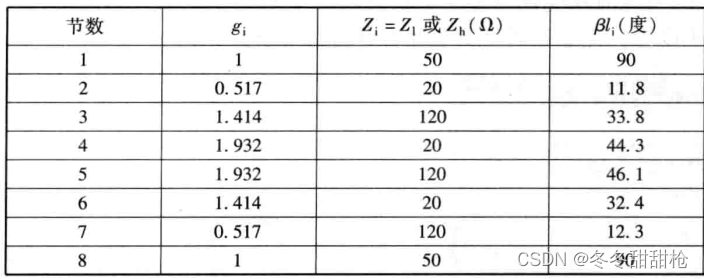
再利用Start TineCalc工具转换到微带线

最终原理图（为了方便后续优化，微带线宽度长度用变量代替）

注：微带线宽度只受阻抗的影响，微带线长度受阻抗和电长度两个因素影响。

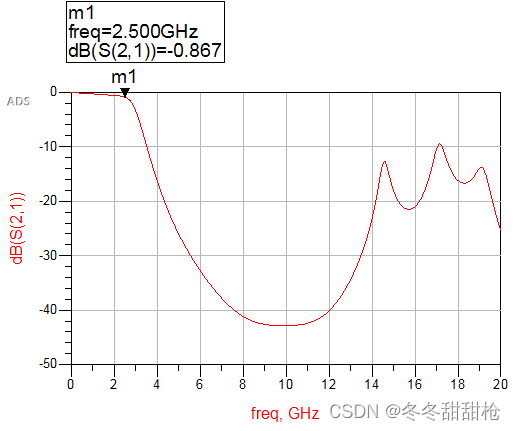
 2.3、仿真结果

 可以看到仿真结果未达到设计要求，需要进一步优化。

3、滤波器电路参数优化

仿真优化原理图：

注意GOAL的设置，dB(S(1,1)),SP1,以及频率后面的单位Ghz都要输入正确。

至于优化可先用Random（随机） 大范围搜索，再用Gradient（梯度）局部收敛，优化后进一步修改优化变量范围多次优化。

 优化后的仿真结果：

 可见优化后依旧未满足设计指标，则需要进一步优化和改进。

4、其他参数仿真

（1）寄生通带

滤波器在其他频率成分上会产生寄生通带。

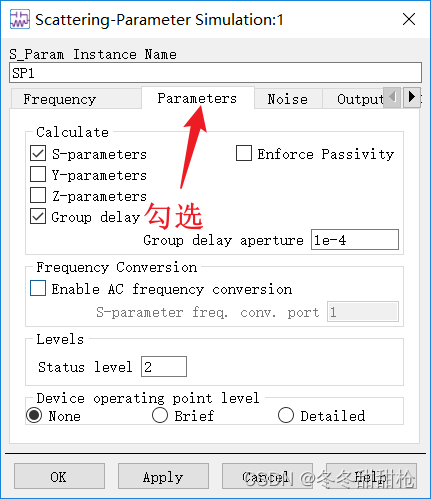
 （2）群延时

指信号通过滤波器所需要的时间。

 注意修改纵坐标的大小

5、微带滤波器版图生成与仿真

（1）版图的生成

使两个Term、接地、集总元器件、以及仿真控件失效。

 Layout→Generate/Update Layout生成板图，并加上端口

 （2）EM电磁仿真设置

填入微带线板层结构：

H= 25mil(基板的厚度)

Er=9.9(基板的相对介电常数)

Mur=1(基板的磁导率常数)

Cond=4.1E+7(微带线走线层所使用的金属导体(表面导体)的导电率)

Hu默认(空气腔与PCB板层的距离，上层空气的厚度)

T=0.7mil(金属(表面导体)厚度)

TanD=0.0009(基板损耗角正切)

（3）仿真结果

 可见版图仿真和原理图仿真有很大差别，需要重新回到原理图窗口进行优化仿真。