

必读 → 收藏!2020年智慧汽车供应链俱乐部&智慧企培学院 课程计划
2019年10月乘用车综合销量排名快报,一汽大众遥遥领先
2019年10月在售485款车销量排行(全)轿车/SUV/MPV,10月新能源遭遇腰斩
2020 俱乐部课程超级优惠年卡,限量发售
热门课程 |确定开课,GD&T 公开课苏州18期,12.21-12.22

点击图片即可查看详情(苏州第十八期确定开课,准时开课,ASME认证高级GD&T专家吴老师授课,中国产品几何技术规范标准化委员;(授课依据最新(ASME14.5-2018和ISO1101-2017)的内容授课)
非对称轮廓度与动态轮廓度
在机械工程图中,对于异形曲面,我们只能采用轮廓度(线轮廓度和面轮廓度)进行控制。除了采用常规的轮廓度(即对称轮廓度)控制,还可以采用其他轮廓度,如非对称轮廓度,动态轮廓度,复合轮廓度等等。
今天我们主要聊非对称轮廓度和动态轮廓度。
本期文章我们要讨论的话题有以下几个:
1.ISO/ASME中修饰符号(U圈和UZ)前后的数字表示什么意思?
2. U圈前后的数字可以为负号吗?前后数字的大小有范围要求吗?
3. U圈和动态轮廓度之间是否有关系?
1. 非对称轮廓度
不管是ISO还是ASME,轮廓度默认都是对称分布的。所谓对称分布,指的的是公差带的两个边界相对于理论轮廓是对称分布的(严格意义上讲,不是对称,是两侧的偏置量相同而已),如下图所示:

a图纸标注

b公差带分布
图1 图纸标注和公差带分布
图1中的宽度为0.5的公差带,是将理论轮廓内外各偏置(Offset)公差带的一半(0.25)形成的,只要被测零件的实际表面能够落在这个宽度为0.5的公差带范围内,该实际被测表面就是合格的。
联想到尺寸要素的尺寸公差,轮廓度其实和下图概念的逻辑是一致的。

图2 尺寸公差
根据GB/T 1800,图2中Φ20表达的是公称尺寸(即零线),js表达该轴的公差的基本偏差属于对称分布,而7则表示精度等级为IT7,对于公称尺寸为Φ20的尺寸而言,它决定了其公差的大小是0.02(需要查表)。
轮廓度属于几何公差,为什么我们要扯这个尺寸公差呢?因为通过尺寸公差的3大要素(1. 公称尺寸, 2. 基本偏差, 3公差)就可以确定尺寸要素的具体尺寸公差,这个最基本的底层逻辑同样适用于几何公差。
尤其是非对称公差,研究这种最基本的底层逻辑更有意义。
先来看一下非对称轮廓度。
本公众号的第一篇文章就介绍了非对称轮廓度,这里只做简单介绍。先看看美标,见图3:

a 图纸标注
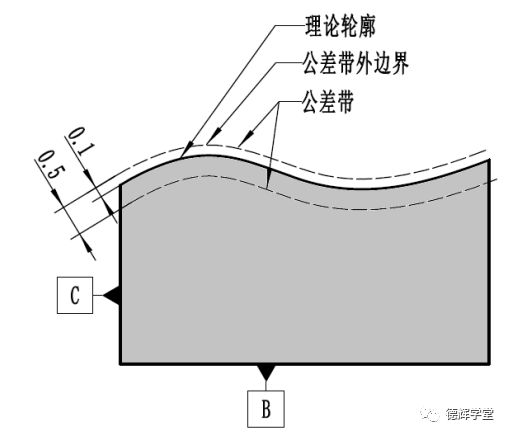
b 公差带分布
图3 非对称轮廓度与公差带
根据图3中的图纸标注,一旦采用U圈(美标),公差带相对于理论轮廓通常就是非对称分布的。那么它是怎么分布的呢?
根据美标Y14.5-2018或者Y14.5-2009中规定,U圈前面的数值表达的是公差值(0.5),U圈后边的数值表达的是公差带外边界相对于理论轮廓在加材料方向的偏置量(0.1),见图3中b图。
需要注意的是,加材料方向,实际上就是理论轮廓的法向(正方向是材料里指向材料外)。

图4 尺寸公差
我们再来扯扯尺寸公差,对比着来认识非对称轮廓度。如果采用公差代号来表达尺寸公差,我们发现除了基本偏差代号为JS和js以外的所有公差都是非对称分布的(建议参考GB/T1800.1或者ISO286-1)。
图4中轴的尺寸公差用公差代号Φ20g7表达,同样,表达尺寸公差的三大要素分别为:
Φ20表达的是公称尺寸,决定了0线的位置
g表达的是基本偏差(孔用大写字母,轴用小写字母),决定了公差相对于0线的偏差为0.007
7决定了公差值的大小为0.021
对比非对称轮廓度公差,同尺寸公差一样,表达它也同样需要三大要素:
理论轮廓(相当于尺寸公差中的公称尺寸Φ20)
偏置量,即U圈后面的数值,表示公差带外边界相对于理论轮廓的偏置量0.1(相当于尺寸公差中的g)
公差带大小,即U圈前面的数值,表示公差带总宽度为0.5(相当于尺寸公差中的7级精度等级)
具体见图5:
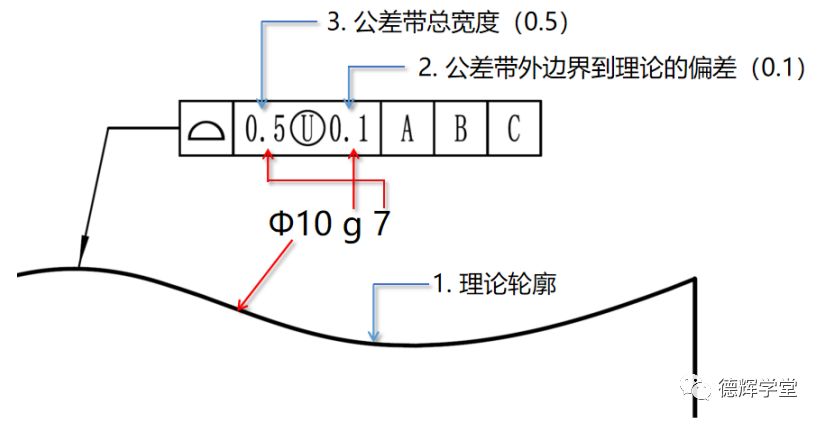
图5 几何公差与尺寸公差的共同逻辑
假如我们用尺寸公差的形式来表达图3中的非对称轮廓度,我们可以说它的要求是+0.1到-0.4(当然,这个仅用于口头交流)。
我们再来看看ISO中的非对称轮廓度是怎么回事。
基于同样的逻辑,认识ISO中的非对称轮廓度就很容易,ISO中非对称公差的修饰符号是UZ(注意,没有圈),见下图:

a 图纸标注
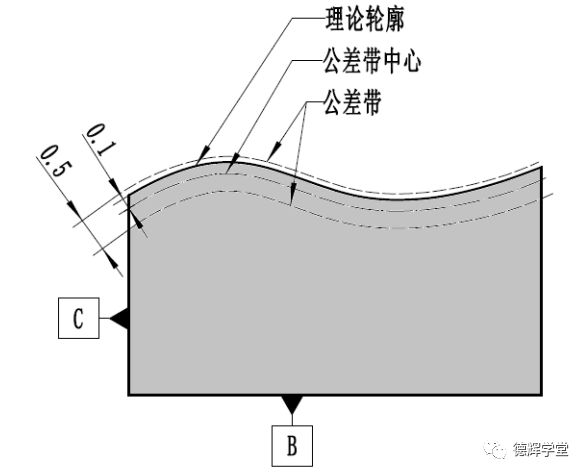
b 公差带分布
图6 ISO图纸标注和公差带分布
根据ISO的概念可知,修饰符号UZ前面的数值表达的是公差带的总宽度0.5,UZ后边的数值表达的是公差带的中心相对于理论轮廓的偏置量0.1(负号表达在公差带中心在材料里边,而正号则表达公差带中心在材料外边)。具体见图6。
我们仔细观察,也会发现ISO也是基于3大要素来表达非对称轮廓度公差的:
理论轮廓。
偏置量,即UZ后边的数值,表示公差带中心相对于理论轮廓的偏置量为0.1,负号表示方向,意思是公差带的中心在材料里边。
公差带大小,即UZ前面的数值,表示公差带总宽度为0.5。
对比ISO和ASME中的非对称轮廓度,UZ和U圈前面的数值都表示公差带的总宽度,这一点两个标准是相同的。唯一差别在于修饰符号U圈和UZ后边的数值,即偏置量的计算方式不一样,起点都是理论轮廓,但终点不一样。
1. ASME表达的是理论轮廓到公差带外边界的偏置量
2. ISO表达的是理论轮廓到公差带中心的偏置量
到这里,我们稍作总结,轮廓度公差的逻辑和尺寸公差的逻辑是一样的,无非就包含3个信息:1. 理论轮廓;2. 偏置量;3. 公差大小。ISO和ASME各自修饰符号(U圈和UZ)前面的数值都表达的是公差带的总宽度,U圈和UZ后边都表达的是偏置量,只是U圈的偏置量是从公差带外边界开始算,UZ的偏置量是从公差带中心开始算。
设计工程师为什么要采用非对称轮廓度呢?
如同尺寸公差要采用非对称公差一样,常见的应用工况之一就是为了“配合”。比如下图所示:
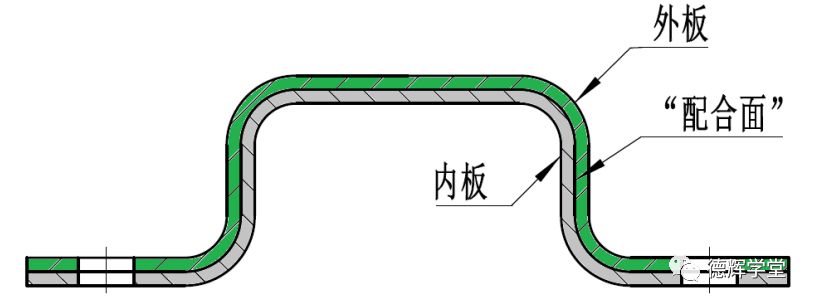
图7 内外板
图7中的外板和内板会焊接在一起,内板主要起到加强作用。内外板的“配合面”在数模上是零贴的,在焊接之前,我们希望外板的内槽大一些,内板则小一些。也就是说我能希望外板和内板之间的配合属于间隙配合。
这时,我们就可以采用非对称轮廓度控制,见图8和图9。
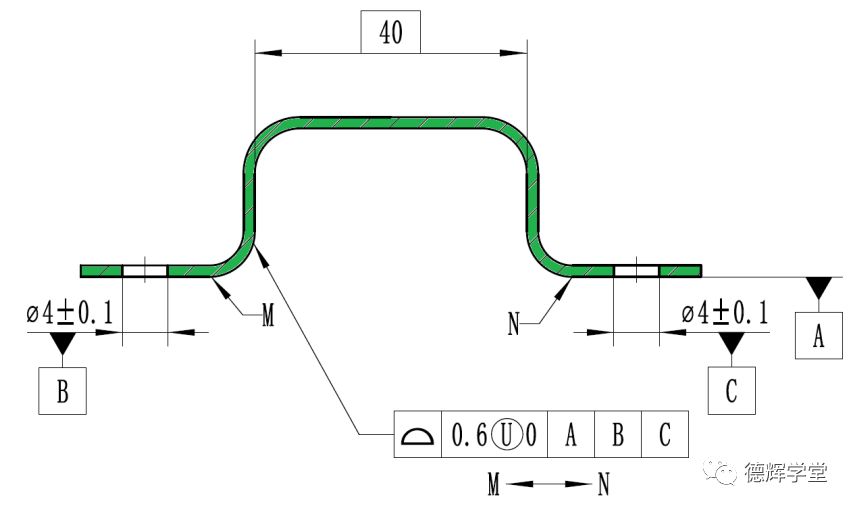
图8 外板图纸
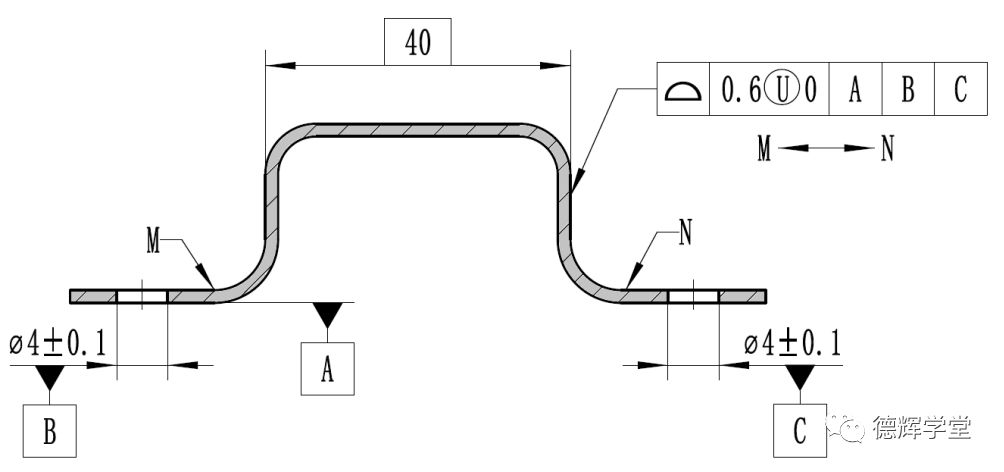
图9 内板图纸
图8中外板的配合面(内槽)采用非对称轮廓度控制,公差带相当于0到-0.6,这样会导致图8中内槽宽40的实际尺寸只会偏大,不会偏小。而图9中正好相反,它的公差带也是0到-0.6,会导致(外凸)宽度40的实际尺寸只会偏小,不会偏大。能够实现“间隙配合”。
具体偏大多少,偏小多少,我们把它设置成一道练习题,放在文章最后,供大家练习用。
2. U圈和UZ前后数值的范围
接下来,进入在业界经常争论的一个话题,U圈前边和后边的数值是否都可以为负?U圈后边数值大小是否一定要比U圈前边的数值小?
这个话题之所以会成为业界争论的一个话题,那是因为根据最权威的依据-ASME Y14.5-2018, 对该话题它没有给出明确的说法,所以行业内不同的老师可能有不同的看法。
但是&#








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2037
2037

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








