问卷调查分析-spss

小白15138

已于 2024-06-10 10:52:07 修改

阅读量2.7k

点赞数 19

分类专栏： spss 文章标签： python

于 2024-04-02 10:15:25 首次发布

本文链接：https://blog.csdn.net/weixin_42712867/article/details/137042943

版权

spss 专栏收录该内容

5 篇文章

订阅专栏

文章目录

一、数据预处理
二、描述性统计分析
- 2.1 人口学变量频率分析
三、信效度检验
三、显著性检验
3.1 结果变量在性别上的显著性检验
3.2 结果变量在年龄上的显著性检验
3.3 结果变量在报告人上的显著性检验
3.4 结果变量在地区上的显著性检验
三、相关分析

一、数据预处理

1.1 数据预处理

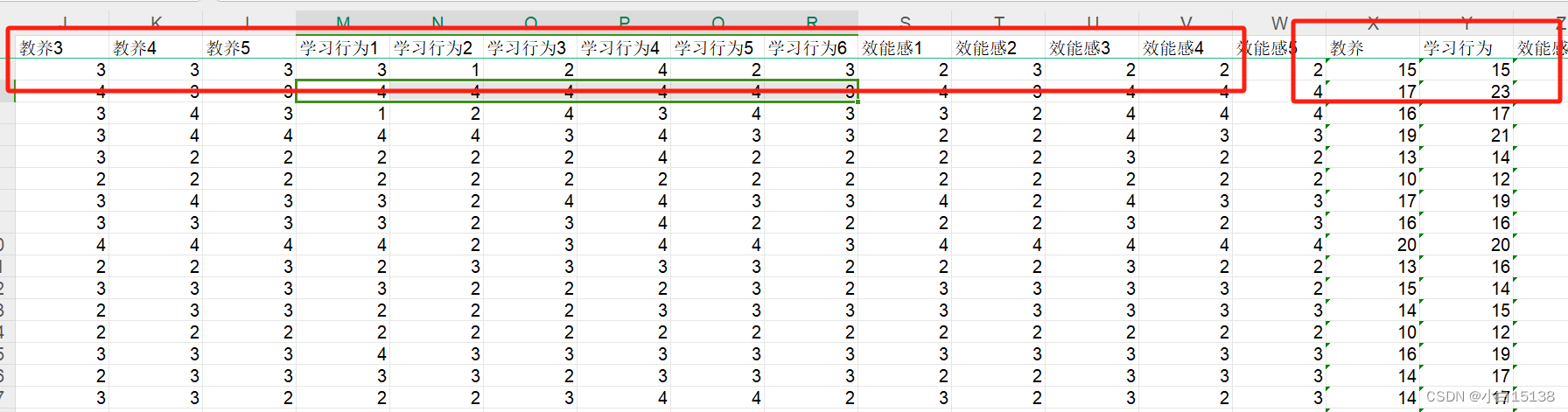
在拿到数据的时候需要对数据进行预处理比如缺失值、异常值、重复数据等进行处理，一般问卷调查都是针对某个方向进行多个问题的提问以保证结果的准确性，例如本次分析的问卷调查就对学习行为进行了5个问题提问，所以需要对这5个问题的回答的得分进行求和。同理也需要处理教养、和效能感。如图所示：
在这里插入图片描述

1.2 数据导入

如果是Excel数据，在spss-文件-导入数据-Excel中进行数据导入，找到Exce文件点击打开，选择对应的工作表，导入表格数据。如图所示：
在这里插入图片描述

1.3 数据定义

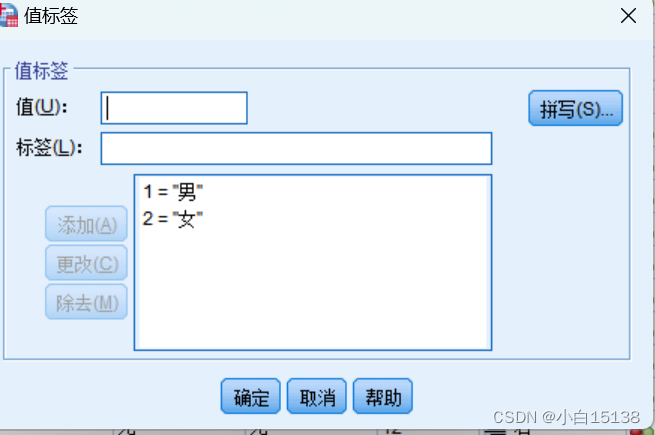
在我们的问卷调查中，一般会有被调研人员的基本信息（一般有10个左右的题），而这些数据一般都是用数值进行表示，这时就需要我们来对这些数值代表的含义进行配置，例如性别这一列用1代表男2代表女，这样的列需要我们对值进行定义。在spss的变量视图（可在此视图中配置各列的属性）中“值”这一列进行配置，如图所示，值填写列中值，标签填写此值代表的含义，然后点击添加按钮就完成此值的配置。
在这里插入图片描述

二、描述性统计分析

2.1 人口学变量频率分析

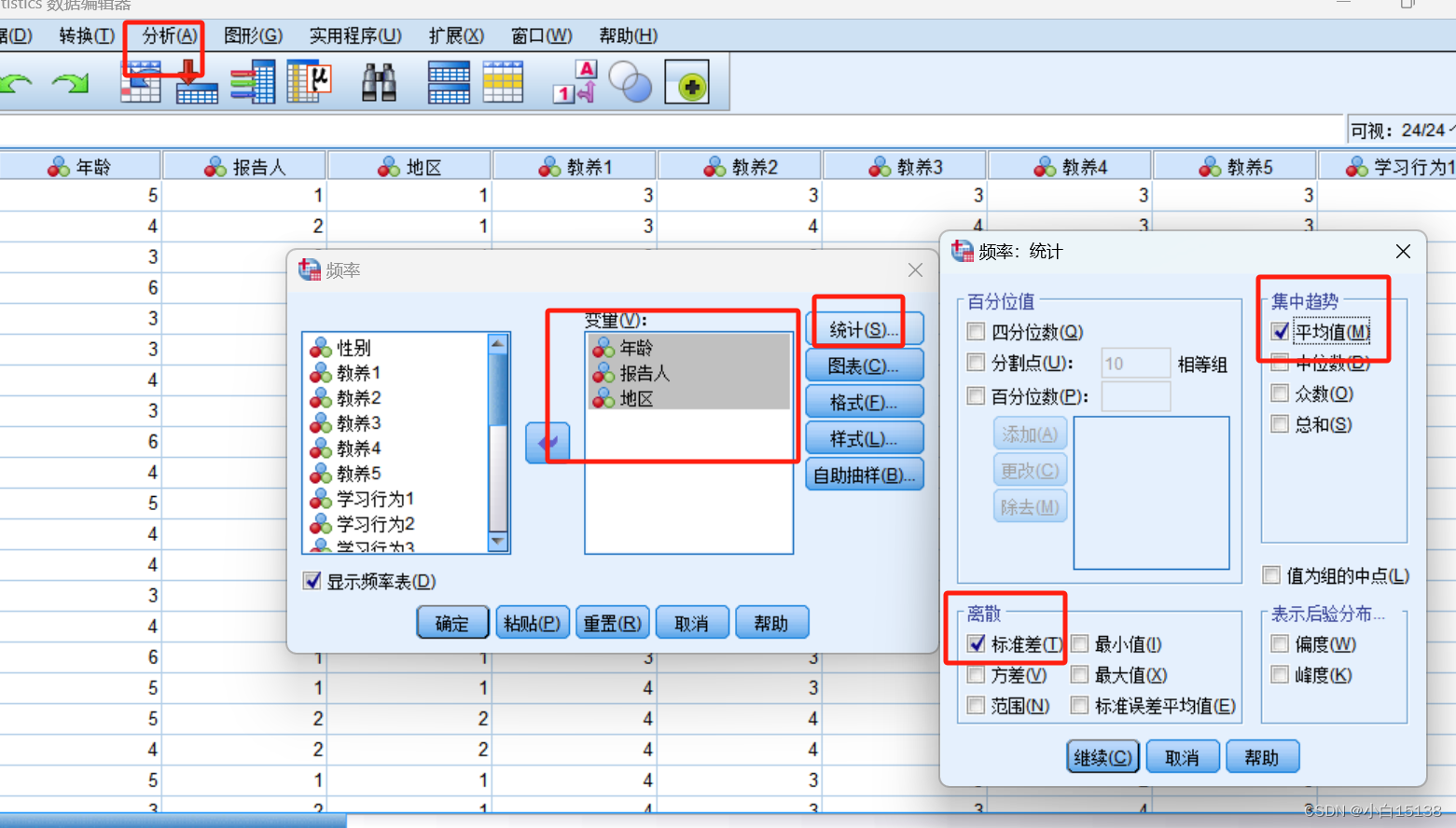
对被调研者基本信息进行人口学变量频率分析，选择spss-分析-描述统计-频率，然后选择要进行分析的人口学变量，选择统计，在选择分析指标，如图所示。
在这里插入图片描述

然后对结果进行整理成我们需要的样式，去除不必要展示的指标。结果如下：

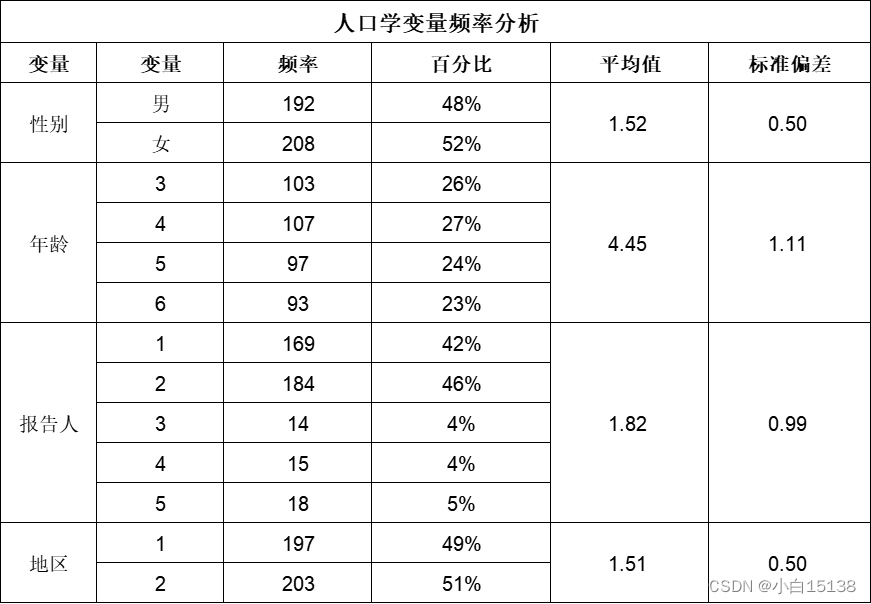
根据以上的分析结果可以看出人口学变量的数值特征，反映了本次被调查对象的分布情况。其中均值代表了集中趋势，标准差代表了波动情况。
根据各个变量的频率分析结果，可以看出分布基本满足抽样调查的要求。如，其中男性占比48%，女性占比52%，男女比例基本一致。

三、信效度检验

3.1 信度检验

信度即可靠性，它是指采用同样的方法对同一对象重复测量时所得结果的一致性程度。信度指标多以相关系数表示，大致可分为三类：稳定系数（跨时间的一致性），等值系数（跨形式的一致性）和内在一致性系数（跨项目的一致性）。信度分析的方法主要有以下四种：重测信度法、复本信度法、折半信度法、信度系数法。
通常认为，信度系数应该在 0～1 之间，如果 Cronbach α系数在 0.9 以上，表示信度很好；如果系数在 0.8～0.9 之间，表示信度可以接受；如果量表的信度系数在 0.7～0.8 之间，表示有些项目需要修订；如果量信度系数在 0.6 以下或者总量表的信度系数在 0.80 以下，应考虑重新修订量表或增删题项。

3.1.1 教养信度分析

对问卷调查中关于教养的五个变量进行信度分析，在spss-分析-标度-可靠性分析，选中关于教养的五个变量进行分析，模型选择默认的Alpha模型，点击统计按钮，然后选择需要统计的项（注意需要选中删除项后的标度，其他的可以不选），如图所示：
在这里插入图片描述
结果如图所示：

然后对结果进行整理成我们需要的样式，去除不必要展示的指标。结果如下：

根据以上的信度分析结果可以看出，在教养上总体的标准化信度系数为0.82，根据项删除后的信度系数可以看出都是小于总体的0.82，所以教养的题目满足信度检验不需要进行调整。
总体的标准化信度系数为0.82，信度系数在0-1之间，越接近1可靠性越高。本次分析的结果为0.82，相对来说信度较好。
注意：这里使用的是基于标准化项的Alpha其实也可以直接使用Alpha。

3.1.2 学习行为信度检验

对问卷调查中关于学习行为的六个变量进行信度分析，在spss-分析-标度-可靠性分析，选中关于学习行为的五个变量进行分析，模型选择默认的Alpha模型，点击统计按钮，然后选择需要统计的项（注意需要选中删除项后的标度）结果如图所示：
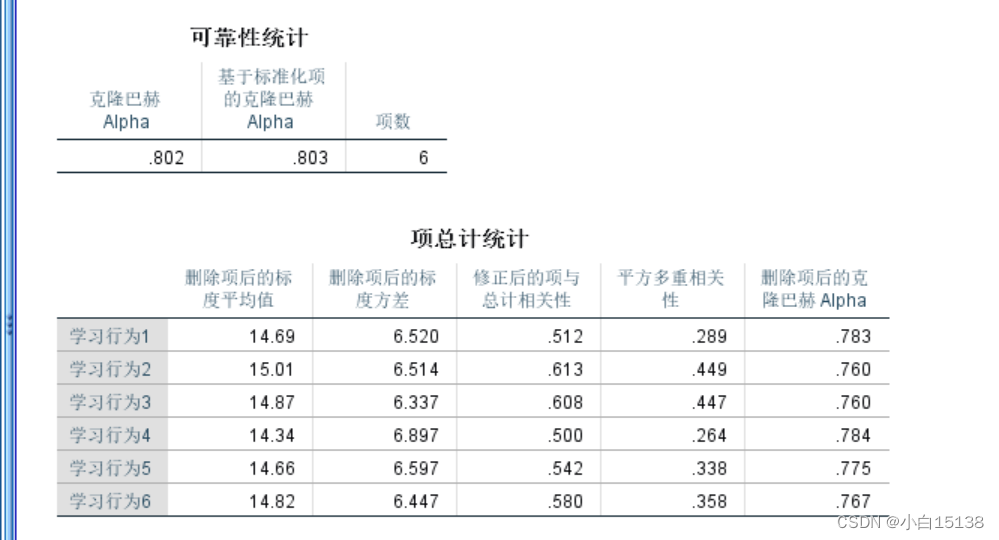
在这里插入图片描述

然后对结果进行整理成我们需要的样式，去除不必要展示的指标。结果如下：
在这里插入图片描述

根据以上的信度分析结果可以看出，在学习行为上总体的标准化信度系数为0.803，根据项删除后的信度系数可以看出都是小于总体的0.803，所以学习行为的题目满足信度检验不需要进行调整。
总体的标准化信度系数为0.803，信度系数在0-1之间，越接近1可靠性越高。本次分析的结果为0.803，相对来说信度较好。

3.1.3 效能感信度检验

对问卷调查中关于效能感的五个变量进行信度分析，在spss-分析-标度-可靠性分析，选中关于效能感的五个变量进行分析，模型选择默认的Alpha模型，点击统计按钮，然后选择需要统计的项（注意需要选中删除项后的标度）结果如图所示：
在这里插入图片描述

然后对结果进行整理成我们需要的样式，去除不必要展示的指标。结果如下：
在这里插入图片描述

根据以上的信度分析结果可以看出，在效能感上总体的标准化信度系数为0.839，根据项删除后的信度系数可以看出都是小于总体的0.839，所以效能感的题目满足信度检验不需要进行调整。
总体的标准化信度系数为0.839，信度系数在0-1之间，越接近1可靠性越高。本次分析的结果为0.839，相对来说信度较好。

3.1.4 总体信度检验

对问卷调查中所有的量表16个变量进行总体的信度分析，在spss-分析-标度-可靠性分析，选中关于总体的16个变量进行分析，模型选择默认的Alpha模型，点击统计按钮，然后选择需要统计的项（注意需要选中删除项后的标度）结果如图所示：
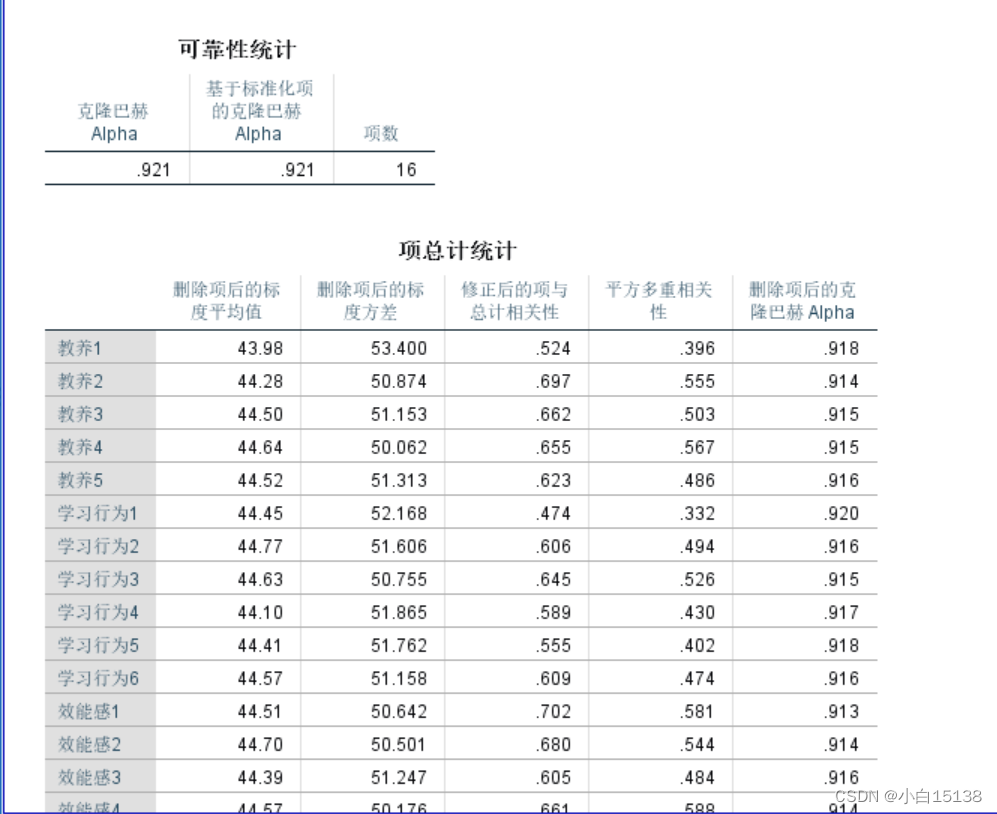
在这里插入图片描述

在这里插入图片描述

然后对结果进行整理成我们需要的样式，去除不必要展示的指标。结果如下：
在这里插入图片描述

总体的标准化信度系数为0.921，信度系数在0-1之间，越接近1可靠性越高。本次分析的结果为0.921，说明问卷总体的可信度非常高

3.2 效度检验

效度是指能够准确测出所需研究的事物的程度，即有效性。对前期所回收的400 份调查问卷通过spss探索性因子的方法实现检验过程。在-spss-分析-降维-因子分析，选中所有的量表列进行分析，点击描述按钮，选择初始解和KMO和巴特利特球形度检验。如图所示。
在这里插入图片描述
具体结果如下：

对结果进行整理并进行说明：

根据以上探索性因子分析的结果可以看出，KMO检验的系数为0.927，KMO检验的系数取值范围在0-1之间，一般认为 KMO 的值在0.7-0.8 之间适合做因子分析，大于 0.8 以上表明量表的效度较好。
根据球形检验的显著性也可以看出，本次检验显著性无限接近于0，拒绝原假设，所以问卷具有良好的效度。

三、显著性检验

显著性检验主要用来对我们结果变量在我们的分类变量上是否显著，结果变量是我们上面数据预处理中对多个学习行为变量求和得到的学习行为总分变量，对多个效能感变量求和得到的效能感总分变量，对多个教养变量求和得到的教养总分变量。
一般分类变量只有两个水平的时候进行独立样本T检验，多于两个水平用

3.1 结果变量在性别上的显著性检验

由于性别变量只有两个水平（男、女）所以使用独立样本T检验、操作步骤为spss-分析-比较平均值-独立样本T检验，如图所示：
参考文档独立样本T检验
在这里插入图片描述
选择教养、学习行为、效能感作为检验变量，选择性别作为分组变量，并点击分组变量的定义组按钮进行定义组。

最终结果如下：

当方差齐性结果的显著性 > 0.05，表明方差齐性，t检验结果中看第一行，当方差齐性结果的显著性 < 0.05，表明方差不齐性，t检验结果看第二行。例如教养这一显著性检验，方差齐性显著性检验为0.990大于0.05，t检验结果看第一行t为-0.484，sig为0.628

对结果进行整理并进行解释说明
在这里插入图片描述
根据以上独立样本T检验的结果，可以看出各个维度在性别上的差异情况。教养在性别上的差异显著性检验为0.63大于0.05，说明不同性别在教养上无显著差异。同理学习行为和效能感在性别上无显著性差异。
注意如果有显著性差异需要根据均值看谁大谁小

3.2 结果变量在年龄上的显著性检验

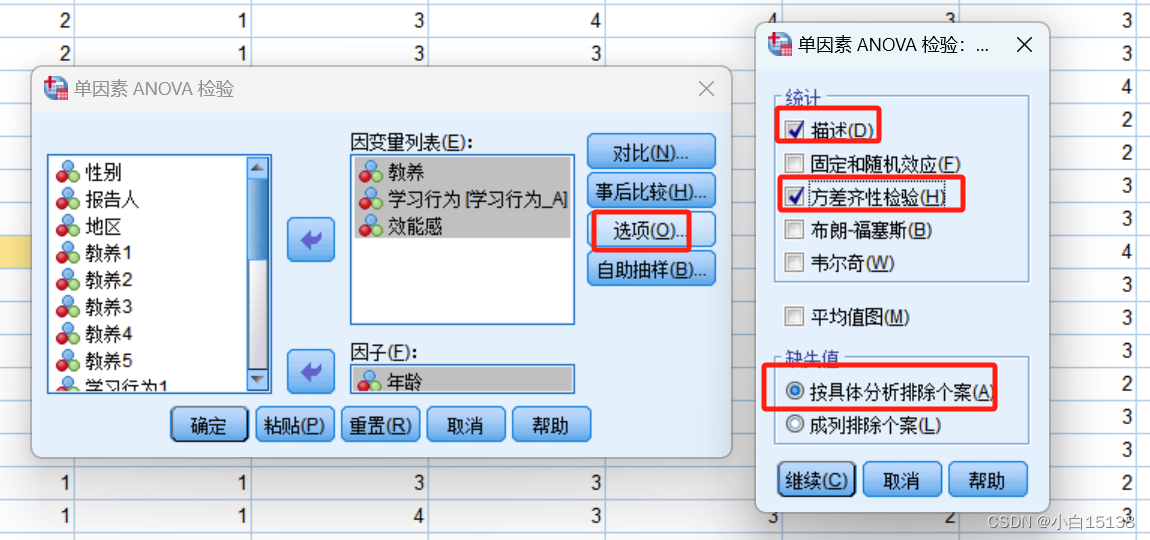
由于年龄变量有4个水平（3,4,5,6）大于2个水平，所以使用单因素方差分析、操作步骤为spss-分析-比较平均值-单因素方差分析，如图所示：
参考资料单因素方差分析
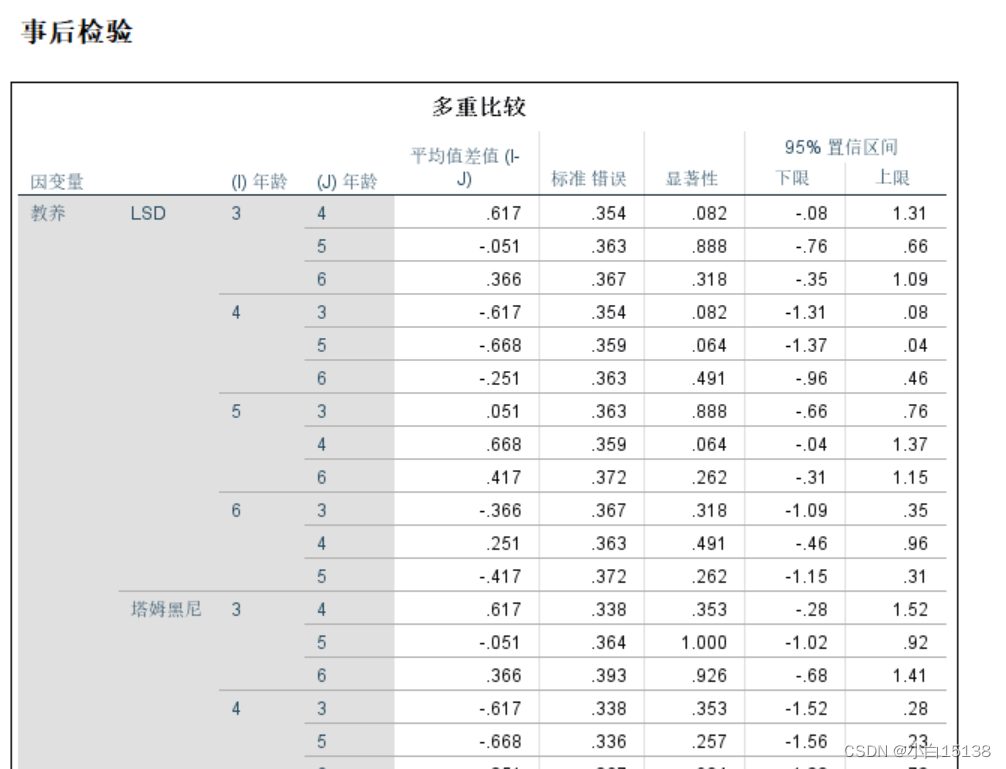
在这里插入图片描述
选择教养、学习行为、效能感作为检验变量，选择年龄作为分组变量，并点击事后比较按钮，勾选LSD及塔姆黑尼两个选项。

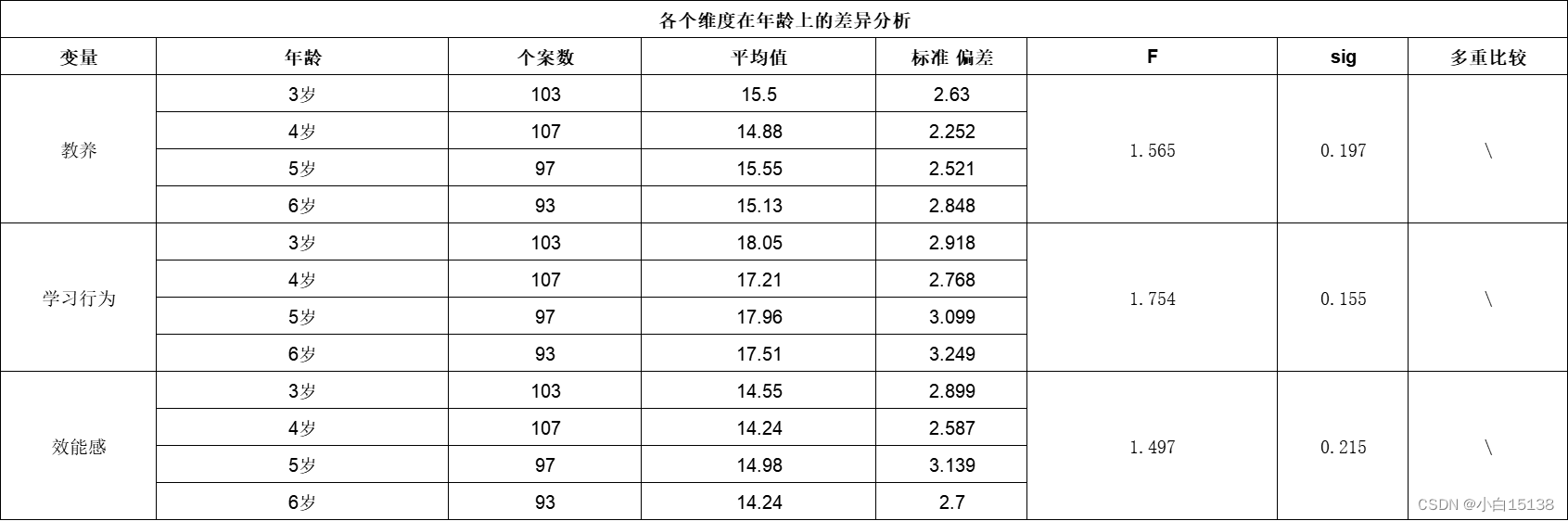
在这里插入图片描述
点击选项按钮，统计选择描述和方差齐性检验，缺失值选择按具体分析排除个案。

结果如下：

上表是描述性统计数据，一般只展示个案数、平均值和标准差就可以
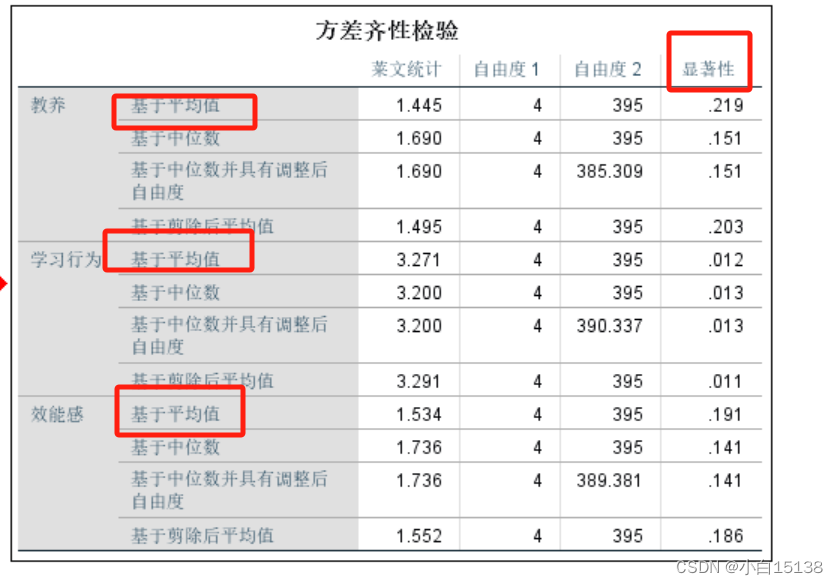
在这里插入图片描述
上表为方差齐性检验结果，主要关注最后一列基于平均值的显著性，当显著性 > 0.05，表明方差齐性，方差齐性则事后检验结果LSD检验结果即可，否则看塔姆黑尼检验结果。本表中显示所有的基于平均值的显著性均>0.05，表明方差齐性。
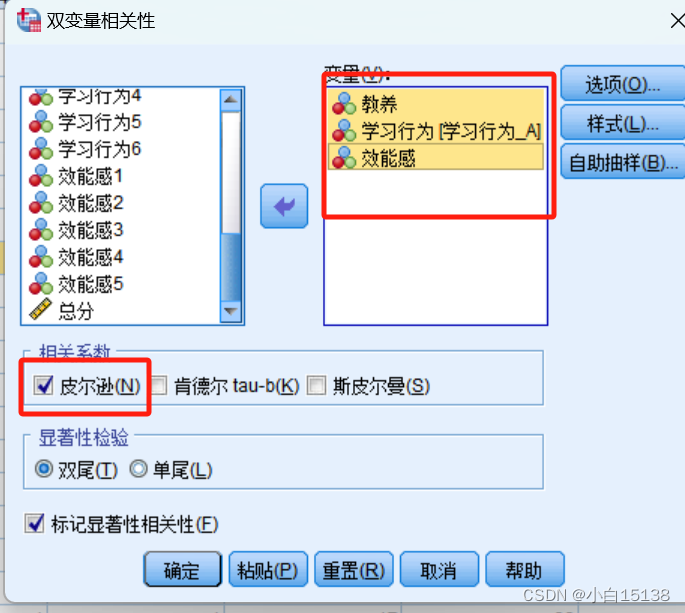
在这里插入图片描述
上表F检验结果，主要关注最后一列的显著性，当显著性< 0.05时，表明存在显著差异，本表中的显著性均>0.05，表明不存在显著差异，则下表的事后检验就不用看了。

上表为当F检验结果为显著时，用来看具体差异情况的，主要关注平均值差值以及显著性两列，且当上表的方差齐性检验结果显示为方差齐性时（显著性结果>0.05）结果看LSD部分，当方差齐性显示为方差不齐时（显著性结果<0.05）结果看塔姆黑尼部分。本分析中F检验结果均不显著所以不用看此表。