本节介绍PWM调制、SPWM调制的原理
本节介绍PWM功率放大器的结构、特性
概述
与线性功率放大器相比,开关功率放大器损耗小、效率高、输出功率大。缺点是会产生强烈的电磁干扰和噪音。
开关电路有两种基本模式:斩波控制和相位控制。
把直流变成矩形脉冲波的工作方式成为斩波。斩波常用的一种方法是固定开关的频率,并根据需要改变每个周期的占空比。按照这种方式工作的放大器称为脉冲宽度调制型放大器,也就是PWM功放
电机的控制方式一般是:

常用的可控直流电源有:
- 旋转变流机组(G-M系统)
即Genarator-Motor系统。用交流电动机带动直流发电机,获得可调的直流电压。目前已经基本不用 - 静止式(晶闸管)可控整流器(V-M系统)
即Varistor-Motor系统。用可控整流器获得可调的直流电压。目前主要用于大容量系统 - 直流斩波器/脉宽调制变换器(PWM变换器)
使用恒定或不控整流电源供电,利用电子电力开关器件斩波或进行脉宽调制,产生可变的平均电压
单管控制时称为直流斩波器。采用各种脉冲调制开关的电路称为脉宽调制变换器。
PWM变换器控制电机调速的优点:
1.主电路线路简单,需要的功率器件少
2.开关频率高,谐波少,电机损耗及发热小
3.低速性能好,稳速精度高,调速范围宽(可达1:10000)
4.与快速响应的电机配合,系统频带宽、动态响应快、动态抗扰能力强
5.开关器件导通损耗小,开关频率适当时,开关损耗也小,装置效率高
6.可以采用不控整流,电网功率因数比相控整流器高
以上提到的PWM变换器,实际就是PWM功放
PWM原理
脉宽调制,通过对一系列脉冲的宽度进行调制,来等效地获得所需要的波形(形状和幅值)
如利用直流斩波电路电路可以调制出不同幅值的直流波形
SPWM波可以等效正弦波形
能够进行PWM调制是由于面积等效原理,即冲量相等而形状不同的窄脉冲加在具有惯性的环节上,其效果基本相同。

正弦脉宽调制SPWM
使用一组等幅不等宽的矩形脉冲来等效正弦波。
脉冲幅值不变而宽度变化称为脉宽调制,当脉宽按正弦规律变化时则称为正弦脉宽调制,即SPWM
将正弦波等宽分段,按照每段的中心确定矩形脉冲的位置,使正弦波每个分段的面积等于对应矩形脉冲的面积,即矩形脉冲宽度按照正弦规律变化


对于负半周,则是脉冲的幅值取负
PWM功放输出级
采用H型桥式电路,由4个IGBT和4个续流二极管组成。AB为输出端,直流电动机为负载
IGBT输入PWM信号(控制极写作B,也可写作G),信号的频率和周期就是开关频率和开关周期
分析假设:
1.忽略晶体管开关过程和电源内阻
2.开关周期短,一个周期内电机转速及反电势为常值
3.电枢回路用电阻、电感、反电势等效

4.电磁转矩平均值和负载转矩平衡时,放大器-电机处于准稳定状态,电枢电流周期性变化
双极性输出
所有IGBT都输入PWM信号,14相同,23相同,14与23相反

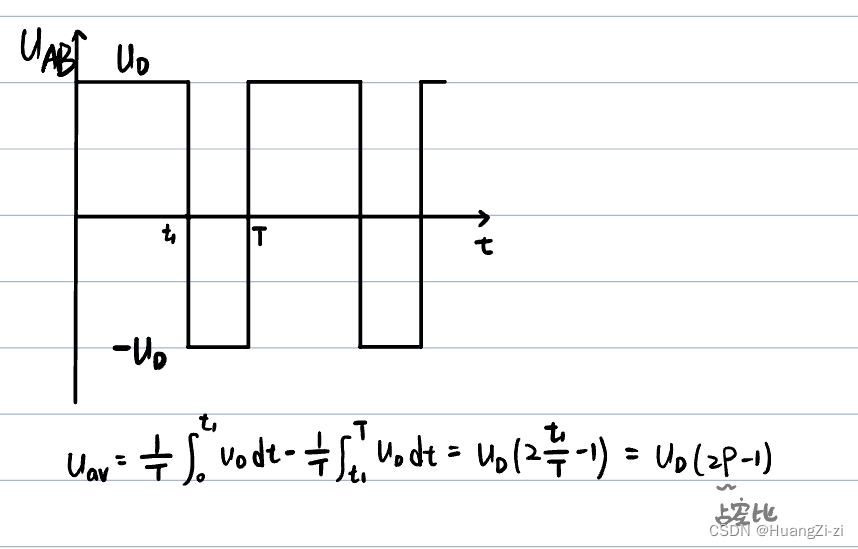
-
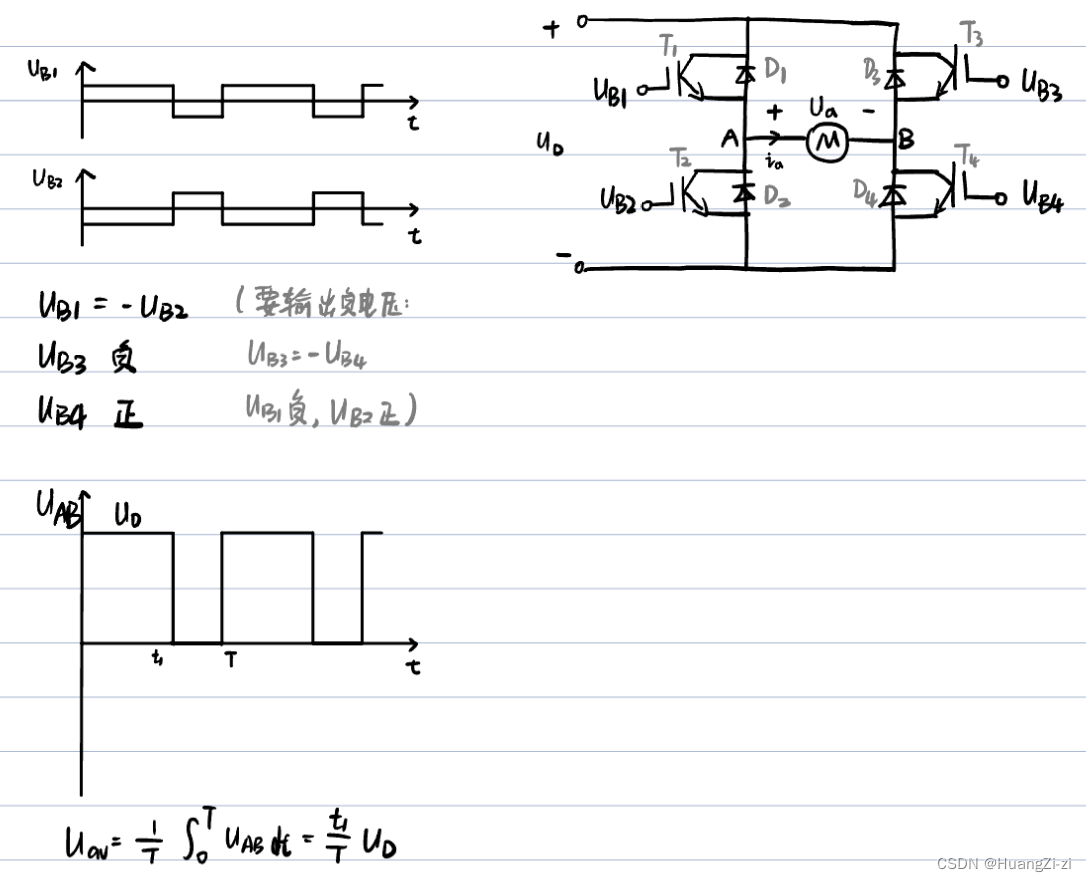
电动机状态
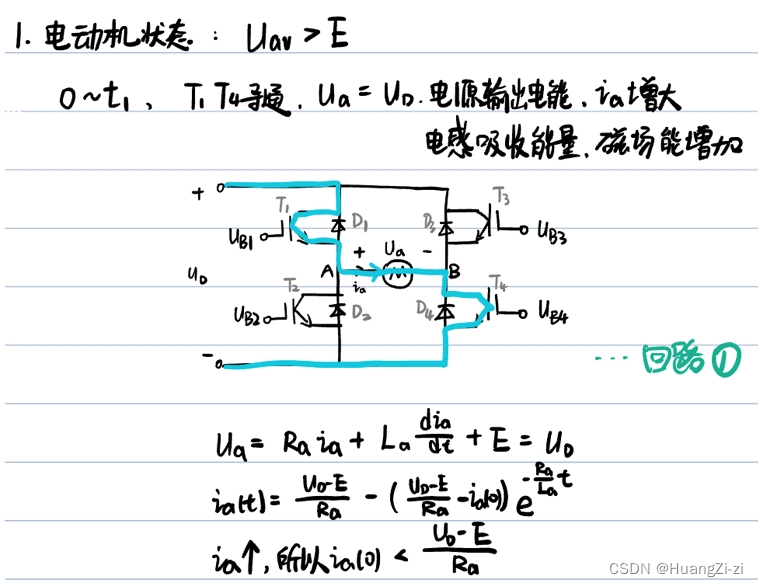

如果没有 D 2 D 3 D_2D_3 D2D3, T 2 T 3 T_2T_3 T2T3将被反向电压击穿 -
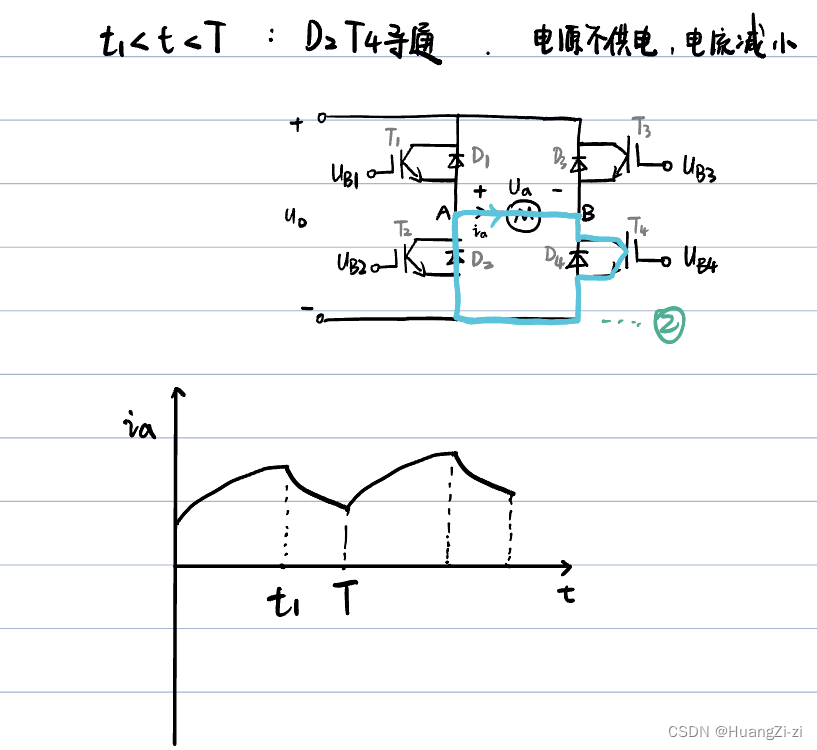
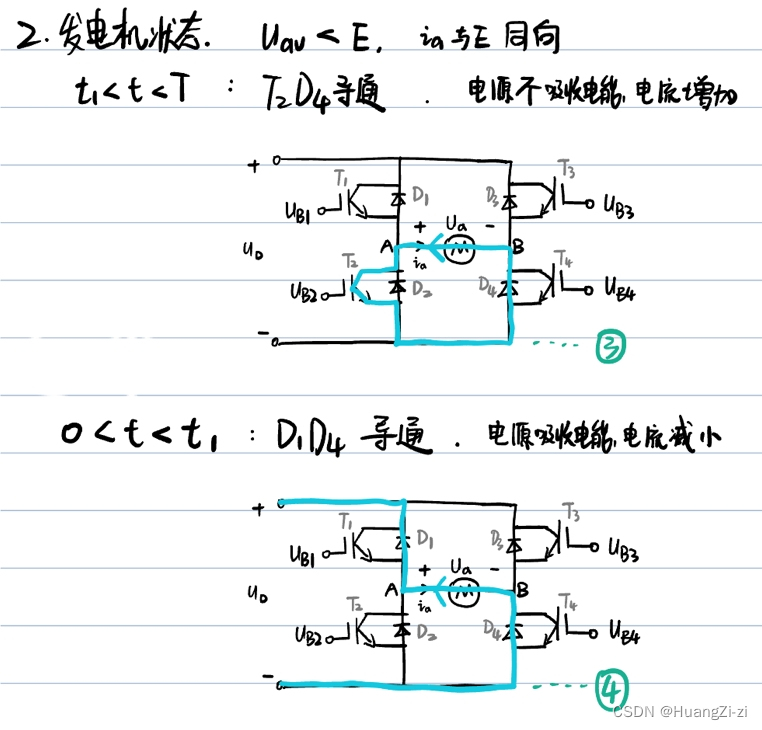
发电机状态
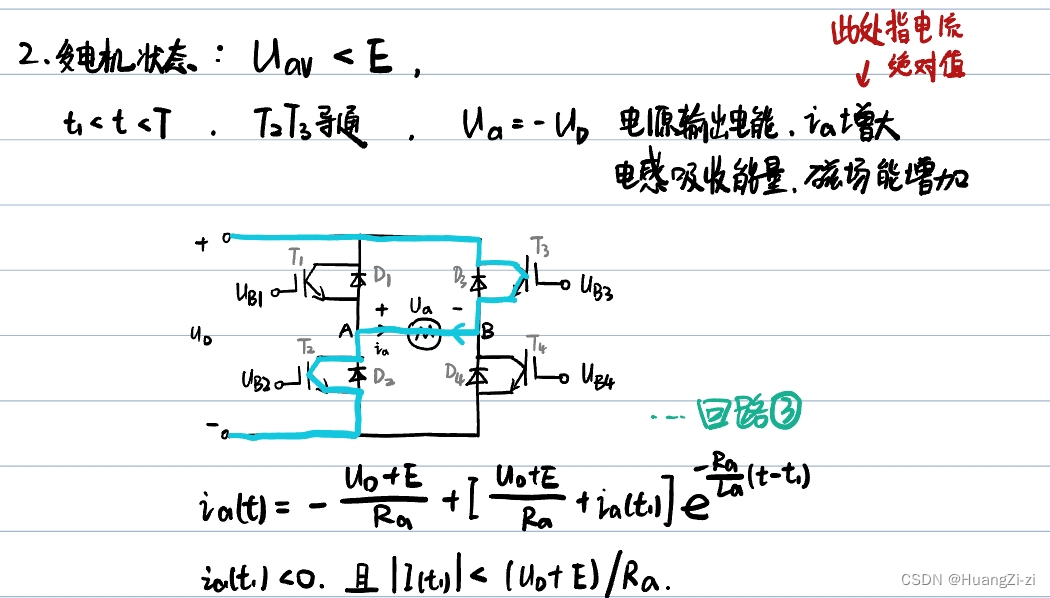
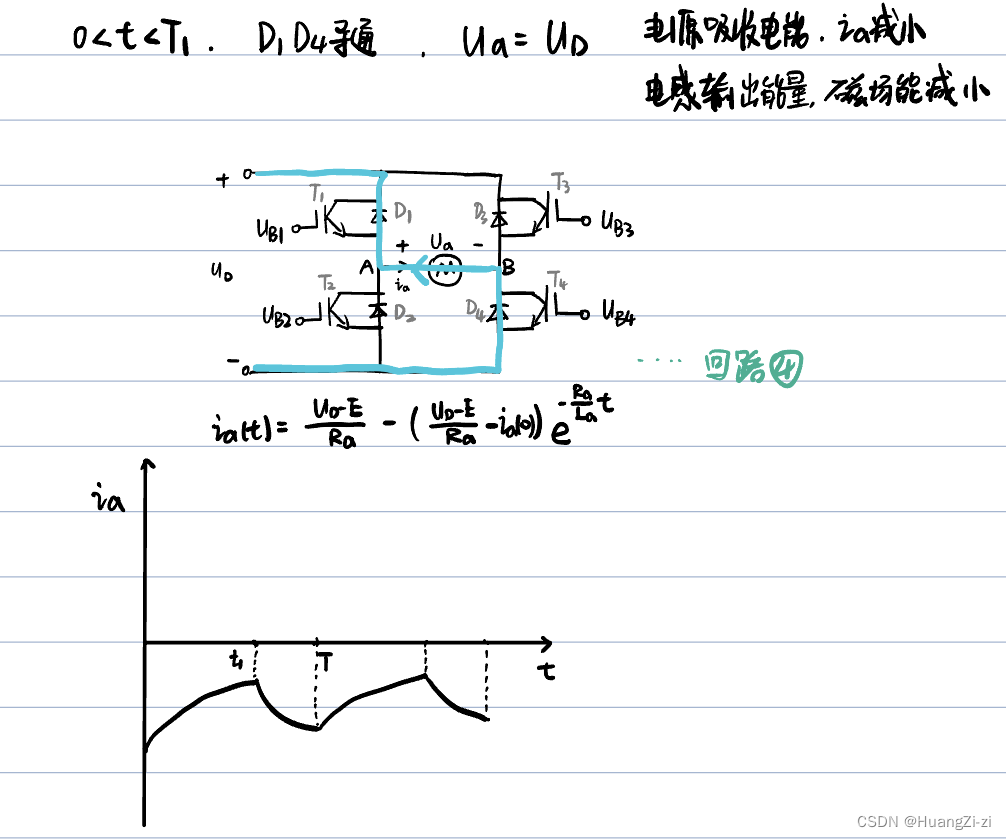
-
轻载状态
轻载:负载低于额定负载30%。功率因数低,带来电网污染。按照空载处理。

轻载是电磁转矩为0,电枢电压是交变脉冲电压,电枢电流是交变脉冲电流。虽然电流平均值为0,不产生转矩,但使得电机停转(E=0)时仍然有高频微震电流,从而消除正反转时静磨擦死区,起到动力润滑的作用。
- 总结
双极性输出一个周期中,输出电压为方波,有正负两个极性。电流连续,电流方向取决于电机工作状态
电机工作状态可逆,电机可以在四象限工作
欲反转,调整PWM信号占空比,使平均电压为-
单极性输出
只有一组IGBT输入PWM信号,另一组一个导通一个截止
-
电动机状态

-
发电机状态

-
轻载状态

- 总结
单极性输出,输出电压为方波,一个周期只有一个极性
持续有一个管子导通、一个管子截止,无法频繁地交替导通,因此输出损耗比双极性输出小,装置可靠性提高
输出电流无高频微震,启动速度较慢,低速性能不如双极性输出
有限单极性输出
不管是双极性输出还是单极性输出,都会出现在开关状态切换的过程中,两个管子同时导通,将电源短路的情况,称为共态直通
为了避免共态直通问题,可以:
1.在驱动信号设置死区,使得两个管子的状态切换存在时间差
2.选择有限单极性输出
相比与单极性输出,有限单极性输出只有一个管子处于开关状态,与其同桥路的管子截止,另一桥路一个导通一个截止
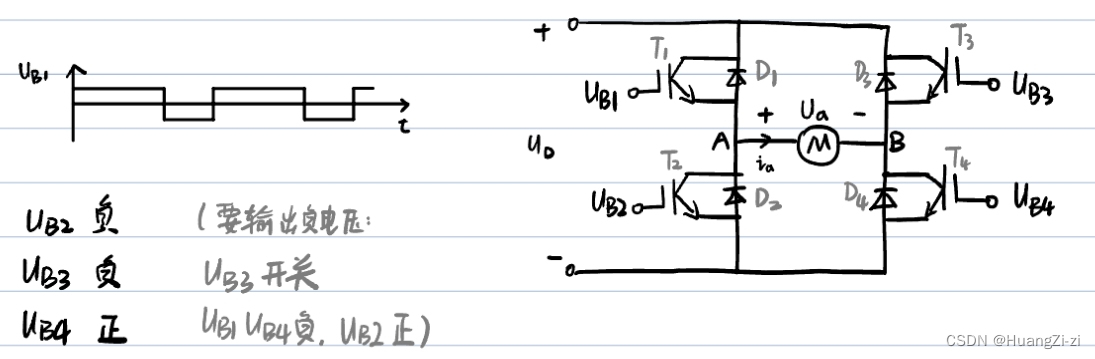
-
电动机状态
与单极性输出完全相同

-
发电机状态

-
轻载状态

电流降为0后,剩余的E不足以使 D 1 D_1 D1导通,因此电路短路,电流断续,影响快速性
PWM放大器的特性
-
信号系数: ρ = u i ∣ U i m ∣ \rho=\displaystyle \frac{u_i}{|U_{im}|} ρ=∣Uim∣ui,输入信号瞬时值与输入电压最大值之比
-
PWM信号参数:周期 T k T_k Tk,正向电压宽度 t 1 t_1 t1,占空系数 γ = t 1 T k \gamma=\displaystyle \frac{t_1}{T_k} γ=Tkt1
- 静态特性:
- 双极性输出:

t 1 = 1 2 T k ( 1 + ρ ) t_1=\frac{1}{2}T_k(1+\rho) t1=21Tk(1+ρ)或 γ = 1 2 T k ( 1 + ρ ) \gamma=\frac{1}{2}T_k(1+\rho) γ=21Tk(1+ρ) - 单极性输出: t 1 = ∣ ρ ∣ T k t_1=|\rho|T_k t1=∣ρ∣Tk或 ρ = ± γ \rho=\pm \gamma ρ=±γ
- 双极性输出:
- 动态特性:晶体管存在开启时间和关闭时间,可以看作延时环节
G ( s ) = Γ ( s ) U i ( s ) = K e − τ s \displaystyle G(s)=\frac{\Gamma(s)}{U_i(s)}=Ke^{-\tau s} G(s)=Ui(s)Γ(s)=Ke−τs
一般延迟都很小,不超过开关周期的一半。
在直流电动机控制系统中,由于PWM的开关频率是电机通频带的几百上千倍,因此认为可以忽略延迟时间,等效为比例环节
- 静态特性:
-
输出电压
-
双极性输出:

-
单极性输出:

-
在直流电机中:高频交流电频率远超电动机通频带,可以认为完全被衰减,因此PWM放大器可以等效为比例环节。
-
-
输出电流的平均值
直流电动机电枢两端的电压: u a = R a i a + L a d i a d t + E u_a=R_ai_a+L_a\frac{\rm d i_a}{\rm d t}+E ua=Raia+Ladtdia+E
电流是周期性变化的: I a v = U a v R a − E R a = I s ρ − I x I_{av}=\frac{U_{av}}{R_a}-\frac{E}{R_a}=I_s\rho-I_x Iav=RaUav−RaE=Isρ−Ix
其中: I s = U D R a I_s=\frac{U_{\scriptscriptstyle D}}{R_a} Is=RaUD(启动电流\堵转电流) I x = E R a I_x=\frac{E}{R_a} Ix=RaE(反电势电流) -
电流的脉动量
设一个周期内电流的最大值为 i a m a x i_{a\ max} ia max,最小值为 i a m i n i_{a\ min} ia min
则脉动量: Δ i = i a m a x − i a m i n = A I s γ ( 1 − γ ) τ e f k = A U D ( 1 − ρ 2 ) 4 L a f k \displaystyle \Delta i=i_{a\ max}-i_{a\ min}=\frac{AI_s\gamma(1-\gamma)}{\tau_ef_k}=\frac{AU_D(1-\rho^2)}{4L_af_k} Δi=ia max−ia min=τefkAIsγ(1−γ)=4LafkAUD(1−ρ2)
其中A:单极性时为1,双极性时为2
当信号系数 ρ = 0 \rho=0 ρ=0时脉动量最大
物理解释:电流曲线上升的快慢取决的电磁时间常数 τ e \tau_e τe。 f k f_k fk决定了上升和下降的时间。
























 4466
4466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








