2020年全国研究生数学建模竞赛华为杯D题无人机集群协同对抗求解全过程文档及程序

2020年全国研究生数学建模竞赛华为杯

D题 无人机集群协同对抗

原题再现：

  新一代人工智能技术和自主技术快速走向战场，将催生新型作战力量，颠覆传统战争模式，未来战争必将是智能化战争。无人机集群作战作为智能作战的重要形式，正在崭露头角。通过多架无人机协同侦察、协同探测、协同跟踪、协同攻击、协同拦截等，共同完成较复杂的作战任务。
  现考虑红、蓝双方的无人机集群在平面区域内的协同对抗问题。蓝方作为进攻方，希望突破红方无人机的拦截，成功抵达目的地遂行军事行动；红方则希望在给定的区域内完成对蓝方无人机的拦截，阻止蓝方的突防。本赛题讨论的对抗区域约定为图1所示的矩形区域 ，攻击纵深即 之间的距离为 ，蓝方无人机的飞行轨迹不能越过 、 两边，即考虑的是攻击通道（突防走廊）带宽有一个限定约束的情形，通道带宽即 之间的距离记为 。蓝方无人机的速度为 ，最小转弯半径为 ；红方无人机的速度为 ，最小转弯半径为 ；红蓝双方无人机的速度保持不变，运动的方向可根据机动策略的需要随时改变，但受转弯半径的限制。

  本赛题只讨论平面上的红蓝双方对抗问题，即红蓝双方的无人机均在同一高度上机动飞行。双方无人机均装载有探测装置和数据链，能够准确探测对方无人机和己方无人机的实时位置。鉴于蓝方无人机在机动速度上具有优势，红方考虑通过多无人机的协同，即通过数量上的优势部分弥补性能上的劣势，以提高己方的对抗效果。红方执行拦截任务的无人机由运载机携带至攻击位置，然后根据对抗需要发射一定数量的无人机，组成无人机集群与蓝方突防无人机对抗。如图1所示的对抗状态，红方为阻止蓝方无人机的突防，分别由运载机 和 各发射5架无人机组成两个无人机集群遂行拦截任务。当蓝方突防无人机与红方至少2架无人机的距离均小于 时，就认为红方成功拦截了蓝方突防无人机。同时，根据任务要求，蓝方无人机需在 内越过边界 ，否则视为突防失败。红蓝双方都想充分利用自身的优势，通过运用最优机动策略以实现突防与拦截的目的。
  红方无人机集群可以根据实际需要进行编队飞行，如图2所示，红方无人机集群采用了其中的一种队形，5架无人机位置近似分布在一个圆周上，任何相邻两架无人机的间距相同。为控制、通信以及相互避撞的需要，要求红方任何两架无人机的间距需大于 ，每一架无人机与本集群中至少两架无人机的距离不超过 。红方运载机与所属无人机集群中至少一架无人机的距离不超过 ，与任何一架无人机的距离需大于 ，同时为安全需要，与蓝方的突防无人机的距离需大于 。红方运载机的速度为 ，转弯半径不小于 。红方运载机和无人机的飞行轨迹不受边界的限制。

  为叙述方便，运载机FY01发射的无人机编号记为FY01××，因此图2中5架无人机编号分别记为FY0101、FY0102、FY0103、FY0104、FY0105。运载机FY02发射的无人机编号记为FY02××，其余类推。无人机集群初始时刻的位置分布采用位于一个圆周上均匀分布。实际中，运载机布设无人机集群需要一定的时间，为简化计，本赛题暂不考虑这一时限，可视为瞬间布设好无人机集群，且满足相关约束条件。在对抗过程中不要求全程按照某一固定队形飞行，可根据需要随时调整队形。
  请你们团队通过建立数学模型，研究下列问题：
  问题1 如图3所示，对抗伊始红方2个无人机集群的圆周中心分别位于G1和G2，圆周半径为100m，其中DG1=20km，G1G2=30km，CG2=20km。试建模分析蓝方无人机处于矩形区域ABCD内哪些位置时，无论红方无人机采用什么样的追击策略，蓝方无人机总能采用合适的策略以躲避红方的拦截，实现成功突防；讨论蓝方无人机相应的最优突防策略。

  问题2 如图4所示，对抗伊始蓝方突防无人机位于边界AB的中心点，红方2个无人机集群的圆周中心分别位于G1和G2，圆周半径为100m，其中G1和G2位于边界CD上，具体位置根据需要确定。试建模分析是否存在一个通道带宽M的下限M_min，当实际通道带宽M比M_min大时，蓝方无人机一定能突破红方无人机集群的拦截；给出此种情形下蓝方无人机时间最短的突防策略。

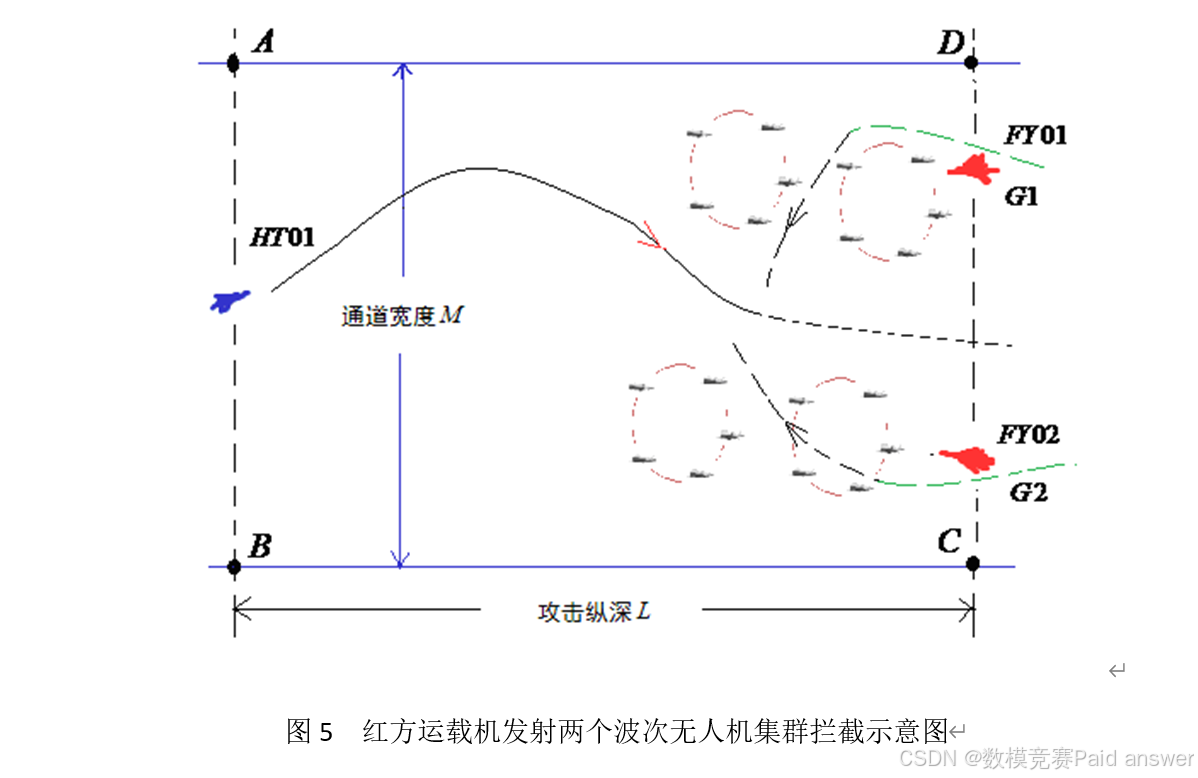
  问题3 红方每架运载机可分两个波次共发射10架无人机，组成两个无人机集群遂行拦截任务，每个无人机集群的无人机数量不少于3架。每一波次发射时无人机集群初始队形如图2所示的圆周构型，运载机与圆周中心的距离为2km，随后无人机集群的队形可根据需要调整，但要求满足相应的间距约束。如图5所示，对抗伊始，蓝方无人机位于边界AB的中心，通道带宽M=70km；红方两架运载机分别位于边界CD上G1点 和G2点，并开始发射第一波次的无人机集群，运载机和无人机集群中心具体位置根据需要确定。运载机第二波次发射无人机集群时，必须保证运载机与第一波次发射的无人机集群满足间距上的约束。讨论红方两架运载机两个波次发射的无人机数量、每架运载机第二波次发射的时刻和位置以及第二波次发射的无人机集群的中心位置，以实现最优的拦截效果；进一步具体建模分析是否存在一个通道带宽M的上限M_max，当实际通道带宽M小于M_max时，无论蓝方无人机采用什么样的突防策略，红方无人机集群均存在相应的拦截策略，在区域ABCD内成功阻止蓝方无人机的突防。

  问题4 如图6所示，通道带宽M=100km，蓝方3架突防无人机组成突防集群从矩形边界AB一侧开始突防（任2架突防无人机的间距需大于30m），红方5架运载机各携带10架无人机，从边界CD一侧同时开始遂行协同拦截任务。红方每架运载机分两个波次发射无人机，分别组成两个无人机集群，每个集群的无人机数量不少于3架；每架运载机第一波次发射无人机的时刻为初始对抗时刻，与所属无人机集群几何构型圆周中心的距离为2km。红方运载机初始位置、红方运载机发射的第一个波次的无人机集群中心位置、红方运载机发射第二波次无人机集群的时刻和位置、第二波次发射的无人机集群中心位置、两个波次无人机数量以及蓝方突防无人机初始位置根据需要确定。蓝方希望尽可能多的无人机突防成功，红方则希望成功拦截尽可能多的蓝方无人机。试讨论红方最优拦截策略和蓝方最优突防策略。

整体求解过程概述(摘要)

  本文对无人机群集群对抗任务进行了分析研究，针对每个具体问题建立模型并采用合适的算法进行求解。
  问题一第一小问为定性微分对策问题，在完全信息以及最优策略的基础下求解蓝方的可逃脱区域等同于求解定性微分对策的界栅问题。根据题目首先建立了地面坐标系和航迹坐标系，根据题目建立运动与位置约束条件。对无人机可行队形进行分析，并计算出近似最大覆盖面积用于确定边界。基于双机编队的队形确定了坐标系的转换关系，把微分对策看作变分问题，进而利用极大值极小值原理构建哈密顿函数解最优控制，椭圆控制集将引起奇异解，将初始值以及求解的最优控制代入运动方程倒向积分可得最优轨线，最优轨线构成界栅。由BUP （目标集的可用部分边界）为起点所构成的界栅与NUP 所围成的区域构成了对策空间的躲避区。
  问题一第二小问在第一小问的基础上求解蓝方最优突防策略，即该微分对策问题的纳什均衡。博弈理论中的动态博弈与矩阵对策相结合的方法，选取目标规避策略中有限种机动形式的组合作为策略集，根据红蓝双方距离以及追逃时间为量化指标建立支付函数，由哈密顿函数求取动态博弈模型的纳什均衡解，得出了受初始值位置影响动态突防策略。 问题二为生存型定量微分对策问题，在问题一的基础上建立双机编队下时间最优的无人机突防模型，其中支付函数以逃脱时间为量化指标。当通道带宽取下限时，蓝方出发点（AB中点）位于界栅上。由于问题解析求解过于复杂，将突防区域进行栅格化划分并根据条件约束进行航迹优化，运用蚁群算法进行不同初始值下的的纳什均衡解，并反推出通道宽度极限值。根据计算结果分析红方出发位置对蓝方初始局部区域哈密顿函数的影响，得到红方最优的发射点分布。仿真分析不同通道宽度下蓝方出发点的哈密顿函数值，得到通道宽度取值为92.2Km。
  问题三，红方运载机可以发射两个波次的无人机，即基于微分对策理论研究二维空间内多对一无人机突防模型，求取突防模型中拦截过程的发射策略（数量分配、路径规划）。分为三步求解：基于博弈论的飞行器微分制导律方法建立多对一拦截模型，运用零脱靶量建立支付函数，此处，以飞行器拦截目标为背景，借鉴滚动时域控制的思想，构建动态博弈模型；第二步运用快速随机数算法进行动态最优策略的搜索，规划追捕过程的最优路径；第三步为了简化动态搜索过程、提高搜索精度，采用Dubins方法对栅格化路径中转弯最优角度进行判断，RRT算法评价对路径选择及计算效率的影响。求解可得最优拦截策略（表6-2）以及任意情况成功拦截的通道带宽上限值为108.8Km。
  问题三第二问通道带宽上限是否存在的问题，即生存型微分对策的鞍点存在性问题。根据微分对策最优性条件推导该问题对策鞍点满足的必要条件，哈密顿函数中双方极值存在，并利用差分进化算法进行求解。
  问题四为多对多无人机对抗最优策略问题。分四步进行模型的求解：第一步建立无人机集群的协同对抗模型；第二步建立突防区的空战态势优势函数，根据红蓝双方的态势信息如几何位置计算对抗区域边界，对空战态势进行评估；第三步运用分布式一致性拍卖算法（CBAA）对目标进行分配决策，对整个集群的目标函数进行优化；第四步基于SAC-OD规则进行集群运动决策，基于集群动态拓扑交互机制，建立有限感知条件下的集群运动模型，使