浅谈EbN0与SNR——从数字通信设计角度

引言：很多初学者在学习通信原理的时候会先从SNR入手接触AWGN信道，然后进行误码率的MATLAB仿真。但是可能在深入学习的过程中会迷惑SNR和$E_b{N}_0$的关系，尤其是接触扩频通信的时候。
本文尝试从$E_b{N}_0$的定义入手，推导$E_b{N}_0$与SNR的关系，浅谈两者在数字通信中的意义。

什么是SNR与EbN0？

在模拟通信领域，信号平均功率和噪声平均功率的比值被定义为信噪比(Signal To Noise Ratio, SNR)。

然而在数字通信系统中，我们通常使用信噪比的归一化形式$E_b{N}_0$作为性能指标。$E_b$为每bit的能量，等于信号平均功率$S$乘以每bit持续时间$T_b$，$N_0$为噪声功率谱密度，等于噪声功率与带宽$W$之比。

所以有
$$\frac{E_b}{N_0}=\frac{S{T}_b}{N/W}$$
考虑到每bit持续时间$T_b$等价于bit速率$R_b$的倒数，所以有
$$\frac{E_b}{N_0}=\frac{S{T}_b}{N/W}=\frac{S/R_b}{N/W}=\frac{S}{N}(\frac{W}{R_b})$$

误码率与EbN0

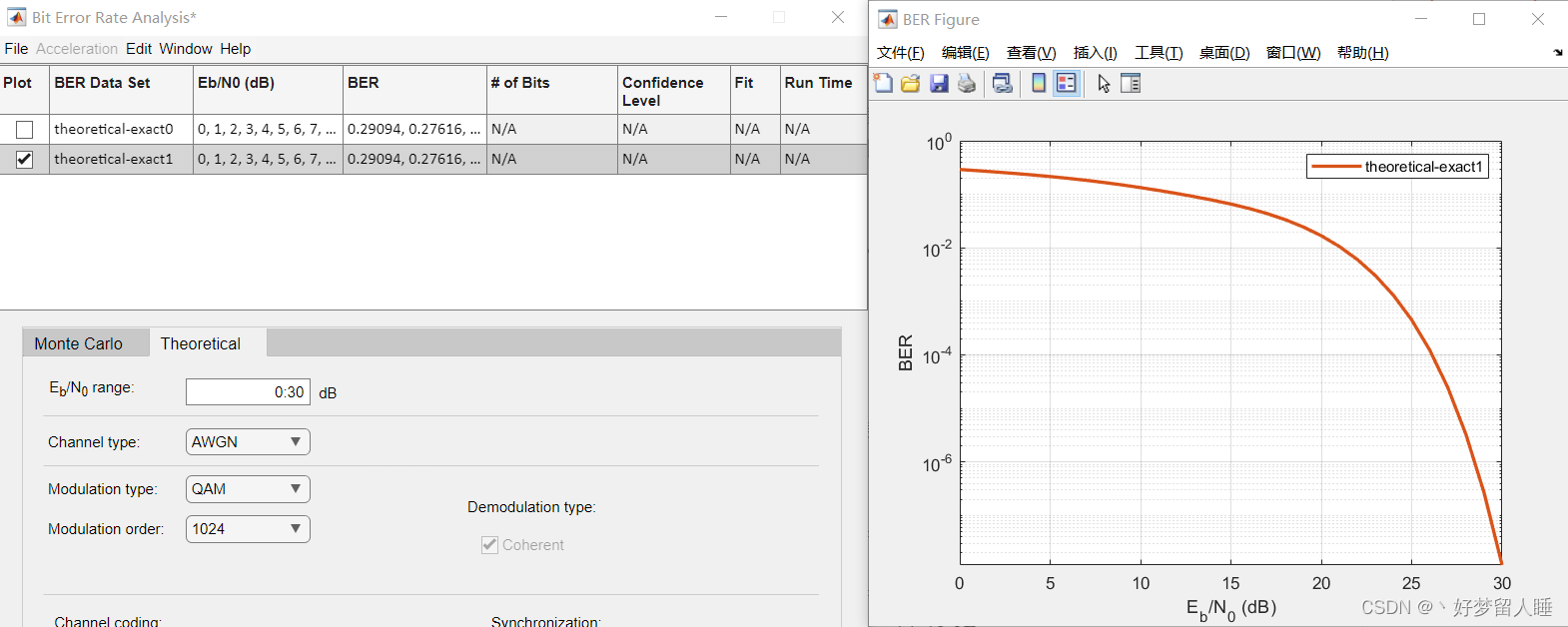
数字通信中最重要的度量之一就是误码率$P_b$和$E_b{N}_0$的关系曲线，在MATLAB中我们可以使用bertool工具箱计算不同$E_b{N}_0$下的误码率$P_b$。如下图所示。

关于误码率和EbN0的关系有很多教材都有非常详细的介绍，这里推荐goldsmith的wireless communication的第六章关于数字通信的性能分析这一章，可以作为详细阅读材料。

但是有一个问题就来了，我们在MATLAB中使用的加噪函数y=awgn(x,SNR,'measured')接收的参数是SNR，但是我们在理论分析的时候使用的是EbN0，这两者该怎么转换呢？为什么不用SNR而要用EbN0呢？接下来我将尝试用一个简单的例子来解答以上疑问。

小小总师历险记

用什么调制方式

2014年12月，美国联邦通信委员会(Federal Communication Committee,
FCC)举行的第96场频谱拍卖会中，LTE Band 66频段，2.1GHz，总带宽10MHz，以449亿美元的价格成功拍卖。

作为通信系统设计师的你，被老板安排了一个任务，在这个10MHz带宽上实现一个收发距离30m的100Mbps吞吐量的通信系统，要求误码率1e-6。

请问你该如何实现呢？请先别急着往下寻找答案，先思考一下，你该如何设计这样一个系统来实现老板的要求呢？

当然不是让你直接给出方案啦，首先让我们一起先思考一个最简单的问题，用什么调制方法？BPSK可不可以？QPSK呢？16-QAM可以吗？如果要实现100Mbps的吞吐量，使用BPSK，我们该使用多大的模拟带宽呢？

这时你想到，模拟带宽和方波周期有关，对于BPSK，100Mbps对应着方波长度为$\frac{1}{100e6}s$，直接对应的频域为$sinc()$函数，对应的主瓣宽度为100MHz。如果我们要用BPSK实现，我们得需要100MHz的模拟带宽。

可是老板只买到了10MHz的带宽，难道你要去找老板说老板你再买90MHz的带宽来吧？老板看了看已经花掉的449亿美元，怕不是你当场就被炒鱿鱼了。

那没办法了，只好增加每个方波的长度了。你一算，对于10MHz的带宽，那么每个方波的长度就应该是$\frac{1}{10e6}s$，也就是说我需要将10个bit映射成1个方波。你找了找，最后发现还真有这种调制方式，1024-QAM ！于是问题解决了，你找到老板跟老板说，我们决定用1024QAM的调制方式，绝对满足老板您的需求。

发射功率和路径损耗

老板很高兴，大手一挥，那你就做吧，别忘了看功率发射要求，要不然政府不会允许我们产品上市的。于是你回去查了一下FCC和国家无线电管理委员会(State Radio Regulatory Commission, SRRC)的发射功率要求，一看EIPR为20dBm，我们就暂时不考虑那么多天线增益的事情了，就按照这个最简单的来算，发射功率为20dBm。

这时你就开始嘀咕了，这个20dBm对我有什么影响呢？30m的通信距离又有什么关系呢？

路径损耗(Path Loss, PL)就是我们下一步需要考虑的事情，20dBm的无线信号经过30m的传输之后，到达接收端时还有多少功率呢？感兴趣的同学可以翻阅一下其他资料，这里直接给出理想环境下的路径损耗的公式
$$PL(dB)=32.44dB+20lo{g}_{10}(F_{c}D)$$
其中$F_c$是载波频率，单位为MHz，$D$是发射机和接收机之间的距离，单位是km。这里我们使用2.4GHz的载波，所以有
$$\begin{array}{rl}PL(dB)& =32.44dB+20lo{g}_{10}(F_{c}D)\\ & =32.44dB+20lo{g}_{10}(2400\ast 0.03)\\ & =69.5866dB\end{array}$$
所以接收到的信号功率是$20dBm-69.5866dB=-49.58dBm$。你一看，完了，这么低，两眼一黑。

EbN0的计算

再回到我们最初介绍EbN0的计算，
$$\frac{E_b}{N_0}=\frac{S{T}_b}{N/W}$$
100Mbps的系统，也就是每bit对应时间为$\frac{1}{100e6}s$，$N_0$是-174dBm，那么我们最终的$E_b{N}_0$就是
$$\begin{array}{rl}\frac{E_b}{N_0}(dB)& =S+T_b-N_0\\ & =-49.58+10lo{g}_{10}(\frac{1}{100e6})+174\\ & =44.42dB\end{array}$$
然后我们再看看MATLAB的bertool中1024QAM的要求，误码率要求大概在27dB左右，我们有44dB，完全能做。

总结

上一章基本介绍了一个简单的数字通信的设计，当然我们还有很多细节没有考虑，路径损耗肯定不理想，要不要上编码改善性能降低发射功率？能不能压低频带占用率给其他应用提供资源？怎样改善通信QoS？能不能上升到500Mbps？后面还有很多需要考虑的东西，这才是一个数字通信的角度的EbN0的看待观点。