2022张宇考研基础30讲第十讲积分等式与积分不等式

最新推荐文章于 2024-03-02 21:40:58 发布

晴夏。

最新推荐文章于 2024-03-02 21:40:58 发布

阅读量1.7w

点赞数 8

分类专栏：考研数学

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_43757333/article/details/113803583

版权

考研数学专栏收录该内容

16 篇文章

订阅专栏

第十讲积分等式与积分不等式

在这里插入图片描述

在这里插入图片描述

积分等式

推广的积分中值定理
JJJJJJJJJJJJJJJJJJUUUUUUUUUUJJJJJJ

在这里插入图片描述
有些积分通过所学的方法是无法求解的，此时可能需要一些特别的方法或者是题目的提示
例如下面这个需要使用放缩

用夹逼准则
在这里插入图片描述

在这里插入图片描述
当见到极限号后面有积分号的时候想到用夹逼准则（注意先积分再算极限不可交换顺序）

积分不等式

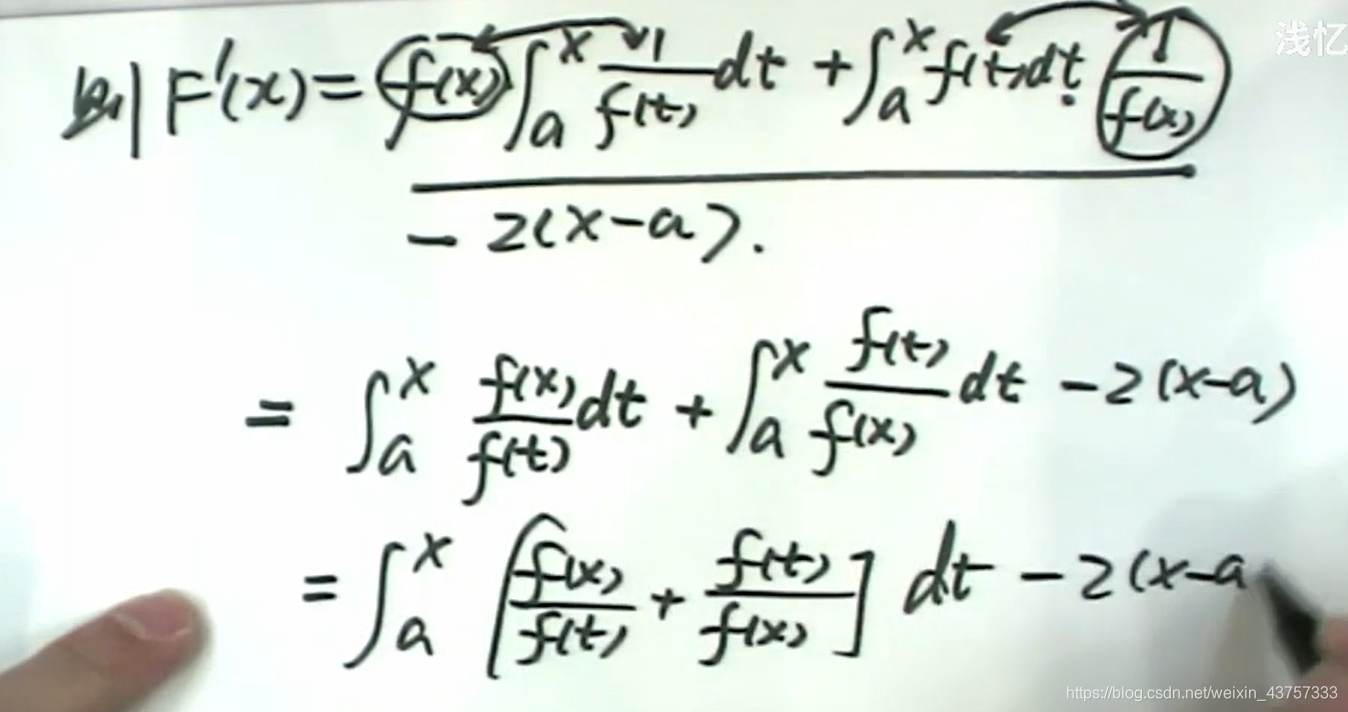
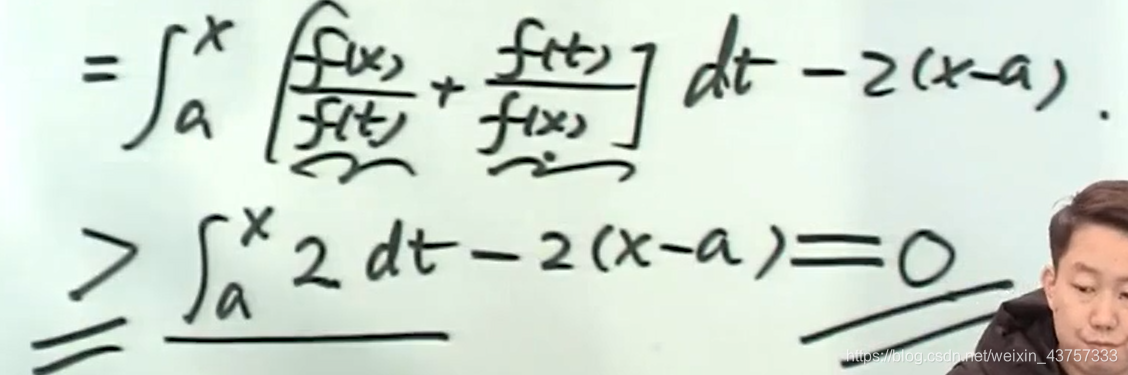
在这里插入图片描述

在这里因为不可能一直满足恒等的条件
所以一直恒大于零

在这里插入图片描述

某函数一阶可导不代表它的导数连续例如振荡间断点的情况

在这里插入图片描述

在这里插入图片描述
由拉格朗日可以实现从f到f‘的转化

所以上图最后一步由于需要将题目所证的不等式从左往右推，所以此时将f转换f’

而我们知道
在这里插入图片描述
红框中的东西其实就是类似介值定理中的最大值
那么|f’(x)|肯定也小于这个东西
所以在这里就继续放缩成这个东西就得到

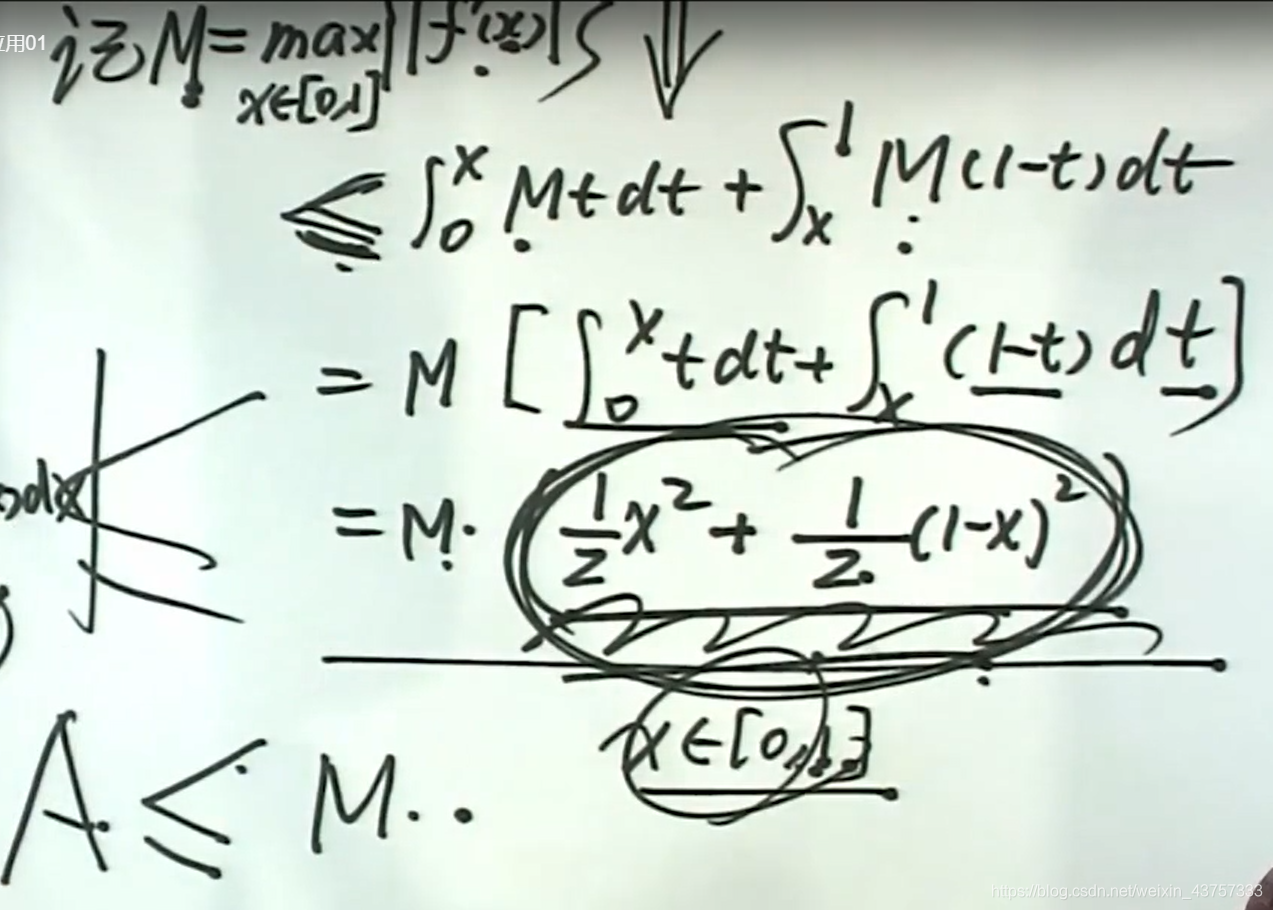
在这里插入图片描述
而根据下面这个不等式

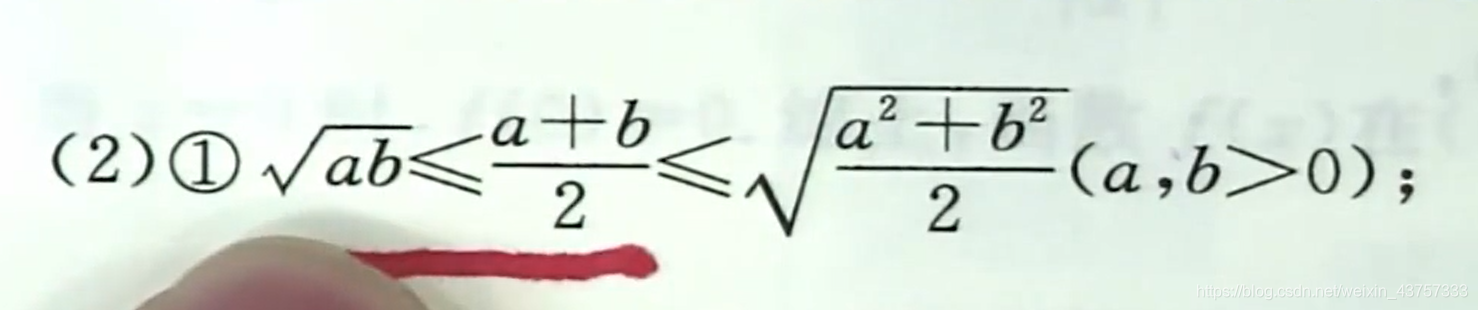
在这里插入图片描述

所以这玩意是大于等于（x+1-x）²/4也就是四分之一

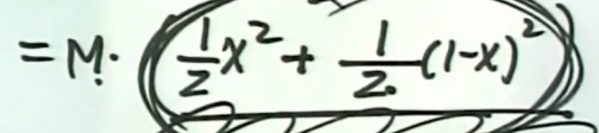
在这里插入图片描述
那么现在，不等式的左边小于等于这个东西，也就是说小于等于这个东西的最小值，而这个东西的最小值是四分之一
所以也就是说不等式左边小于等于M/4
那么题目得证

（这里其实有一个逻辑没理得太顺：
一开始都是连续的小于等于号：
在这里插入图片描述
但是最后的这玩意要用到的公式却是大于等于某个数：

这里你可以这样理解
比如需要证明gx<=2
如果gx<=fx 而fx的最大值都<=2的话
那么肯定就可以得出gx<=2

但是另外一个思路
而如果我们能证明出gx<=fx
并且如果fx的最小值如果是2的话，那么只要gx<=fx，也就可以证明gx<=2了

所以其实如果已知gx<=fx，欲证gx<=2

如果fx的最大值是2，那么可以证明出来gx<=2
如果fx的最小值是2，那么可以证明出来gx<=2

这其实意味着在连续的放缩中（例如上题中的连续小于等于），在一系列放缩的途中，中间都必须是小于等于号，而最后一步，可以是大于等于号，也可以是小于等于号，如图所示：

在这里插入图片描述
那么以下两种情况都可以

在这里插入图片描述

第一题采用分部积分

我们知道反对幂指三中
如果是具体的函数知道它适合积分或者不适合
但是如果是抽象函数我们无法知道它适合还是不适合积分此时命题老师就会给提示

例如本题中
在这里插入图片描述

下一道例题：

在这里插入图片描述
所以这一题的思路是：

而那慕达小于1，所以只需要证明FX是单调递减的就可以了

在这里插入图片描述
其实这个东西就是平均值

在这里插入图片描述

在这里插入图片描述

这里是等式而不是求导

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。