【L4】深蓝学院-高飞老师 移动机器人规划笔记 动力学约束下的路径规划

---

传送门
【L3】深蓝学院-高飞老师 移动机器人规划笔记 基于采样的最优路径规划算法&进阶
【L2】深蓝学院-高飞老师 移动机器人规划笔记 基于搜索的路径规划
【L1】深蓝学院-高飞老师 移动机器人规划笔记

---

前言

Q1: 首先，为什么要kinodynamic呢，也就是考虑运动学和动力学（后续简称为动力学）呢？
因为在现实世界中的机器人，他们是有自己的运动模型的，仅仅将他们转化为质点考虑运动路径肯定是有失偏颇的。
Q2: 当然，前面其实提到过，在整个pipeline中，还有后端做轨迹优化的部分，会考虑到机器人的动力学，那在前端为什么要考虑动力学这个事情呢？
简单来讲，这样去做可以降低后续后端路径优化的负担。而且，后端优化的时候，往往都是在局部进行优化，如果前端完全不考虑动力学的话，可能会产生对于机器人来说动力学代价更大的路径。

---

小例子

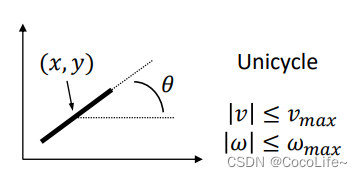
自行车

一般比较简单，输入就是速度和角速度，
$\left(\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right)=\left(\begin{array}{c}\cos \theta \\ \sin \theta \\ 0\end{array}\right)\cdot v+\left(\begin{array}{l}0\\ 0\\ 1\end{array}\right)\cdot \omega$
约束就是速度和角速度的最大值，

差速驱动机器人

$\left(\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right)=\left(\begin{array}{c}\frac{r}{2}\left(u_l+u_r\right)\cos \theta \\ \frac{r}{2}\left(u_l+u_r\right)\sin \theta \\ \frac{r}{L}\left(u_r-u_l\right)\end{array}\right)$
类似的约束，

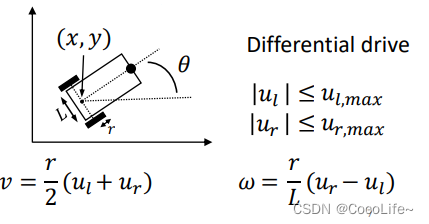
这几个比较经典的动力学模型网上的教学还比较多，随便挂一个差速驱动和自行车模型的二维运动学模型。

---

方法

状态栅格搜索算法：State Lattice Search

前面的基于采样的、基于图搜索的方法都有一个共同需要关注的问题，那就是搜索树的构建问题，然后就可以用各类的图搜索的方法解决问题。但是在之前的方法中，我们都默认机器人是一个质点，它可以向各个方向移动，但是现在就需要一个节点之间的可以给机器人进行执行的feasible motion connection 而不是之前的直接连接。
有两种思路去实现这样的建图（边）：

• 正向-离散化控制空间：驱动机器人运动得到feasible motion connection。
• 反向-离散化状态空间：找到机器人周围的很多个状态，找到当前状态到某个状态的连接。

对于一个机器人的运动模型：$\dot{s}=f(s,u)$，即状态s的导数是一个由状态和输入为变量去描述的函数。一般会给一个初始状态$s_0$。

对应上面的两种思路，

• 离散化控制空间：给系统不同的u，并保持一定的时间，看系统在不同的激励下会变成什么样子。前向仿真，易于实现，有点类似djisktra算法，没有目的性的扩展，容易造成较低的效率。
  
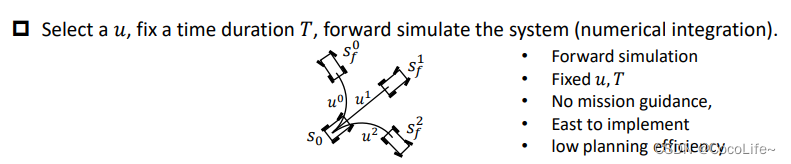
• 离散化状态空间：给定状态，从两个状态之间解析运动的边（解出u和T），看什么样的u和T能让机器人从一个状态到另外一个状态。反向的计算，比较难实现，但是自然地具备heuristic的效果。

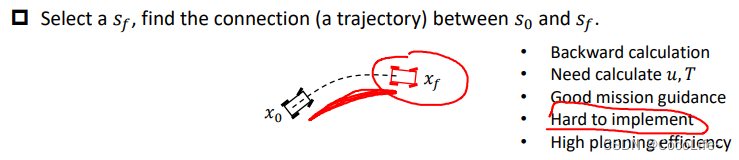
在控制空间采样的示例

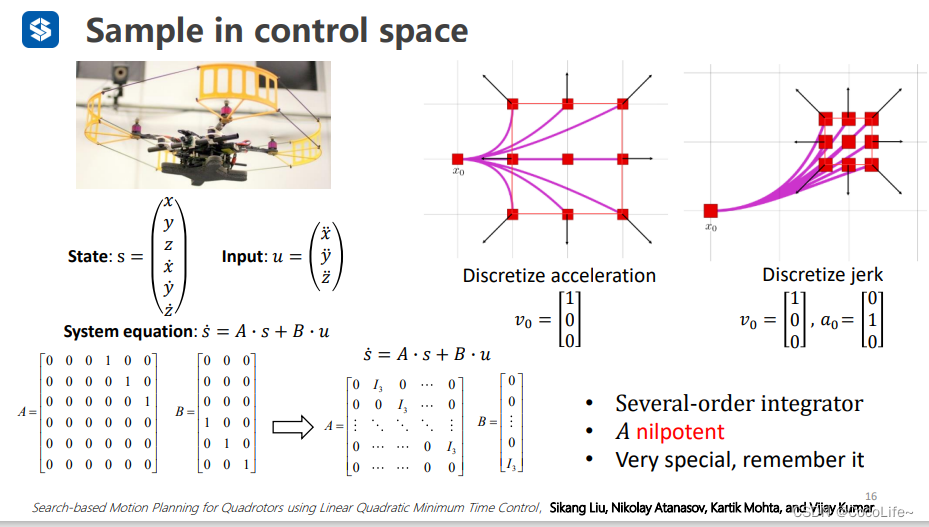
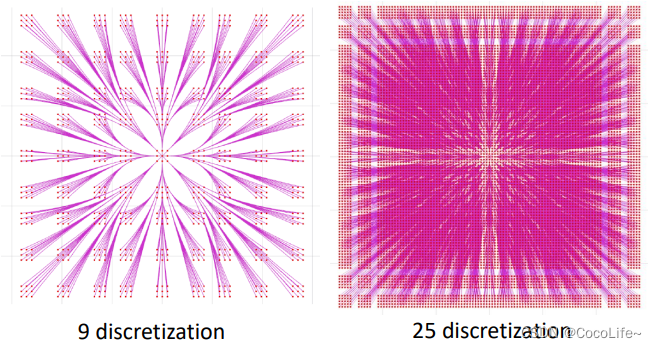
用位置和速度作为状态$s$，用加速度作为输入$u$，构成一个线性系统方程：$\dot{s}=A\cdot s+B\cdot u$。（再往高阶的话，也可以用三阶导jerk作为输入，状态填入加速度的三个维度）。中间的图即表明了，在以加速度为输入的情况下，以[1，0，0]作为初速度，选取不同加速度后经时间t后得到的离散的控制空间的点。右边的图就是用jerk作输入的结果。不断进行这个过程就会得到lattice graph，如下所示，但是其实不用把整个lattice graph建完再搜索路径（因为这个图与前面用的已经构建好的栅格图不一样，这个图最开始是没有的），可以利用heuristic函数类似的思路去提高效率。

需要注意一下，上面系统方程中的A矩阵，叫做nilpotent，即幂零矩阵，这个矩阵的性质很适合去除展开式里的高次项，方便我们求解。

具体来说，给定sample后，可以根据系统方程输入计算最后的末状态（给定输入和时间），驱动系统向前前进，那怎么确定中间的轨迹呢？这就涉及到了如下的状态转移方程：
$s(t)=\underset{F(t)}{\underbrace{e^{At}}}{s}_0+\underset{G(t)}{\underbrace{\left[{\int }_0^t{e}^{A(t-\sigma )}Bd\sigma \right]}}{u}_m$

简单来讲，就是状态$s$随时间变化的函数，是与初状态和整个过程中选取的控制量有关的。前半项是零输入响应，后半项是零状态响应。如果给定时刻$t$，一般对$e^{At}$做展开计算，$e^{At}=I+\frac{At}{1!}+\frac{(At{)}^2}{2!}+\frac{(At{)}^3}{3!}+\cdots +\frac{(At{)}^k}{k!}+\cdots$，这样A矩阵作为幂零矩阵就很有作用了。

对上述的整个过程举一个简单的小车模型的例子，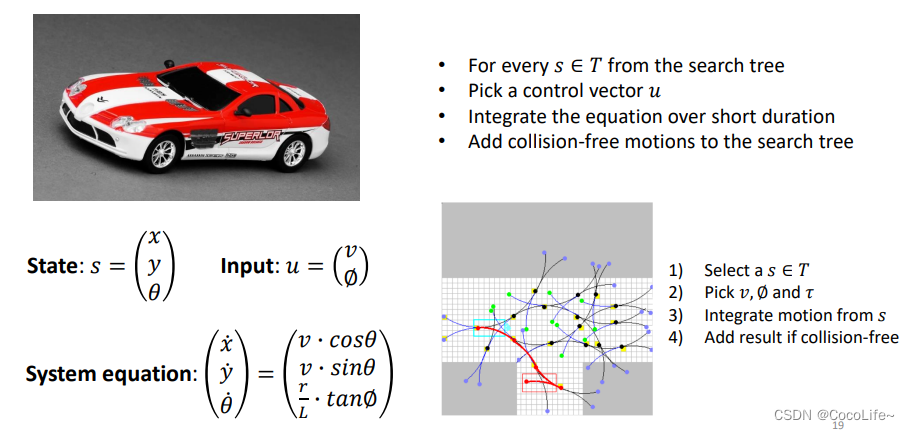

在状态空间采样的示例

如下图所示，给定一个初始的状态，先离散出他周围临近的状态，然后反推状态之间的可行性路径。

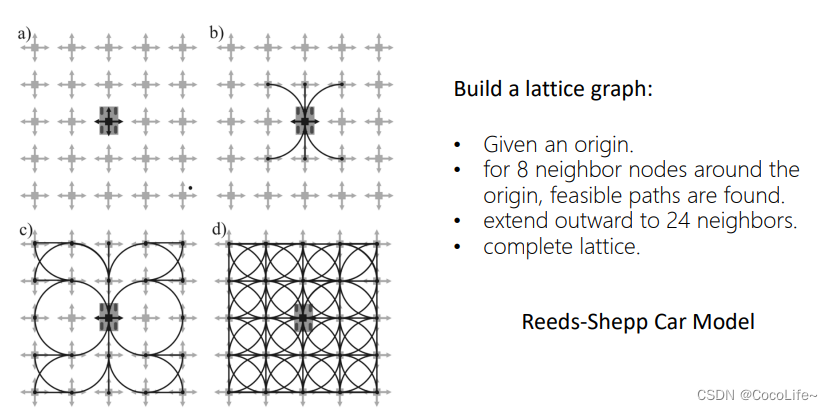
下面图展现了，两者比较直观的对比，

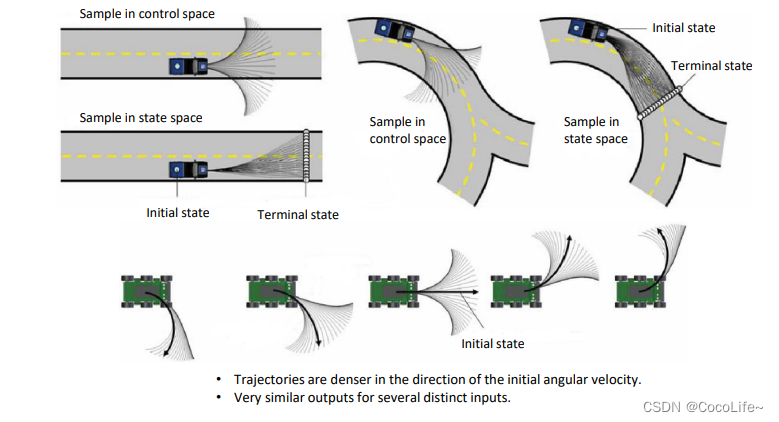
看起来，状态空间采样的方法要好一些，因为不会出现那些失败的路径。而且如果控制空间的输入变化的范围控制不好的话，可能会导致一系列的路径都容易是失败的，因为他们比较接近。那为什么不完全使用状态空间采样的方法呢，原因在于其实现的难度。下面介绍一下，已知起点终点状态，怎么去解中间的可行路径的一个方法。

Boundary Value Problem （BVP）

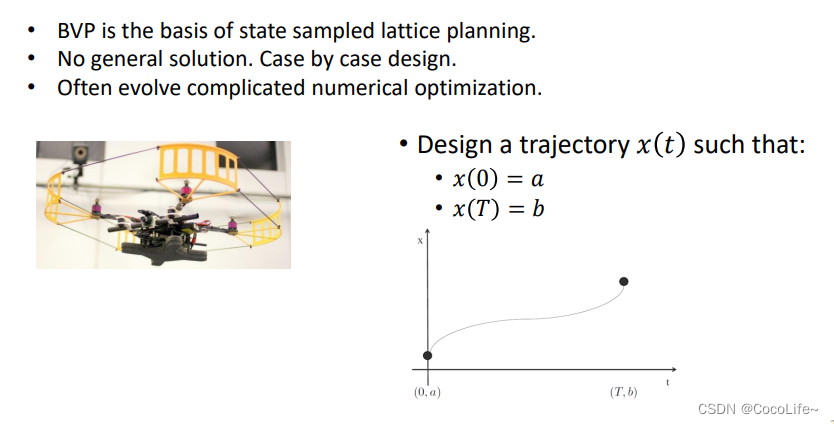
比如，以x轴方向为例，可以用多项式做参数化，

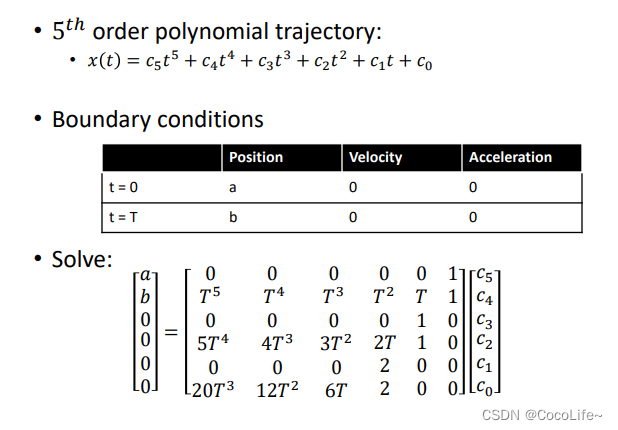
以上可能有很多解，因为限制条件比较少，获得一个解相对而言比较容易，但是获得比较优的解还需要其他的方法。

Optimal Boundary Value Problem （OBVP）

任务：给定初始和终点两个状态，我们想要去找到中间的最优$s^{\ast }$和$u^{\ast }$。

• 目标函数：$J_{\Sigma }={\sum }_{k=1}^3{J}_k,J_k=\frac{1}{T}{\int }_0^T{j}_k(t{)}^{2}dt$
  这个目标函数描述的是：首先，将三维的运动的任务分解为单独一个维度再一起考虑，然后每一个维度考虑的是一段时间T内jerk的平均变化程度，这里平方是因为jerk自身表示加速度的导数，有正有负。
• 状态：$s_k=\left(p_k,v_k,a_k\right)$，状态某一个维度上的位置、速度以及加速度
• 输入：$u_k=j_k$，输入为加速度的导数jerk
• 系统方程：$\dot{s}=f_s(s,u)=(v,a,j)$

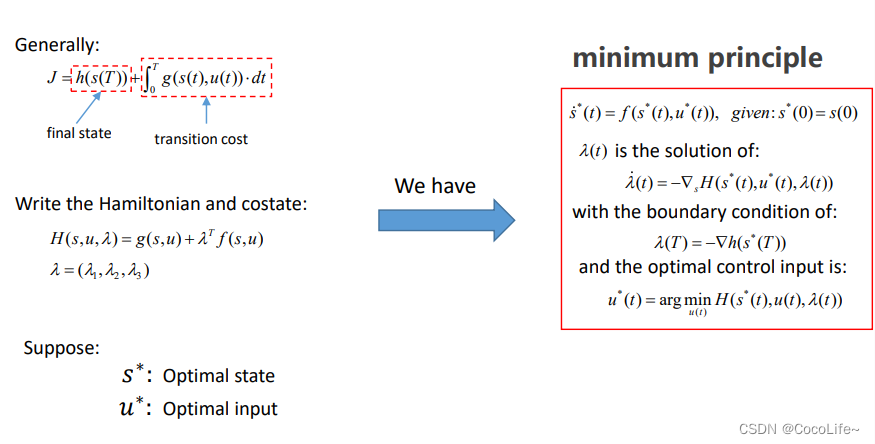
这里以庞特里亚金极小值定理为例展现整个计算的过程，

1. 首先根据系统方程中变量的个数，需要定义协态$\lambda =\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$
2. 而后构造汉密尔顿函数
   $\begin{array}{rl}H(s,u,\lambda )& =\frac{1}{T}{j}^2+{\lambda }^T{f}_s(s,u)\\ & =\frac{1}{T}{j}^2+{\lambda }_{1}v+{\lambda }_{2}a+{\lambda }_{3}j\end{array}$
3. 极小值定理做的事情，就是协变量$\lambda$是如下方程的解：
   $\dot{\lambda }(t)=-{\nabla }_{s}H\left(s^{\ast }(t),u^{\ast }(t),\lambda (t)\right)$
   即汉密尔顿函数在状态与输入都是最优的情况下对状态求的偏导数。公式表示 $\lambda (t)$ 的时间导数等于汉密尔顿函数在最优状态、最优控制和当前伴随变量下对状态的梯度的相反数。边界条件：$\lambda (T)=-\nabla h\left(s^{\ast }(T)\right)$，表示控制最后的时刻对末状态的惩罚。
   通过这种方式最优控制量：$u^{\ast }(t)=\arg {\min }_{u(t)}H\left(s^{\ast }(t),u(t),\lambda (t)\right)$，即在找到最优的$s^{\ast }$，后怎么找到最优的输入$u^{\ast }$，使得汉密尔顿函数最小。
4. 根据$\dot{\lambda }(t)=-{\nabla }_{s}H\left(s^{\ast }(t),u^{\ast }(t),\lambda (t)\right)$与本例中的汉密尔顿函数：
   可以求出$\dot{\lambda }=-{\nabla }_{s}H\left(s^{\ast },u,\lambda \right)=\left(0,-{\lambda }_1,-{\lambda }_2\right)$，即汉密尔顿函数对位置、速度、加速度的偏导数，再加个负号。
5. 根据$\dot{\lambda }$，求出$\lambda$的一组解，
   $\lambda (t)=\frac{1}{T}\left[\begin{array}{c}-2\alpha \\ 2\alpha t+2\beta \\ -\alpha t^2-2\beta t-2\gamma \end{array}\right]$，因为本例中没有施加终末状态的软约束，是强制的必须让系统达到最后的状态，所以这个求解所需的边界条件即是我们规定的最后的状态。
6. 现在我们利用得到的$\lambda$去计算最优控制量，$\begin{array}{rl}{u}^{\ast }(t)& =j^{\ast }(t)=\arg \underset{j(t)}{\min }H\left(s^{\ast }(t),j(t),\lambda (t)\right)\\ & =\frac{1}{2}\alpha t^2+\beta t+\gamma \end{array}$
   这里就是把协态的那一组解，带入汉密尔顿函数，然后对jerk做偏导，得到极值点对应的j的值。需要注意的是，由于s已经取到optimal了，其中的v和a其实也已经固定了，所以求偏导的时候不需要管他们了。
7. jerk得到最优了之后，其实最优的s就可以得到了，因为p，v，a其实就是jerk一次次向上的积分。再加上初始的边界条件$s(0)=\left(p_0,v_0,a_0\right)$，即可得到状态的最优解：
   $s^{\ast }(t)=\left[\begin{array}{c}\frac{\alpha }{120}{t}^5+\frac{\beta }{24}{t}^4+\frac{\gamma }{6}{t}^3+\frac{a_0}{2}{t}^2+v_{0}t+p_0\\ \frac{\alpha }{24}{t}^4+\frac{\beta }{6}{t}^3+\frac{\gamma }{2}{t}^2+a_{0}t+v_0\\ \frac{\alpha }{6}{t}^3+\frac{\beta }{2}{t}^2+\gamma t+a_0\end{array}\right]$
   当然，这里面的系数还没有定，这时候就要用到终点的边界条件$s_f$去确认了。
   整理之后，
   $\left[\begin{array}{lll}\frac{1}{120}{T}^5& \frac{1}{24}{T}^4& \frac{1}{6}{T}^3\\ \frac{1}{24}{T}^4& \frac{1}{6}{T}^3& \frac{1}{2}{T}^2\\ \frac{1}{6}{T}^3& \frac{1}{2}{T}^2& T\end{array}\right]\left[\begin{array}{l}\alpha \\ \beta \\ \gamma \end{array}\right]=\left[\begin{array}{c}\Delta p\\ \Delta v\\ \Delta a\end{array}\right]$
   其中，$\left[\begin{array}{c}\Delta p\\ \Delta v\\ \Delta a\end{array}\right]=\left[\begin{array}{c}{p}_f-p_0-v_{0}T-\frac{1}{2}{a}_0{T}^2\\ v_f-v_0-a_{0}T\\ a_f-a_0\end{array}\right]$，
   最后即可解得，$\left[\begin{array}{l}\alpha \\ \beta \\ \gamma \end{array}\right]=\frac{1}{T^5}\left[\begin{array}{ccc}720& -360T& 60T^2\\ -360T& 168T^2& -24T^3\\ 60T^2& -24T^3& 3T^4\end{array}\right]\left[\begin{array}{c}\Delta p\\ \Delta v\\ \Delta a\end{array}\right]$。
   带入计算目标函数$J$：$J={\gamma }^2+\beta \gamma T+\frac{1}{3}{\beta }^2{T}^2+\frac{1}{3}\alpha \gamma T^2+\frac{1}{4}\alpha \beta T^3+\frac{1}{20}{\alpha }^2{T}^4$，最后得到的结果应该只跟$T$相关了，通过求$J$的极值也可以求出最优的$T$。
   终点边界条件可以完全fix也可以部分fix：
   

启发式设计

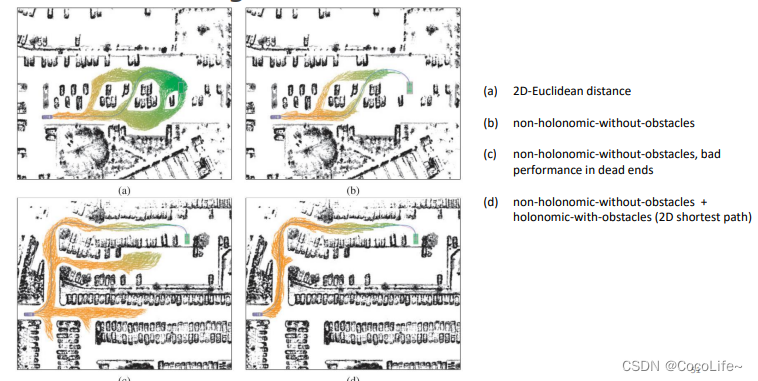
从状态空间采样搜索路径的方法不具备启发式函数，也就是漫无目的的去搜索。结合之前几个章节的启发式函数的内容，在这里同样可以引入heuristic。
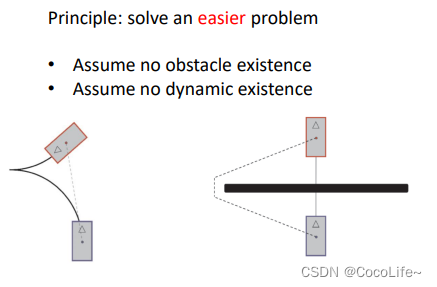
当然在这里有两种假设:

• 假设没有障碍物存在
• 假设没有动力学存在
  

Hybrid A*

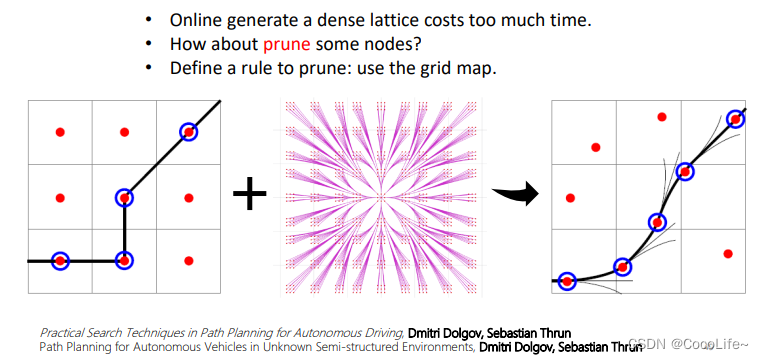
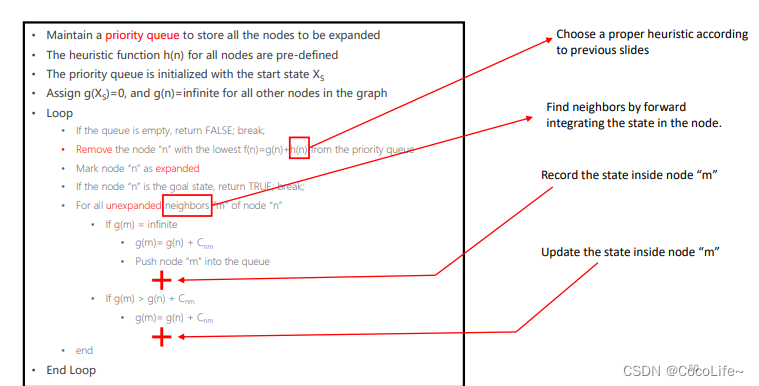
思路：A* + lattice graph，对比较稠密的图进行剪枝（栅格地图每一个格子里只要一个状态），跟A*的思路一样，区别就是邻居节点的选择是选择相邻的一些邻状态点，然后启发式函数的选择有一些区别。

Kinodynamic RRT*

上面介绍了基于搜索的算法，接下来介绍一个基于采样的运动学约束的path finding方法


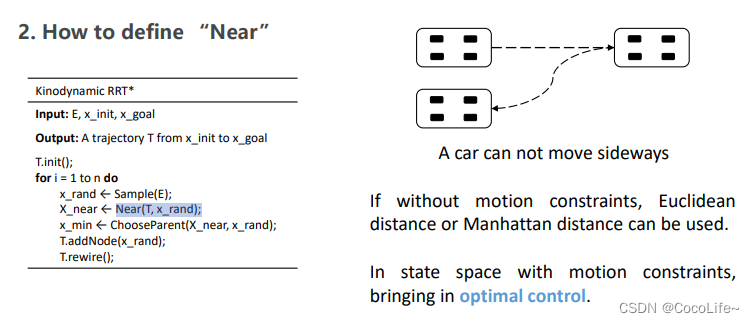
其实思路差不多，就是在采样点之间生成路径的时候不是直连了，而是通过初始状态解出运动学约束的路径，当然他这里的求解方式跟上面讲的利用汉密尔顿函数的不太一样，这里不去细说了。

RRT*用球形的范围找周围采样点，那个时候的cost就是距离，那这里图里面的点都是不同的状态点，cost是很复杂的一个高维的公式，那就需要在当前状态找到cost在给定范围内的节点（很多个高维的椭球），找利用cost在给定范围r找父节点的集合就是前向可达集，同理有后向可达集。

本文仅作个人笔记之用，如有纰漏，欢迎大家指正和讨论！希望可以和大家一起进步nie！