开源代码分享(30)-肺部性能优化算法(Lungs performance-based optimization, LPO)

参考文献

[1] Ghasemi M, Zare M, Zahedi A, et al. Optimization based on performance of lungs in body: Lungs performance-based optimization (LPO)[J]. Computer Methods in Applied Mechanics and Engineering, 2024, 419: 116582.

1.算法简介

        本文介绍了基于肺功能的优化算法（LPO），这是一种新颖高效的算法，灵感来源于人体肺部智能高效的表现。LPO从呼吸系统复杂的机制和可适应性中汲取灵感。肺部在氧气交换方面表现出卓越的效率，展示了其在功能优化方面的高水平。强制振荡技术测量空气压力和气流速率，评估呼吸系统作为电阻抗。阻抗曲线有两个明显的组成部分，呼吸系统阻力（ZR）和呼吸系统反抗（ZX），这可以从临床和工程角度来分析，以深入了解呼吸系统的运作方式。LPO旨在通过模拟和利用这种自然效率，提供解决复杂优化问题的创新方法。为了评估LPO的有效性，研究人员使用CEC2005和CEC2014无约束优化函数以及工程设计优化问题进行了实验。这些问题与文献中提出的众多现代算法进行了比较。结果表明，LPO在处理这些优化问题上表现出色，并展示了处理各种现代优化挑战的潜力。研究结果突显了LPO作为一种新型优化算法的强大和有效性。凭借其灵感源自肺部复杂功能的特点，LPO在优化领域提供了独特的视角。它处理各种优化问题的能力以及在各个领域应用的潜力使得LPO成为未来研究和实际应用中一个具有前景的算法。

2.算法原理

2.1 算法灵感来源

        LPO的灵感来自于体内肺部的表现。这部分研究将定义所提出的元启发式优化方法的许多部分，该方法是基于人体中规则和有目的的功能的数学建模。

        肺是人体内的一个关键器官，负责从周围空气中过滤氧气，并将其有效地输送到循环系统中。此外，它还负责在气体交换过程中从循环系统中去除二氧化碳，并将其排放到空气中。

        呼吸系统可以用电子模型进行建模，评估肺功能的最常用方法是强迫振荡技术。该技术涉及测量呼吸系统入口处的空气压力和气流速率，从而可以计算其电阻抗。从脉冲振荡系统（IOS）测量中得出的阻抗曲线由复阻抗的实部（呼吸阻力ZR）和虚部（呼吸电抗ZX）组成，这些可以从临床和工程角度进行分析。这些阻抗曲线可以与由电子元件组成的模型相关联，这些电子元件模拟了呼吸系统固有的阻力、顺应性和惯性。通过扩散穿过组织片的气体体积遵循菲克定律[82]：

式中，ΔP → 是压力梯度，A 是横截面积，d 是片材的厚度，K 是气体扩散系数。已经为呼吸系统和肺的功能引入了许多模型 ，肺功能被建模为图 1 中的简单 RC 电路。值得注意的是，我们在这里做了一些简化。压力变化可以表示如下：

第i个粒子（Xi）将根据其将要获得的位置在血管中移动。另一方面，在优化领域，它可以向更优化的位置移动或停留在其当前位置。LPO的数学建模和灵感已经在表1中进行了描述。

表1 LPO的灵感

肺中的元素或功能	LPO算法中的等价概念
空气和血液质量	成员运动（成员在问题范围内的运动）
空气中的二氧化碳分离及血液在静脉中的流动	问题范围内的成员运动
肺部的更佳性能	目标函数
呼吸和呼出	生成
血液中的二氧化碳分离	群体组成与交叉
电路理论中的建模	在LPO算法中建模
f(x)	f(x)
C	f(x)×0.5×sin(θ)
Iter	迭代次数
fr	频率（可能指振荡频率或其他与频率相关的参数）
Value	值
Position	位置

2.2 算法基本原理

        LPO是一种优化算法，它从一个初始群体或空气质团开始，标记为Mi，其中i=1,2,…, Npop，这些质团进入身体的功能循环中的血液，并创建新的群体。这个初始群体是在目标问题范围的两个最大值（Mmax）和最小值（Mmin）之间随机生成的。这个初始群体起到了和血液中的气体质团或粒子相同的作用。

1）空气进出肺部的过程

        如前所述，我们为肺部选择了RC模型，并考虑到建模参数，我们假设进入肺部的空气质团的位置如下，这在优化问题中就是初始群体的新位置。

式中，D代表问题的维度，Iter代表算法的当前迭代次数。

2） 空气中的二氧化碳分离和血液在静脉中的流动

        肺部从空气中分离出的氧气质量被输送到血液中。这个质量Mi相当于问题空间中种群的移动。进入血液的氧气的移动可以模拟为等式（12）。也就是说，血液通过施加在其上的压力进行移动。它从压力更大的一侧（即，适应度值更好的一侧）移动到压力较小的一侧（即，适应度值较弱的一侧）。

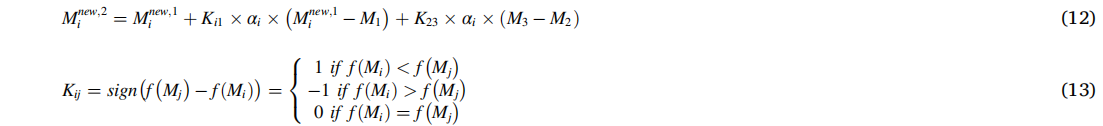
式中，Kij支配着动脉内第一块血块的运动方向，即Mi的运动方向。在每个循环周期中，αi是一个介于0到1之间的数字，它决定了移位的值，并趋向于一个优越的量。

3）从血液中分离二氧化碳

        如表1所示，我们将这一作用建模为粒子组合和交叉如下：

式中，si是一个似然值，由于肺部对血液的净化，该值随着每次呼气而减少，并且它与呼吸次数Ne（包括吸气和呼气）呈反比关系：

其中，Ne的值由用户指定。

        如前所述，每次迭代过程中会进行Ne次吸气和呼气。如果在每个阶段所需的质量有所改善，它就会取代当前位置。也就是说，如果Mnew,3_ij的位置比Mi好，那么Mi就会被替换。重要的是要注意，Mnew,3_ij在第二次吸气和呼气之后被用于等式（16）：

这个优化循环将持续设定的迭代或脉冲次数。图2总结了LPO算法使用的优化过程。

算法1. LPO的伪代码  
首先，我们向算法提供参数Ne和Npop（种群数量），以及所需的控制参数Mmin、Mmax和D。  
其次，生成初始种群，数量为Npop，并获取它们的目标函数值。  
for i = 1: Npop  
    M = Mmin + rand(1,D) × (Mmax - Mmin)  
    theta = 2 × rand  × π
    alpha = rand(1,D)
end
然后，在肺部中找到粒子的新位置，并进行Ne次的吸入和呼出。  
如果某个成员获得更好的位置，用新的解替换当前解；  
否则，该成员保持其先前位置。这表示：  
for1 i = 1: Npop  
    for2 K = 1: Ne  
        式（4）
        if K == 1  
           式(5)  
        endif 
        for3 j = 1: D  
            if sj > rand  
                式(7)  
            else  
                式(8)  
            endif  
        end(for3)  
        if f(Mnew,3) < f(Mi)  
            式（9）  
        endif  
        式(10)
        式(11)
    end(for2)  
end(for1) 
执行以上步骤直到用户希望的迭代次数或算法达到用户可接受的最优解。  
然后，在输出中打印解决方案。这个循环将持续进行，直到执行了所需次数的迭代或算法达到了由用户确定的可接受的最优解。

3.运行结果分析

4.代码获取方式

        LPO的源代码可以在基于肺部性能的优化 （LPO） |优化应用 (optim-app.com) 上公开获取。