一般来说对于机械臂中存在闭链结构的,比如一些码垛机器人,进行参数辨识的时候往往在建模的时候会使用拉格朗日法进行建模,但是拉格朗日的计算效率比较低因此最好还是使用牛顿欧拉进行建模。
使用牛顿欧拉对闭链的机械臂进行运动学建模时候,需要将闭链转化为开链。
之后的辨识思路可参考->【机械臂算法】机械臂动力学参数辨识仿真。
这里使用simscape进行仿真验证。
辨识过程如下:
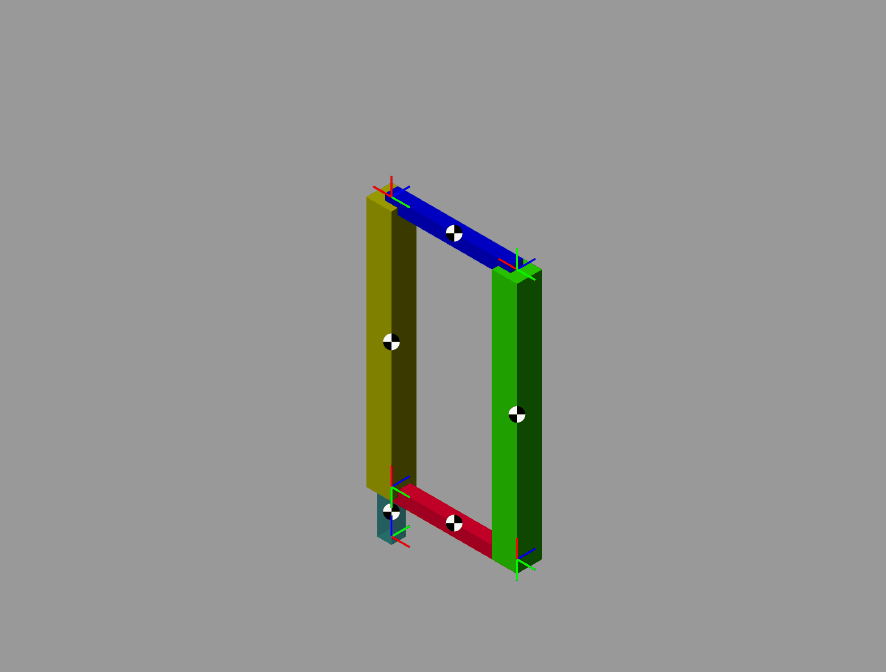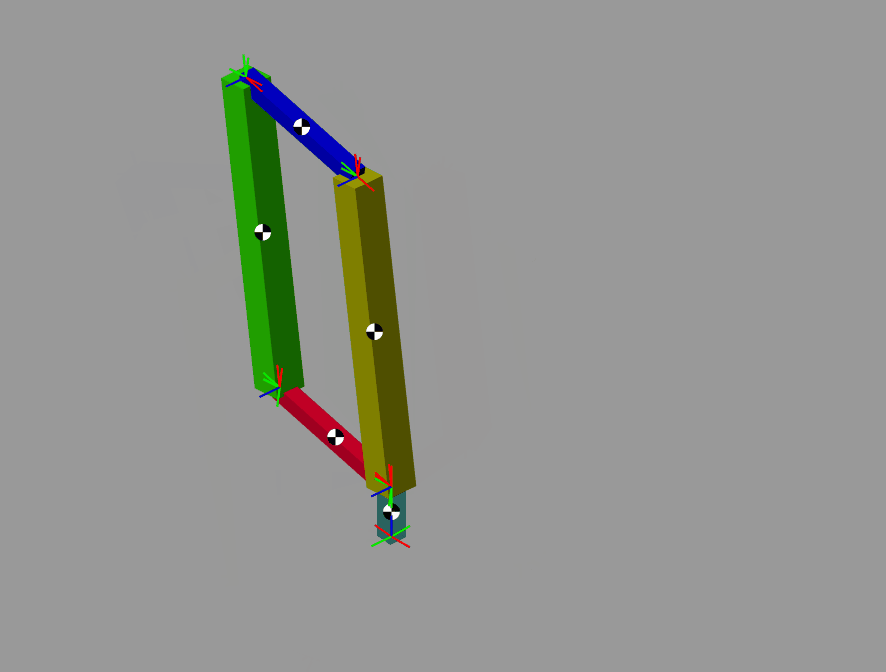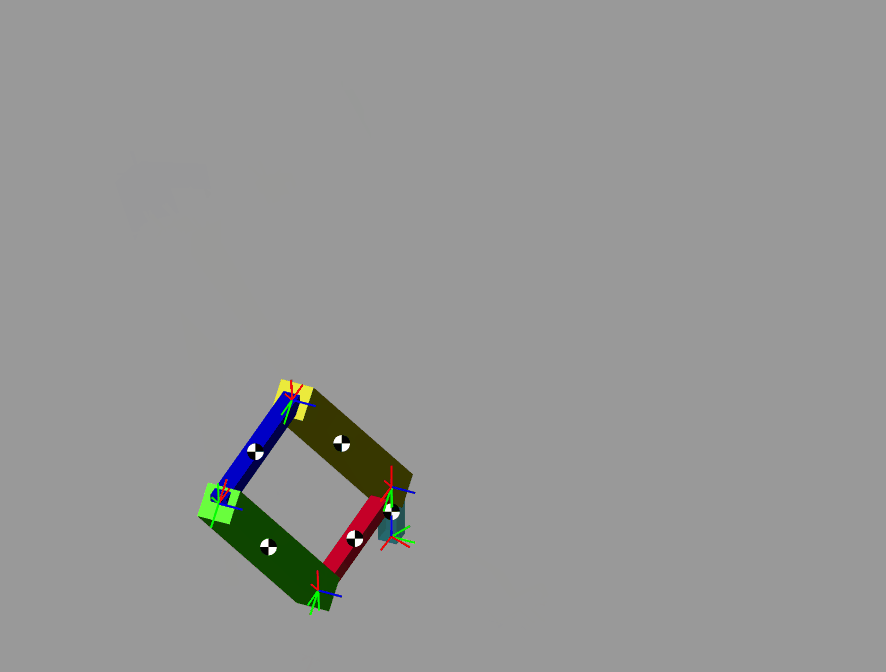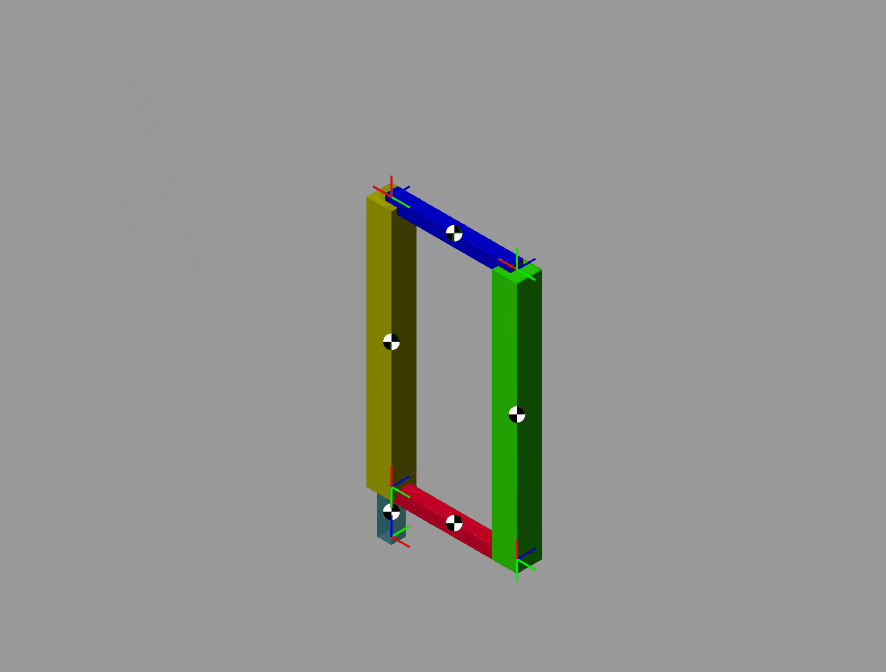
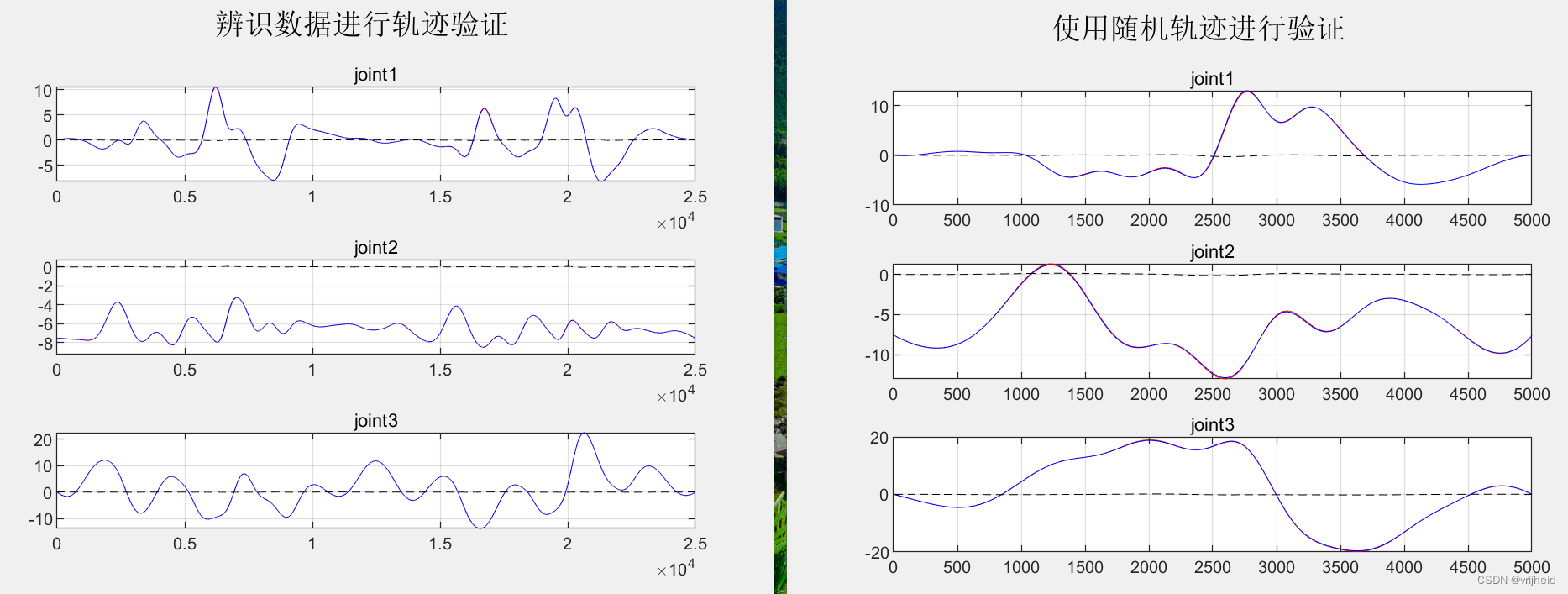
验证结果如下:
一般来说对于机械臂中存在闭链结构的,比如一些码垛机器人,进行参数辨识的时候往往在建模的时候会使用拉格朗日法进行建模,但是拉格朗日的计算效率比较低因此最好还是使用牛顿欧拉进行建模。
使用牛顿欧拉对闭链的机械臂进行运动学建模时候,需要将闭链转化为开链。
之后的辨识思路可参考->【机械臂算法】机械臂动力学参数辨识仿真。
这里使用simscape进行仿真验证。
辨识过程如下:

验证结果如下:

 4007
4007

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


