手眼标定原理

一、前言

手眼标定在很多应用场景中都是必须的，抓取场景中相机拍摄到的物品，怎么让机械臂能抓的到，这里边就需要用到手眼标定。博主当前的课题需要用到手眼标定，本以为这东西发展了这么多年，随便调几个opencv函数应该手拿把掐，结果精度却不太能让人满意，所以准备沉下心来看看各个环节的原理，找一下到底是哪里出了问题。

二、手眼标定基本流程

根据相机安装位置的不同，手眼标定分为两大类：眼在手上和眼在手外，我只用到了眼在手上，所以本文只包含此部分内容。
需要的前置知识：机器人学（懂个刚体变换就ok了），线性代数。

a. 符号定义

为了方便之后的阅读，本文符号与Tsai的论文[1]大致统一。
$G_i$: 第$i$个拍照点，末端夹爪（gripper）的坐标系
$C_i$: 第$i$个拍照点，相机（camera）的坐标系
$T$: 标定物（calibration target）坐标系，这个坐标系是任意建立的，通常会令坐标系的的$x、y$平面与标定板平面重合
$B$: 机器人基座（base）坐标系
$W$: 世界（world）坐标系
$H_{cg}$: 相机坐标系到夹爪坐标系的刚体变换矩阵，也就是齐次变换矩阵（homogeneous transform matrix）
$H_{gij}$: 第$i$个拍照点到第$j$个拍照点的夹爪坐标系变换矩阵

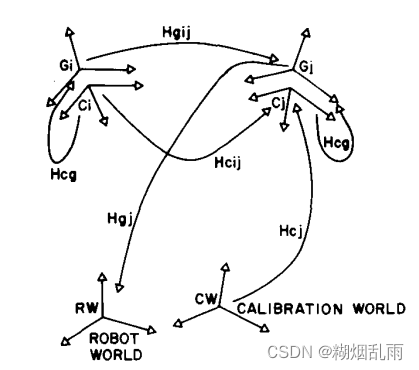
b. 核心公式

手眼标定的核心是如下公式：
$$H_{g_{ij}}{H}_{c_i{g}_i}=H_{c_j{g}_j}{H}_{c_{ij}}\text{\hspace{1em}(1)}$$
很显然，由于相机是固定在机械臂末端的，所以$H_{c_i{g}_i}=H_{c_j{g}_j}$，可得
$$H_{g_{ij}}{H}_{cg}=H_{cg}{H}_{c_{ij}}\text{\hspace{1em}(2)}$$
这个公式描述了$H_{c_i{g}_j}$的两种不同获取方式

• $H_{g_{ij}}=H_{g_{j}b}^{-1}{H}_{g_{i}b}$，$H_{gb}$是末端相对于基座的相对位姿，正常的机械臂都有读取$H_{gb}$的功能，唯一的差异是读出来的可能是$XYZRPY$，需要自己确定机械臂欧拉角顺序（这个顺序非常重要），然后转换成$H_{gb}$。
• $H_{c_{ij}}=H_{c_{j}t}^{-1}{H}_{c_{i}t}$，$H_{ct}$是相机相对于标定板的相对位姿，可以通过标定相机外参来获得

c. 数学建模

观察公式（2），未知量只有$H_{cg}$，所以（2）式其实是一个$AX=XB$形式的矩阵方程。这个东西在数学上其实有明确的定义，被称为齐次西尔维斯特方程（Homogeneous Sylvester Equation），可以转换成线性方程的形式$QY=0$。但很显然这个方程求解很复杂，使用经典的Bartels–Stewart算法去求解一般的西尔维斯特方程的复杂度未$O(n^3)$，$n$为$A$矩阵的大小。并且$H_{cg}$矩阵是齐次变换矩阵，形式特殊
$$H_{cg}=\left[\begin{array}{cc}{R}_{cg}& T_{cg}\\ 0& 1\end{array}\right]$$
相当于引入了新的约束，所以在手眼标定场景下，这个方程有新的解法，我这里采用的是一种非常经典的算法——Tsai法。

三、Tsai法论文阅读

本章分为四个部分，第一部分是对使用到的定义进行说明，第二部分先列出Tsai法的基本步骤，第三部分对必要公式进行推导，第四部分是对误差的分析。这里仅作个人笔记整理，一些基本数学知识尽量补充，如有需要可以去看论文原文，里边写的非常详细。

a. 前置知识与定义

1. 欧拉旋转定理

这个非常关键，百度可得：

在三维空间里，假设一个刚体在做一个旋转的时候，刚体内部至少有一点固定不动，则此位移等价于一个绕着包含那固定点的固定轴的旋转。

他讲了这样一件事情，不管刚体绕着多少个轴旋转多少次多少角度，最后总能找到一个轴和一个绕这个轴旋转的角度，来描述整个旋转过程。

2. 向量的反对称矩阵形式

$$n=[n_1,n_2,n_3{]}^T$$
$$skew(n)=\left[\begin{array}{ccc}0& -n_3& n_2\\ n_3& 0& -n_1\\ -n_2& n_1& 0\end{array}\right]\text{\hspace{1em}(3)}$$
这个东西通常用来描述叉乘
$$n\times v=skew(n)\cdot v$$

3. Rodrigues公式

上面提到的轴角形式虽然直观，但是它不方便计算，而Rodrigues公式的作用就是将轴角形式的旋转转换为旋转矩阵，公式如下：
$$R=I+\sin \theta skew(n)+(1-\cos \theta )skew(n{)}^2\text{\hspace{1em}(4)}$$
其中$n$为旋转轴，$\theta$为绕$n$轴旋转的角度。值得注意的是，因为旋转轴咋转都还是旋转轴，所以$R\cdot n=n$，也就是说$n$其实是$R$的一个特征向量，对应的特征值为1。

Tsai法中使用了一个修改版本的Rodrigues公式，它首先将$n$和$\theta$合到一起，令$$P_r=2\sin \frac{\theta }{2}{n}^T$$将这个式子带入到（4）式中，可以获得一个新形式的Rodrigues公式，对应论文里的（10），文中说它可以消除掉三角函数，可能是误差分析里用到了这个东西，但那部分我没有看。

4. 基本定义

上一小节中提到的$P_r$非常重要！！！！

除了这个以外文中还提到了如下定义：

有的时候定义并没有啥道理，可能在推导中的某一步会简化计算，因此作者就做出了这样的定义，可以不用太过纠结。

b. 基本步骤

1. 计算$R_{cg}$

1. 计算$P_{cg}^{\prime }$

求解以下线性方程组
$$skew(P_{g_{ij}}+P_{c_{ij}})P_{cg}^{\prime }=P_{c_{ij}}-P_{g_{ij}}\text{\hspace{1em}(5)}$$
注意：

2. 计算${\theta }_{R_{cg}}$

$${\theta }_{R_{cg}}=2{\tan }^{-1}|P_{cg}^{\prime }|$$

3. 计算$P_{cg}$

$$P_{cg}=\frac{2P_{cg}^{\prime }}{\sqrt{1+|P_{cg}^{\prime }{|}^2}}$$

2. 计算$T_{cg}$

求解以下线性方程组
$$(R_{g_{ij}}-I)T_{c}g=R_{cg}{T}_{c_{ij}}-T_{g_{ij}}$$

c. 原理推导

论文中给出了一系列引理，但证明给的比较简略。

step1

1. $R_{g_{ij}}=R_{cg}{R}_{c_{ij}}{R}_{cg}^T$
   证明：将（2）展开可以得到这个结果
   $$\left(\begin{array}{cc}{R}_{g_{ij}}& T_{g_{ij}}\\ 0& 1\end{array}\right)\left(\begin{array}{cc}{R}_{cg}& T_{cg}\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}{R}_{cg}& T_{cg}\\ 0& 1\end{array}\right)\left(\begin{array}{cc}{R}_{c_{ij}}& T_{c_{ij}}\\ 0& 1\end{array}\right)$$
   $$\therefore \left(\begin{array}{cc}{R}_{gij}{R}_{cg}& R_{g_{ij}}{T}_{cg}+T_{g_{ij}}\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}{R}_{cg}{R}_{cij}& R_{cg}{T}_{c_{ij}}+T_{cg}\\ 0& 1\end{array}\right)\text{\hspace{1em}(6)}$$
   $$\begin{gathered} \therefore R_{g_{ij}}{R}_{cg}=R_{cg}{R}_{c_{ij}}\because R_{cg}^{-1}=R_{cg}^T \\ \therefore R_{g_{ij}}=R_{cg}{R}_{c_{ij}}{R}_{cg}^T\text{\hspace{1em}(7)} \end{gathered}$$
   可知$R_{g_{ij}}和R_{c_{ij}}$相似

2. $P_{g_{ij}}=R_{cg}{P}_{c_{ij}}$
   证明：
   $$\because R_{g_{ij}}{P}_{g_{ij}}=P_{g_{ij}}{R}_{c_{ij}}{P}_{c_{ij}}=P_{c_{ij}}$$
   将（7）代入可得：
   $$R_{cg}{R}_{c_{ij}}{R}_{cg}^T{P}_{g_{ij}}=P_{g_{ij}}$$
   $$\therefore R_{c_{ij}}{R}_{cg}^T{P}_{g_{ij}}=R_{cg}^T{P}_{g_{ij}}\text{\hspace{1em}(8)}$$
   $$\therefore R_{cg}^T{P}_{g_{ij}}=P_{c_{ij}}\therefore P_{g_{ij}}=R_{cg}{P}_{c_{ij}}\text{\hspace{1em}(9)}$$

看到（8）式，可以说明$R_{cg}^T{P}_{g_{ij}}$也是$R_{c_{ij}}$特征值为1时的特征向量，一开始没有想明白，觉得$R_{cg}^T{P}_{g_{ij}}和P_{c_{ij}}$应该差一个倍数，但实际上$R_{cg}$里包含了$R_{c_{ij}}和R_{g_{ij}}$特征向量的信息，如果缩放特征向量，$R_{cg}$就会发生改变。

这里还能获得另一个结论，${\theta }_{R_{g_{ij}}}={\theta }_{R_{c_{ij}}}$

3. $P_{cg}\perp (P_{g_{ij}}-P_{c_{ij}})$
   由引理2可以得知，$P_{g_{ij}}$是由$P_{c_{ij}}$绕$P_{cg}$旋转得到得，旋转不会改变模长，所以几何表示如下：
   
   几何证明非常直观，除此以外论文中还给出了一种代数证明方法。
   有了这个引理，我们可以获得一个结论，$P_{cg}$一定位于垂直于面$O{C}_{ij}{G}_{ij}$（对应于上图得$OCG$），并且经过$C_{ij}{G}_{ij}$的中点。那么再设置一个拍照点，我们就可以再获得一个这样的平面，这样两个平面的交线即为$P_{cg}$。但这种方法对噪声非常敏感，所以文中没有用这种方法。

进一步，我们可以得知，如果想求解$P_{cg}$至少要三个拍照点，形成两对变换。

4. $(P_{g_{ij}}+P_{c_{ij}})\times P_{cg}与P_{g_{ij}}-P_{c_{ij}}共线$
   这个用上边的图很容易就可以解释，自己可以想一下。
   但是共线还不够，左右两边还相差一个倍数。回看一下之前对于$P_{cg}^{\prime }$的定义，有一个很奇怪的系数，在这就起了作用，带入之后可以发现
   $$|(P_{g_{ij}}+P_{c_{ij}})\times P_{cg}^{\prime }|=|P_{g_{ij}}-P_{c_{ij}}|$$
   $$\therefore (P_{g_{ij}}+P_{c_{ij}})\times P_{cg}^{\prime }=P_{g_{ij}}-P_{c_{ij}}$$
   $$\therefore skew(P_{g_{ij}}+P_{c_{ij}})P_{cg}^{\prime }=P_{g_{ij}}-P_{c_{ij}}\text{\hspace{1em}(10)}$$
   至此完成了对step1的证明

step2

$$P_{cg}^{\prime }=\frac{1}{2\cos (\frac{{\theta }_{R_{cg}}}{2})}{P}_{cg}$$
$$P_{cg}=2\sin \frac{\theta }{2}{n}^T$$
$$\therefore P_{cg}^{\prime }=\frac{\sin (\frac{{\theta }_{R_{cg}}}{2})}{\cos (\frac{{\theta }_{R_{cg}}}{2})}{n}^T\therefore |P_{cg}^{\prime }|=\tan (\frac{{\theta }_{R_{cg}}}{2})$$
$$\therefore {\theta }_{R_{cg}}=2{\tan }^{-1}|P_{cg}^{\prime }|$$

step3

$$P_{cg}^{\prime }=\frac{1}{2\cos (\frac{{\theta }_{R_{cg}}}{2})}{P}_{cg}$$
带进去算就行了

step4

根据（4），因为右上角元素相等，所以$$R_{cg}{T}_{c_{ij}}+T_{cg}=R_{g_{ij}}{T}_{cg}+T_{g_{ij}}$$
$$\therefore (R_{g_{ij}}-I)T_{cg}=R_{cg}{T}_{c_{ij}}-T_{g_{ij}}\text{\hspace{1em}(11)}$$

线性方程组解的情况分析

跳出推导，想要使用Tsai法求解手眼标定，最重要的就是求解（10）（11）两个线性方程组。

1. $skew(P_{g_{ij}}+P_{c_{ij}})P_{cg}^{\prime }=P_{g_{ij}}-P_{c_{ij}}$

$skew(P_{g_{ij}}+P_{c_{ij}})$的秩为2，而$P_{cg}^{\prime }$有三个自由度（$P_{cg}^{\prime }$不一定是单位向量），所以再次证明至少需要三个拍照点，才能求解这个方程。

并且要求

2. $(R_{g_{ij}}-I)T_{cg}=R_{cg}{T}_{c_{ij}}-T_{g_{ij}}$

$(R_{g_{ij}}-I)$的秩为2，而$T_{cg}$作为平移向量有三个自由度，仍说明需要三个拍照点，组成两对齐次变换才能完成Tsai求解。

并且要求

可以看出至少要有两组不共线的$P_{g_{ij}}$才能求解这两个方程，因此设置拍照点的时候需要注意这个事情，并且我们可以推出SCARA机器人是没有办法用这个方法做手眼标定的。

d. 误差

论文中一顿证明（实在看不下去），得到了如下式子

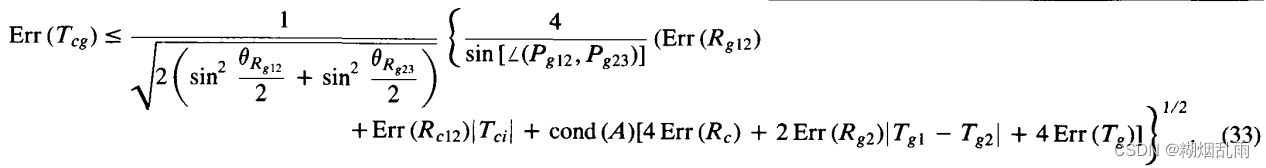
1. 提升精度的方法

论文中给出了如下几点：

1. 从$i$拍照点变换到$j$拍照点旋转的角度尽可能大
2. $H_{g_{ij}}$和$H_{g_{jk}}$二者旋转轴的角度要尽可能大
3. 最小化相机镜头和标定板的距离，这需要一个小尺寸的标定板以及合适的可以用于近距离观测的镜头
4. 最小化末端坐标系原点在不同拍照点时的距离
5. 使用尽可能多的拍照点，因为计算速度很快，所以多选择几个拍照点也不是什么问题，文中说“The error due to nonsystematic sources will be reduced by a factor of $\sqrt{N}$, where N is the number of stations”
6. 高精度的相机标定算法可以有效提升精度
7. 标定前也要对机器人本体进行标定

论文中给出了一种拍照位姿设置范例

2. 论文中提到的误差参考值

本文所用实验平台为480 $\times$ 388的相机，repeatability for linear joint is 4 mil， and that for the rotary joints 1 mard的七自由度机械臂，标定板是一个背光玻璃板，上边是用photographic emulsion打印的disc（这个我不知道是圆点还是同心圆，论文中的图都看不清）。

由于不存在真值，所以本文通过如下方式评估误差

• 移动机械臂到$2N$个不同拍照点，对于每个拍照点，计算相机外参$H_{c_i}$，记录机械臂相对于基座的相对位姿$H_{g_i}$。
• 使用$1$~$N$号拍照点计算$H_{cg}$
• 对于每一个拍照点计算$H_{RC}$，这个是基座到标定板的相对位姿，$H_{RC}=H_{c_i}^{-1}{H}_{cg}^{-1}{H}_{g_i}^{-1}$，并将这$N$次的结果求平均。
• $N$~$2N$的拍照点被称为验证点，对于每个验证点，预测相机到基座的齐次变换$H_{cg}^{-1}{H}_{gk}^{-1}$，与$H_{ck}{H}_{RC}$做比较。

需要注意，这种评估方式得到的误差包含外参标定误差以及机械臂定位误差，文中指出$T_{cg}$的误差为$10.66mil=0.271mm$，旋转误差大约是$2.88mrad$（这地方我建议再回去读下论文，我其实没太看懂文中这个部分）

3. 结论

这篇论文介绍了一个高速的、高准确度的、用途广泛的、简单的、全自动的手眼标定方法。在论文发表时刻是最快最准的算法（现在不知道发展到了什么水平）。作者指出了一个需要频繁需要手眼标定的场景，机械臂去抓相机拍照，拍完再把相机放回原位，哈哈哈哈，想的这个应用场景有点搞笑。

参考文献

[1]Tsai R Y, Lenz R K. A new technique for fully autonomous and efficient 3 d robotics hand/eye calibration[J]. IEEE Transactions on robotics and automation, 1989, 5(3): 345-358.