样本量估算超实用说明

样本量估算是一个老生常谈的话题，也是让不少临床医生头疼的话题。很多情况下，可能统计学家都会奇怪：样本量估算是挺简单的，照着公式代入相应的参数就行了，为什么好多人还是不大清楚呢？

我也考虑过这个问题，后来我想，可能最主要的问题不在于样本量估算本身是不是简单，而是与样本量估算的一系列问题。如果只说样本量估算公式本身，确实非常简单，就算没有统计软件，用excel自己算算都很容易，更不用提有这么多的便捷的统计软件了。那为什么临床医生还是每次碰到样本量问题就要去咨询统计学家呢？

我仔细琢磨了一下这个问题，决定还是再写一篇关于这个老生常谈的话题。本文所介绍的样本量估算，先只涉及组间比较的情况，这也是临床研究中最常见的情形。几乎所有统计软件都能实现组间比较的样本量估算。

我想，对于临床医生来说，大家并不是觉得样本量估算公式很麻烦，也不是不会使用统计软件，事实上，很多统计软件都无需编程，就是简单在界面中输入两三个参数值，就出来结果了。然而最大的问题不在于输入这几个数值，而是临床医生不知道这几个数值到底是什么，代表什么意思，为什么要输入这些，等等。

先说一些样本量估算前的专业设定：

第一，要先确定你的主要评价指标是什么（这是临床专业问题，如果你连这个都确定不了，那也不用做研究了），样本量是基于主要评价指标估算出来的。经常看到有的标书中写的主要评价指标是有效率，而前面的样本量估算却写着“根据两组VAS评分，计算……”。样本量估算所用到的指标，要跟你的主要评价指标一致。

第二，要确定你的主要评价指标有几个。这一点已经被强调过无数次：主要评价指标最好就是1个，不要那么多。但是，很多临床医师依然始终不愿意接受这一观点，最主要的问题就是觉得做一次研究不容易，收一次患者不容易，一定要多设置几个指标。然而，科研不会考虑你收研究对象容不容易，甚至说，评审人也不会考虑你这种现实问题，更重要的是考虑科学性。

如果从临床角度，确实需要设置2个主要评价指标，这种情况下就需要对两个指标分别估算样本量，而且估算时的一类错误需要重新分配（本文后面会有介绍）。但是仍然建议，如无必须，尽量一个主要指标就行。

当你确定了主要指标后，就可以开始估算样本量了。那估算样本量需要考虑哪些因素呢？下面从最实用的角度来说一下。

以专业的样本量估算软件PASS的界面为例（其它软件所需的参数都一样，只是界面不同而已），对于组间比较，需要指定的一共就这么几个参数（这一界面是两组均值比较）：alternative hypothesis（备择假设，更明确地说是指定单侧检验还是双侧检验）、power（把握度）、alpha（一类错误）、group allocation（两组例数比）、u1和u2（两组均值）、σ（合并标准差）。

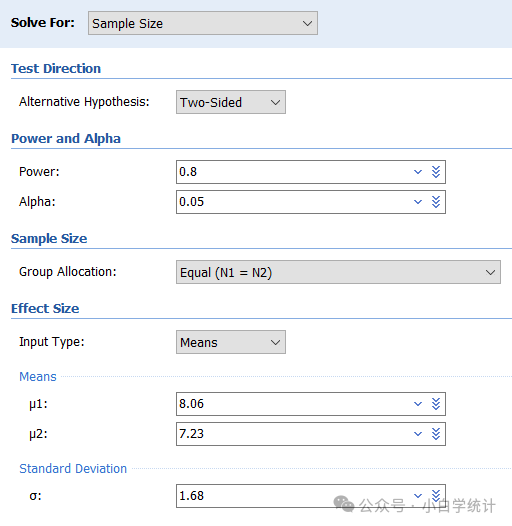
对于临床医师来说，可能有两个问题：第一，不知道该什么设定，如把握度和一类错误；第二，不知道该如何获取，如两组均值和标准差。一旦知道了，直接填上就行了。所以主要就这两个方面说一下。

第一，不知道该如何设定的内容

这部分内容是通用部分，不管是两组比较还是多组比较，不管是比较均值还是率，都需要设定这些。

单双侧、一类错误、把握度、两组例数比，需要自己设定，该如何设定呢？如果你没有任何概念，那就设定一类错误0.05，把握度0.8，这是最常用的设置。

如果你有一定的想法，比如不差钱，不差研究对象，这种情况下，可以设定提高把握度，这样可以有更大的把握能够在最后的统计学检验时出现“有统计学差异”的阳性结果。

如果你前面确定了2个主要评价指标，这时候不仅要对两个指标分别估算，而且还得重新设定一类错误。通常最简单的方式是每个指标分别指定一类错误为0.025（合起来是0.05）。其实样本量估算与后期的统计分析是相呼应的，如果你最后打算比较两个主要指标，那最后统计分析也需要按每个指标0.025来做检验，保证2个指标的一类错误合起来不超过0.05，所以事前的样本量估算也按这个来。

绝大多数情况下，统计学检验采取的都是双侧检验。但是在一些特殊场景下，建议用单侧。比如阳性治疗与安慰剂的对比、A+B与A的对比（例如，中药+西药与单独西药相比），通常这些可以设为单侧。因为如果阳性药连安慰剂都没有把握超过的话，那干脆别生产了。如果在西药的基础上增加中药，还没有把握超过单独西药的话（既增加患者的费用、又多吃了药），那这种研究意义也不大。所以在类似这些情况下，建议用单侧。

至于两组的例数比例，如无特殊情况，尽量按1:1，这是最常见的方式。有时候如果从实际角度觉得某一组的研究对象更难获得，也可以按1:2这些来，根据实际情况而定。但是，同样的例数下，1:1的效率最高。如果按1:2甚至1:3等，要达到同样的检验效果，需要比1:1的总例数多。

第二，不知道该如何获取的内容

这部分是特定部分，根据主要指标的类型而不同，如上图中给出的两组均值比较，所以需要确定的是两组的均值和标准差。如果是两组率的比较，那就需要确定两组的率。简单来说就是，比较均值，那就需要获得各组的均值和标准差；比较率，那就需要获得各组的率。

获取的方式，主要两个渠道：一是以往文献报道的结果；二是以前自己已有的结果。

有一些临床医师会一下子转不过弯来：我们本来就是要比较两组均值，那肯定是不知道这些内容，怎么还得事先就填上这些内容呢？

我想，可能多数人做的研究都不是首创，往往是想证实一些疗效等指标。这种情况下，就很可能在已有的文献中查到一些相关的内容和指标值。因为只有在大致了解所需参数的情况下，才能判断你到底需要多少样本。这就有点类似于，如果一个身高190和160的在一起，你一眼就能看出谁高谁低；而如果一个身高170和171的人在一起，你需要观察很久才能看出谁高谁低。你可以把这个观察多久想象成样本量，差别越明显，越是只需要少数例数就能发现差异；差别越小，越需要更多的例数才能发现这种差异。

可能你会说，我这个研究真的是首创，想了解一种最新的手术方式到底有没有效？试想一下，如果这真的是全新的治疗方式，你敢一下子就安排一个临床研究吗？我相信不会，至少需要在临床中先有一定的试用，逐渐发现好像效果不错，然后才准备开展一个正式的试验来证实（再更严谨点，在正式试验前，开展一个预试验）。而在这种情况下，尽管对于这个正式的试验来说是全世界首创，但是前期也已经有了一定的非正式试验的数据了，或者，预试验有了一定数据和结果，这些依然可以是作为样本量估算的参数。

所以，无论哪种情况，其实你都有可能查到相关的参数。如果以前已有类似文献报道，那就可以查文献，找找与你的研究类似的这种干预组的参数值（如两组均值、标准差）是多少。如果你是世界第一个做这种研究的，那前期你也会有一定的临床数据积累，将其作为参数值，或者就先做一个预试验，获取参数值。

另外，有的临床医师可能会说，我真的找不到跟我这个一样的两组，这怎么办？比如，你打算比较A和B两种方式，而所有的文献都没有A和B的比较，但是有的文献有A和安慰剂，有的有B和C，等等，这种情况下，那就多查一些文献，分别提取出A的参数值（均值、标准差等）和B的参数值，然后进行比较。尽管这不是最好的方式，但总比什么都没有的好。

总之，有一个依据，就比什么都没有的好。因为样本量估算本身就是一个”估算“，并不是一个十分精确的值，更多的是作为参考，有一个大致范围。如果没有任何依据，那你不知道样本量估算到底应该是50还是5000；而如果有了一个大致依据，至少你知道可能在300左右。

关于样本量的估算，其实我在以前已经写了不少，大家可以参考。不过我发现还是有很多临床医师不是很清楚到底应该怎么计算，所以本文写的再简化一些、再实际一些，希望能对临床医生有所帮助。本文并不包含所有的样本量估算内容，只是以两组比较为例，通俗说一下如何考虑，至少在使用统计软件的时候知道该如何输入参数。

另外，关于样本量我也写了几个如何使用PASS软件的文章，大家感兴趣可以看看。

更多实战课程

2022年以来，我们召集了一批富有经验的高校专业队伍，着手举行短期统计课程培训班，包括R语言、meta分析、临床预测模型、真实世界临床研究、问卷与量表分析、医学统计与SPSS、临床试验数据分析、重复测量资料分析、结构方程模型、孟德尔随机化等10门课。如果您有需求，不妨点击查看：

10门科研与统计课程介绍：含孟德尔随机化课程