【笔记】概统论与数理统计第三章知识点总结

最新推荐文章于 2023-11-01 13:14:53 发布

Dorothy30

最新推荐文章于 2023-11-01 13:14:53 发布

阅读量5k

点赞数 5

分类专栏：概统文章标签：概率论卷积统计学

本文链接：https://blog.csdn.net/weixin_44835327/article/details/118215132

版权

概统专栏收录该内容

8 篇文章

订阅专栏

3.1 二维随机变量及其分布函数

1. 二维随机变量及其分布函数

二维随机变量 (向量)：在同一个样本空间上的两个随机变量X和Y组成(X, Y)
- 由于随机变量X和Y从不同角度刻画统一随机试验，X和Y可能还存在内部联系，因此使用二维随机变量进行刻画
二维分布函数：设 (X, Y) 是二维随机向量, 对任意实数 x, y, 称

F(x, y) = P(X ≤ x, Y ≤ y)

为二维随机变量 (X, Y) 的二维分布函数（联合分布函数）

定理：设 F(x, y) 为二维随机变量 (X, Y) 的分布函数, 则
- F(x, y) 关于 x 及 y 单调不减
  - F(−∞, −∞) = F(−∞, y) = F(x, −∞) = 0, F(+∞, +∞) = 1
- F(x, y + 0) = F(x + 0, y) = F(x, y)
- 如果 x1 ≤ x2, y1 ≤ y2, 有

（矩形的区域大于0）

如果一个二元函数满足 (2),(3),(4), 那么, 他是某个二维随机变量的分布函数

2. 二维离散型随机变量及其概率分布

二维离散型随机变量：二维随机变量 (X, Y) 只取有限个或可数无穷多个点对 $(x_i, y_j),i,j=1,2,3,...$
二维概率分布/分布律（X与Y的联合概率分布）：设二维随机变量 (X, Y) 所有可能取值为 $(x_i, y_j),i,j=1,2,3,...$ ,记 ,

可用表格表示

性质
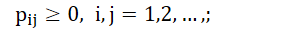
二维离散性随机变量 (X, Y) 的分布函数可以用概率分布求出

三项分布：在n重独立试验中, 若每次试验只有 A1, A2, A3 三个可能的结果, 且 0 < $p_i$ = P( $A_i$ ) < 1, i = 1, 2, 3, 则 p1 + p2 + p3 = 1。令随机变量 X1, X2分别表示 n 次试验中A1, A2 的发生次数, 则 (X1, X2) 有联合概率分布

3. 二维连续型随机变量及其密度函数

二维连续型随机变量：二维随机变量 (X, Y), 如果存在二元非负函数 f(x, y), 使得对任意实数 x, y, 有

(X, Y)：是二维连续型随机变量
f(x, y)： (X, Y) 的二维概率密度函数（ X 与 Y 的联合密度函数）

性质
- 定理：二维连续型随机变量 (X, Y) 有密度函数 f(x, y), 则
- F(x, y) 是连续函数且在 f(x, y) 的连续点 (x, y), 有
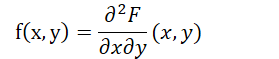
- 对平面上任意区域 G ⊂ $R^2$ , 若 f(x, y) 在 G 上可积, 有
- 对平面上任一条曲线 L, 有 P((X, Y) ∈ L) = 0
- 二维均匀分布：密度函数在随机变量的值域上是常数,令 G 是平面上一个有界区域, 若二维随机变量 (X, Y) 有密度函数
- m(G)：G 的面积
- (X, Y) ：在 G 上均匀分布，记为(X, Y) ∼ U(G)
- 描述的是点 “等可能” 地落入大小相同的子块内, 而这里大小是用面积度量的
对于Z = min(X, Y)， (Z > t) = (X > t, Y > t)
对于W = max(X, Y)，(W ≤ t) = (X ≤ t, Y ≤ t)

3.2 边缘分布及随机变量的独立性

1. 边缘分布函数及随机变量的独立性

X 及 Y 的边缘分布函数：设 F(x, y) 为二维随机变量 (X, Y) 的二维分布函数, 则 X 及 Y 的边缘分布函数 $F_X(x)$ 和 $F_Y(y)$ 有

随机变量的独立性：F(x, y) 是二维随机变量 (X, Y) 的二维分布函数， $F_X(x)$ , $F_Y(y)$ 分别为 X, Y 的边缘分布函数, 若对任意 x, y, 有

定理：设随机变量 X 和 Y 独立, g(x) 与 h(y) 分别是 x 与 y 的连续函数，那么，X1 = g(X) 和 Y1 = h(Y) 也相互独立

2. 二维离散型随机变量的边缘分布及独立性

边缘概率分布（边缘分布）：设 (X, Y) 是二维离散型随机变量，有二维概率分布

X 和 Y 都是一维离散型随机变量，有各自的分布律（边缘分布）

（X 和 Y 的分布列写在表格的边缘，所以叫做边缘分布）
随机变量 X 和 Y 独立 ⇐⇒ pij=pi⋅p⋅j，i, j = 1, 2, . . ..

3. 二维连续型随机变量的边缘分布及独立性

对二维连续型随机变量 (X, Y), 有二维密度函数 f(x, y), 则 X 和 Y 作为一维随机变量也是连续型的, 有各自的密度函数 $f_X(x), f_Y(y)$ ，相对于二维密度函数, 它们分别叫做 X 与 Y 的边缘密度函数。

定理：(X, Y) 的二维密度为 f(x, y), X 与 Y 的边缘密度分别为 $f_X(x), f_Y(y)$
X 与 Y 相互独立 ⇐⇒ f(x, y) = $f_X(x)f_Y(y)$

3.3 条件分布与条件密度

1. 条件分布函数：当P(Y=y) > 0 时，Y=y条件下X的条件分布函数为

2. 离散型随机变量的条件分布

Y = $y_j$ 条件下 X 的条件概率分布： $y_j$ 任意给定，且 P(Y = $y_j$ ) = p⋅j > 0
X = $x_i$ 条件下 Y 的条件概率分布： $x_i$ 任意给定，且 P(X = $x_i$ ) = pi⋅ > 0
性质：条件概率分布也是一个离散型概率分布
条件分布函数

3. 连续型随机变量的条件密度函数

条件分布函数：设 (X, Y) 有二维密度 f(x, y), 从而 X 与 Y 有边缘密度 $f_X(x), f_Y(y)$ , 则

条件密度函数

当边缘密度和条件密度都已知时, 我们可以求出联合密度

3.4 二维随机变量函数的分布

1. 离散型随机向量的函数的分布

当 (X, Y) 是二维离散型随机变量, 且 X 与 Y 有联合分布律 $p_ij = P(X=x_i, Y=y_j)$ ，i, j = 1, 2,...，则Z=g(X, Y)有分布律

2. 连续型随机向量的函数的分布

当 (X, Y) 为二维连续型随机变量。且有密度函数 f(x, y)。若 g(x, y) 是连续可微函数，则 Z = g(X, Y) 是一维连续型随机变量，从而有由 f(x, y) 求 Z 的密度函数的问题。方法如下：
- 确定 Z 的值域 R(Z)对任意 z ∈ R(z), 求 Z 的分布函数 $F_Z(z)$ ，即
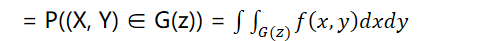
- 其中，G(z) = {(x, y) : g(x, y) ≤ z}
- 当 z ∉ R(Z) 时， $f_Z(z)$ = 0；当 z ∈ R(Z) 时， $f_Z(z)$ = $F_Z(z)$
注
- 在几何上，z= f (x,y)表示空间一个曲面，介于它和xoy平面的空间区域的体积为1
- P((X,Y)∈ G)等于以G为底，以曲面z= f(x, y)为顶面的柱体体积。所以(X,Y)落在面积为零的区域的概率为零。
设二维随机变量 (X, Y) 有密度函数 f(x, y)，Z = X + Y, 则对任意 z ∈ R(Z)，有
特别的，当X和Y独立时，有（卷积公式）

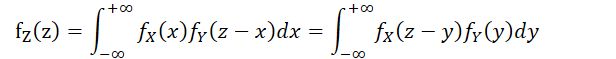
3.5 多维随机变量

1. n维分布函数

n 维随机变量 ( $X_1, X_2, ...X_n$ )： $X_1, X_2, ...X_n$ 是定义在同一个样本空间 Ω 上的随机变量
n 维分布函数：对 n 个实数 $x_1, x_2,...,x_n$ ，有n 维随机变量 ( $X_1, X_2, ...X_n$ n)的n元函数
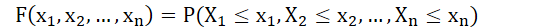
- 具有二维分布函数的性质
若对任意实数 $x_1, x_2,...,x_n$ , 有 F(𝐱𝟏, 𝐱𝟐,…,𝐱𝐧) = $F_1(x_1)F_2(x_2)...F_n(x_n)$ ，则称随机变量 $X_1, X_2, ...X_n$ 相互独立

2. 多维离散型随机变量

n 维概率分布：
- 性质
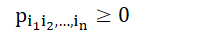
- 随机变量 $X_1, X_2, ...X_n$ 相互独立当且仅当

多项分布：在 N 重独立试验中，若每次试验有 n + 1 种可能结果 $A_1, A_2,...,A_{n+1}$ ，且 $0<\mathrm{p}_{\mathrm{i}}=\mathrm{P}\left(\mathrm{A}_{\mathrm{i}}\right)<1, \mathrm{i}=1,2, \ldots, \mathrm{n}+1, \sum_{i=1}^{n+1} p_{i}=1$ 。令Xi表示N冲独立重复实验中Ai发生的次数，i=1,2,…,n，则( $X_1, X_2, ...X_n$ )所服从的分布称为为多项分布，记为

二项分布的可加性：设 X ∼ B(n, p)，Y ∼ B(m, p)，且 X 与 Y 相互独立，则

Z = X + Y ∼ B(m + n, p)

离散卷积公式： $\mathrm{P}(\mathrm{X}+\mathrm{Y}=\mathrm{k})=\sum_{r} P(X=r) P(Y=k-r)$
推论1：设 $\mathrm{X}_{\mathrm{i}} \sim \mathrm{B}\left(\mathrm{n}_{\mathrm{i}}, \mathrm{p}\right), \mathrm{i}=1,2, \ldots, \mathrm{n}$ ，且 $X_1, X_2, ...X_n$ 相互独立，则
推论2：设 $X_1, X_2, ...X_n$ 独立同分布于 0 − 1 分布 B(1, p)，则

泊松分布的可加性
- 定理：设 X ∼ P( $\lambda_1$ ), Y ∼ P( $\lambda_2$ )，且 X 与 Y 相互独立，则
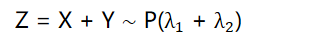
- 推论：设X ∼ P( $\lambda_i$ )，i = 1, 2, . . . , n，且 $X_1, X_2, ...X_n$ 相互独立，则

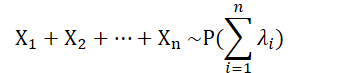
3. 多维连续型随机变量

n 维连续型随机变量： $X_1, X_2, ...X_n$
n 维概率密度函数：f()
- 性质
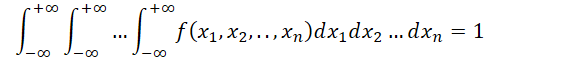
n 维随机变量的分布函数
定理：( $X_1, X_2, ...X_n$ )有 n 维密度函数𝑓( $x_1, x_2,...,x_n$ )， $X_i$ 有边缘密度 $f_i(x_i)$ ， i = 1, 2, . . . , n，则 $X_1, X_2, ...X_n$ 相互独立当且仅当

在各密度函数的公共连续点上成立

n 维均匀分布：G 是 Rn 中一个可求度量的区域，当 n 维随机变量( $X_1, X_2, ...X_n$ )有密度函数

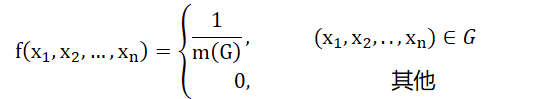
其中, m(G) 为 G 的度量, 称( $X_1, X_2, ...X_n$ )服从 G 上的均匀分布

Γ 分布的可加性：设随机变量 $X_i$ ~Γ( $\alpha_i$ , 𝛽), i = 1, 2, . . . , n，且 $X_1, X_2, ...X_n$ 相互独立，则

最大值和最小值的分布
- 设随机变量 $X_1, X_2, ...X_n$ 独立，且Xi有分布函数(x), i = 1, 2, . . . , n
  - M=max⁡( $X_1, X_2, ...X_n$ )
  - N =min⁡( $X_1, X_2, ...X_n$ )
- 特别的，若 $X_1, X_2, ...X_n$ 独立同分布于 F(x)，那么