| 题目 | Rotamer-free protein sequence design based on deep learning and self-consistency |
|---|---|
| 作者/机构 | 刘海燕组 |
| 期刊/年份 | nature computational science |
| 状态 | 阅读中 |
| DOI | https://doi.org/10.1038/s43588-022-00273-6 |
| Github | https://doi.org/10.24433/CO.3351944.v1 |
摘要
先前提出的几种深度学习方法用于设计氨基酸序列,这些氨基酸序列可以自主折叠成给定的蛋白质骨架,在计算测试中产生了有希望的结果,但在湿实验中表现不如传统的基于能量函数的方法。提出了ABACUS-R方法,该方法使用一个使用多任务学习策略训练的编码器-解码器网络,从中心残基的三维局部环境中预测其侧链类型,除了其他特征外,还包括周围侧链的类型,但不包括其构象。这消除了重建和优化侧链结构的需要,并大大简化了序列设计过程。因此,迭代地将编码器-解码器应用于不同的中心残基能够为目标主干产生自恰的总体序列。
蛋白质的结构可以分为主链和侧链两部分,其中主链包含氨基酸的骨架,而侧链则是与主链相连的分支部分。在蛋白质的折叠和结构稳定性中,侧链的构象起着关键的作用。
Introduction
计算蛋白质设计带来了设计新蛋白质的能力,去满足各种结构和功能的需要。计算蛋白质设计的一个挑战是蛋白质逆向折叠,即选择能够自主折叠成给定主链目标的氨基酸序列。尽管现有一些方法已被实验反复验证,但是仍然有一些不足,例如低成功率、对目标结构的高敏感性以及设计序列单一,缺乏天然序列的多样性和可变性。
传统的蛋白质逆向折叠方法是基于优化侧链类型(和侧链构象)的经验能量函数,**能量函数是基于物理的和从数据中统计学习的。**这些能量函数总是采用近似的方法,将复杂的多体分子相互作用视为一体和二体项的线性组合。尽管传统的能量函数不断改进,但这种近似一直是一个基本的精度限制因素。
先前开发的统计能量模型ABACUS,虽然ABACUS中的能量项被设计为考虑各种物理因素之间的高阶耦合,但耦合效应的非线性积分仅限于单残差和残差对水平,超过这两个水平,单独学习的能量项只能以线性方式组合。将线性组合替换为一种可以集成高阶非线性耦合的方法可以大大提高这种数据驱动方法的鲁棒性和准确性。
一个不依赖于线性组合近似的合适方法是深度学习,最近的一些研究探讨了它在基于结构的序列设计(即逆折叠)中的应用。尽管在计算测试中已经证明有希望的方法优于传统的基于能量函数的方法,但在湿法实验中,深度学习方法尚未表现出与现有的基于能量函数的方法相当的性能( Structure-based protein design with deep learning. )。预计一种发展良好的深度学习方法能够在硅测试和湿实验中优于传统的统计能量模型。
Results
Overview of the model
方法包括两个部分:预训练的编码器-解码器网络,用于从一个三维蛋白质结构的局部环境中推断一个中心残基的侧链类型(Fig1A),以及应用该编码器-解码器更新给定主干中每个残基侧链类型以获得自洽整体序列(从随机初始序列开始)的迭代过程(图1b)。这两个部分结合在一起,整体方法实际上是一个基于主干的序列生成器或编码器,将主干结构编码成氨基酸序列。

图1:ABACUS-R方法概述a、编码器-解码器模型的框架。编码器的输入包括仅骨干结构特征和周围残基的侧链类型(残基邻域建模)。编码器是一个由12块组成的变压器,其输出构成输入特征(局部环境表示)的一般集成表示。为了从多任务学习中获益,该表示被解码为中心残差(解码中心节点)的几个不同属性(包括侧链类型)。b、设计自洽整体序列的迭代方法。在每次迭代中,编码器-解码器网络应用于随机选择的残基子集中的每个残基,根据其当前序列依赖的局部环境更新其侧链类型。
单个残基的编码-解码准确性
一组非冗余蛋白质数据库(PDB)结构已被用于训练编码器-解码器网络。我们通过不同的两种方法划分PDB结构为训练集和测试集来训练两组不同的参数。第一组参数( M o d e l e v a l Model_{eval} Modeleval)通过使用约95%的结构进行训练,其余5%用于测试来学习,用于测试的结构属于数据集中的单域拓扑类(根据CATH 4.2对蛋白质结构的分类),因此测试结构与训练结构都不属于相同的CATH拓扑;因此, M o d e l e v a l Model_{eval} Modeleval可以用于无偏计算评估。第二组参数( M o d e l f i n a l Model_{final} Modelfinal)是通过将蛋白质结构随机分成大约95%用于训练和5%用于测试来学习的,而不考虑它们的CATH结构分类。由于 M o d e l f i n a l Model_{final} Modelfinal是在更完整的数据上进行训练的,因此有望在未来的实际应用中得到应用。
蛋白质的单域拓扑类指的是蛋白质中单一结构域的三维结构分类。
蛋白质的结构域可以被分类为以下几种主要类型:
全α-螺旋结构域:这类结构域主要由α-螺旋组成。
全β-折叠结构域:这类结构域主要由β-折叠(β-纤维或β-板)组成。
α/β结构域:这类结构域含有α-螺旋和β-折叠混合排列,通常β-折叠位于核心,α-螺旋环绕在外围。
α+β结构域:这类结构域中,α-螺旋和β-折叠分开排列,不像α/β结构域那样交替排列。
编码器-解码器采用多任务学习进行训练,其中除其侧链类型外,还使用中心残基的几个属性作为解码目标。Modeleval对各种属性的解码精度报告在图2a-c中
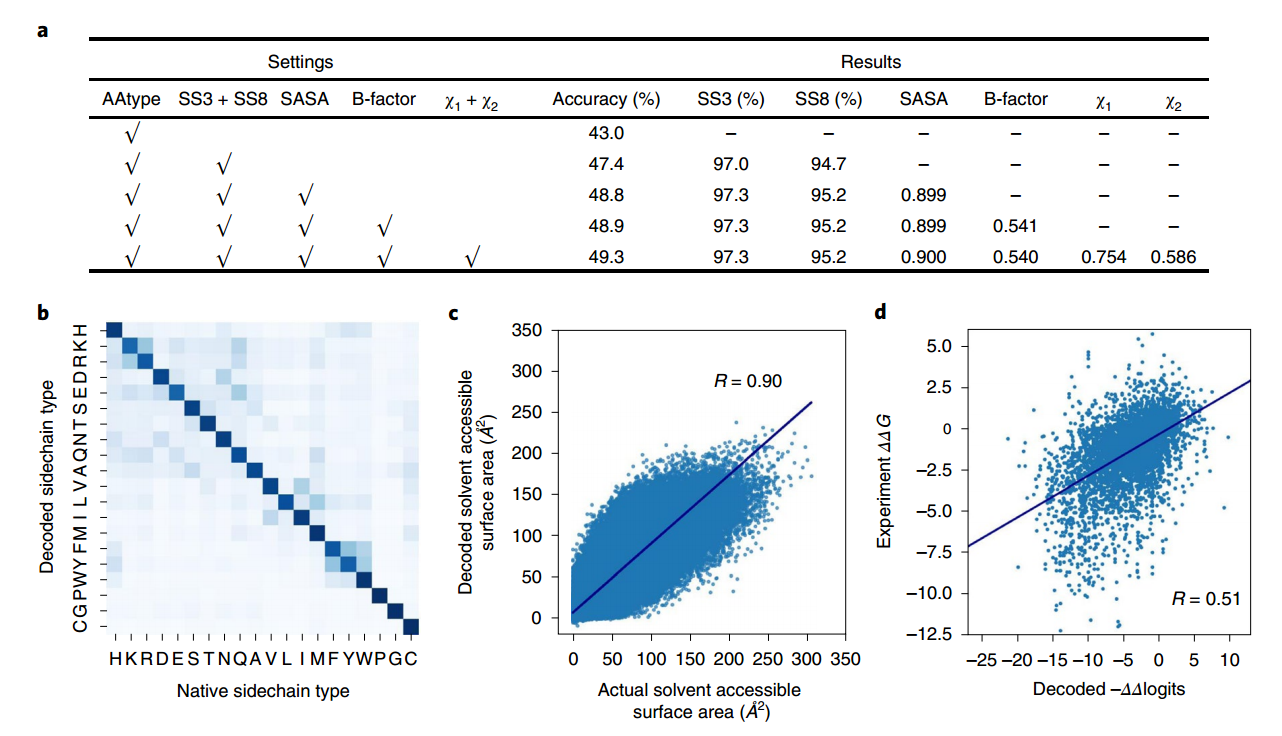
Modeleval和Modelfinal都能恢复中心残差的侧链类型,准确率在50%左右。此外,对于大部分解码结果没有恢复准确的天然侧链类型,解码器产生的侧链类型物理化学上与天然类型相似(例如,赖氨酸(K)为精氨酸(R),苯丙氨酸为酪氨酸等;见图2b)。考虑训练侧链类型以外的属性大大提高了解码侧链类型的准确性(图2a,从45.3%到49.3%的Modeleval),可能是通过补偿训练(自然)序列中的“噪声”(也就是说,本地侧链类型并不总是给定主干的最佳选择)。
对于分类侧链类型属性,解码器的实际输出是一个logits值的向量(请参阅方法)。为了检验logits值的负值是否可以解释为特定局部三维环境中不同残基类型的有效能量,我们选择了一个实验测量蛋白质稳定性变化的蛋白质突变体数据集(ProTherm数据集38),并检验了不同突变体的稳定性变化(通过ΔΔG测量)与- ΔΔlogits变化之间的相关性(见方法);结果如图2d所示。
Method
三维局部环境建模
输入包括一个中心残基的所有结构邻近残基的侧链类型(不使用中心残基的侧链类型)和三维主干结构信息。根据Cα - Cα距离,将构成中心残基三维局部环境的残基集合定义为其k近邻残基。作为编码的输入,我们考虑到每个邻近残基的三种类型特征。
相对中心残基的位置和方向( X S P A X_{SPA} XSPA)
相对中心残基的序列位置( X R S P X_{RSP} XRSP)
侧链类型( X A A X_{AA} XAA)
相对中心残基的位置和方向( X S P A X_{SPA} XSPA)
- 从周围残基残基到中心残基的Cα - Cα来定义
- 周围残基Cα 在中心残基的主链N、Cα 、C原子所定义的局部坐标系中的笛卡尔坐标系(该坐标系,Cα位于原点,Cα-N方向为X轴,N-Cα -C平面对应x-y平面)
- 刚体旋转,对中心和周围残差的两个局部坐标框架的方向进行对齐。使用一组以 0 到 20Å 范围内的 16 个距离值为中心的高斯径向基函数,将 Cα−Cα 距离映射到由 16 个分量组成的向量;笛卡尔坐标按原样使用;刚体旋转被映射到一个三维矢量,其方向对应于旋转轴,其长度对应于旋转角度的大小。在这些映射之后,每个残基的 X S P A X_{SPA} XSPA 是一个由 22 个实值分量组成的向量。
相对中心残基的序列位置( X R S P X_{RSP} XRSP)
X R S P X_{RSP} XRSP的分量是根据邻近残基与中心残基的位置索引之间的差异来定义的, △ i = i − i c e n t r a l \bigtriangleup i=i-i_{central} △i=i−icentral. X R S P X_{RSP} XRSP是一个one-hot向量,编码129个状态, △ i \bigtriangleup i △i从–64到+63的每个整数值对应128个状态之一,其余一个状态编码对应相应的相邻残基是否不在同一条肽链上作为中心残基。
侧链类型( X A A X_{AA} XAA)
X A A X_{AA} XAA 是一个 one-hot 向量,**编码 20 种侧链类型(有20种氨基酸,每种氨基酸侧链不同,所以有20种侧链)**以及一种特殊的 MASKED 类型(对于中心残基,请参见下文)。
中心残基的特征
中心残基的特征被映射到与相邻残基相同维度的向量,只是其 X S P A X_{SPA} XSPA向量的所有分量均为零,并且其 X A A X_{AA} XAA值被映射到MASKED类型。除此之外,还考虑了以中心残基( X B B X_{BB} XBB)为中心的主链构象。 X B B X_{BB} XBB的分量是15个主链扭转角 ψ i − 2 , ψ i − 2 , ω i − 2 ⋯ ψ i + 2 , ψ i + 2 , ω i + 2 ψ_{i−2}, ψ_{i−2}, ω_{i−2}⋯ψ_{i+2}, ψ_{i+2}, ω_{i+2} ψi−2,ψi−2,ωi−2⋯ψi+2,ψi+2,ωi+2,其中 i i i是中心残基的位置索引。将角度除以 π 以获得 [−1,+1) 中的值。为了保持编码中心残基和邻近残基的向量具有相同的输入维度,还考虑所有邻近残基的 X B B X_{BB} XBB 向量,但它们所有分量的值均为零。
对输入特征进行变换
为了从上述原始特征向量产生transformer编码器的输入特征。对One-hot编码特征向量
X
A
A
X_{AA}
XAA和
X
R
S
P
X_{RSP}
XRSP进行线性变换。作为实值分量的
X
S
P
A
X_{SPA}
XSPA和
X
B
B
X_{BB}
XBB通过线性层进行变换。得到向量
E
A
A
,
E
R
S
P
,
E
S
P
A
,
E
B
B
E_{AA},E_{RSP},E_{SPA},E_{BB}
EAA,ERSP,ESPA,EBB,在将它们进行拼接得到
E
E
E
E
A
A
=
W
A
A
X
A
A
E
R
S
P
=
W
R
S
P
X
R
S
P
E
S
P
A
=
W
S
P
A
X
S
P
A
+
b
S
P
A
E
B
B
=
W
B
B
X
B
B
+
b
B
B
E
=
[
E
A
A
,
E
R
S
P
,
E
S
P
A
,
E
B
B
]
\mathbf{E}_{AA}=\mathbf{W}_{AA}\mathbf{X}_{AA} \\ \mathbf{E}_{RSP}=\mathbf{W}_{RSP}\mathbf{X}_{RSP} \\ \mathbf{E}_{SPA}=\mathbf{W}_{SPA}\mathbf{X}_{SPA}+\mathbf{b}_{SPA} \\ \mathbf{E}_{BB}=\mathbf{W}_{BB}\mathbf{X}_{BB}+\mathbf{b}_{BB}\\ \mathbf{E}=[\mathbf{E}_{AA},\mathbf{E}_{RSP},\mathbf{E}_{SPA},\mathbf{E}_{BB}]
EAA=WAAXAAERSP=WRSPXRSPESPA=WSPAXSPA+bSPAEBB=WBBXBB+bBBE=[EAA,ERSP,ESPA,EBB]
基于transformer的编码器结构
所有残基的的
E
E
E向量集合为
E
n
,
n
=
0
,
1
,
2
,
.
.
.
k
{E_{n},n=0,1,2,...k}
En,n=0,1,2,...k,其中
E
0
E_0
E0为中心残差的向量。
如图1所示,将这组矢量送到12块的transformer中。transformer各块依次由多头自关注模块、层归一化变换、前馈模块和第二层归一化变换组成,公式如下:
F
n
0
=
E
n
,
Q
n
i
=
W
i
Q
F
n
i
,
K
n
i
=
W
i
K
F
n
i
,
V
n
i
=
W
i
V
F
n
i
,
F
n
′
i
=
LN
(
F
n
i
+
MHA
(
Q
n
i
,
{
K
m
i
,
V
m
i
;
m
=
0
,
1
,
2
,
…
,
k
}
)
)
,
F
n
i
+
1
=
LN
(
F
n
′
i
+
FFN
(
F
n
′
i
)
)
,
\mathbf{F}_{n}^{0}=\mathbf{E}_{n}, \\ \mathbf{Q}_{n}^{i}=\mathbf{W}_{i}^{Q} \mathbf{F}_{n}^{i}, \mathbf{K}_{n}^{i}=\mathbf{W}_{i}^{K} \mathbf{F}_{n}^{i}, \mathbf{V}_{n}^{i}=\mathbf{W}_{i}^{V} \mathbf{F}_{n}^{i}, \\ \mathbf{F}_{n}^{\prime i}=\operatorname{LN}\left(\mathbf{F}_{n}^{i}+\operatorname{MHA}\left(\mathbf{Q}_{n}^{i},\left\{\mathbf{K}_{m}^{i}, \mathbf{V}_{m}^{i} ; m=0,1,2, \ldots, k\right\}\right)\right), \\ \mathbf{F}_{n}^{i+1}=\operatorname{LN}\left(\mathbf{F}_{n}^{\prime i}+\operatorname{FFN}\left(\mathbf{F}_{n}^{\prime}{ }^{i}\right)\right),
Fn0=En,Qni=WiQFni,Kni=WiKFni,Vni=WiVFni,Fn′i=LN(Fni+MHA(Qni,{Kmi,Vmi;m=0,1,2,…,k})),Fni+1=LN(Fn′i+FFN(Fn′i)),
其中
i
=
1
−
12
i=1-12
i=1−12表示transformer的块
解码器和训练损失
编码器-解码器网络采用多任务学习策略进行训练,中心残基的多个属性同时被视为解码目标,包括侧链类型、二级结构状态、溶剂可达表面积(SASA)、侧链扭角(即χ1和χ2)以及主链原子总数的结晶学B因子。对于二级结构状态,DSSP程序使用的三态和八态方案已同时考虑。对于侧链扭转,我们只考虑χ1和χ2,而不考虑χ3或χ4,因为只有当与正确和准确的χ1和χ2相关联时,χ3或χ4才能用于编码侧链结构。
侧链类型、二级结构状态、溶剂可达表面积(SASA)、侧链扭角(即χ1和χ2)以及主链原子总数的结晶学B因子
在训练自然序列中所谓的真基侧链类型标签实际上是相当有噪声的,因为本地侧链类型并不总是给定结构的最佳选择。辅助任务引入的归纳偏置可以帮助降低编码器-解码器网络的Rademacher复杂度或其适应这些噪声的能力。二级结构状态和SASA辅助任务有望引入有用的归纳偏差,因为它们会强烈影响侧链类型偏好。中心残基的侧链构象被认为是辅助任务,因为它们被认为与周围侧链的构象相关。因此,它们可以隐式地帮助在输出表示中保留有关本地环境的更多结构信息。出于类似的原因,也包含了 B-factor。
通过将
F
0
12
F_0^{12}
F012传递到不同的感知器网络(解码器)来解码中心残基的不同属性,每个解码器网络具有单个隐藏层。
真基侧链类型标签的噪声:在蛋白质结构预测中,侧链类型标签(即每个氨基酸侧链的化学性质)是重要的信息。然而,这些标签可能包含噪声,意味着给定的侧链类型不总是与蛋白质的实际结构最匹配的。这种噪声可以来源于实验数据的不精确性、结构预测的误差,或是自然序列的多样性和复杂性。
降低Rademacher复杂度:Rademacher复杂度是衡量学习模型容量(或复杂度)的一种方式,与模型对噪声的适应能力有关。通过引入辅助任务和相应的归纳偏差,可以降低模型的Rademacher复杂度,意味着减少模型对训练数据中噪声的过度拟合,从而提高其泛化能力。
对于侧链类型解码器,其输出层有20个感知机节点,使用softmax转换输出值logits为20个侧链类型归一化的概率,对于侧链a:
P
a
=
e
l
o
g
i
t
s
a
/
∑
b
20
e
l
o
g
i
t
s
b
P_a=e^{logits_a}/\sum_{b}^{20}e^{logits_b}
Pa=elogitsa/∑b20elogitsb.
交叉熵损失函数:
L
A
A
=
−
∑
a
=
1
20
y
a
l
o
g
(
p
a
)
L_{AA}=-\sum_{a=1}^{20}y_alog(p_a)
LAA=−∑a=120yalog(pa),其中 a 是侧链类型索引,
y
=
(
y
0
,
y
1
,
⋯
,
y
20
)
y=(y_0, y_1,⋯, y_{20})
y=(y0,y1,⋯,y20) 是由真实标签产生的 one-hot 向量,
p
=
(
p
0
,
p
1
,
⋯
,
p
20
)
p=(p_0, p_1,⋯, p_{20})
p=(p0,p1,⋯,p20) 是预测概率的向量.
二级结构状态的解码器和损失的定义方式与侧链类型相同。同时使用三态和八态分类方案。交叉熵损失分别记为LSS3和LSS8。对于包括 SASA 和 X 射线 B 因子在内的数值属性,我们首先使用从训练数据计算出的平均值和标准差对属性进行归一化。相应的解码器回归归一化属性。损失 LSASA 和 LBfactor 定义为回归的 L1 误差。
L1 误差: 也称为L1范数损失或绝对值损失,用于衡量预测值和实际值之间的差异。L1误差的计算公式为:
L 1 = ∑ i = 1 n ∣ y i − y i ^ ∣ L1= {\textstyle \sum_{i=1}^{n}} \left |y_i-\hat{y_i}\right | L1=∑i=1n∣yi−yi^∣
L1误差对于异常值(离群点)的敏感度较低在存在异常值的数据集中,使用L1误差作为损失函数可能是一个更好的选择
多任务学习的总损失为:
L
=
L
A
A
+
λ
1
(
L
S
S
3
+
L
S
S
8
)
+
λ
2
L
S
A
S
A
+
λ
3
L
B
f
a
c
t
o
r
+
λ
4
(
L
χ
1
+
L
χ
2
)
L = L_{AA}+\lambda_1(L_{SS3}+L_{SS8})+\lambda_2L_{SASA}+\lambda_3L_{Bfactor}+\lambda_4(L_{\chi_1}+L_{\chi_2})
L=LAA+λ1(LSS3+LSS8)+λ2LSASA+λ3LBfactor+λ4(Lχ1+Lχ2)
其中 $
λ
1
−
4
λ_{1−4}
λ1−4 是平衡不同损失的权衡参数。由于最终解码精度对这些参数的确切值并不敏感,文中没有对权衡参数的各种组合进行广泛的探索。相反,从较小的起始值开始单独逐渐增加各个 λ 参数,直到相应属性的解码精度最大化,而侧链类型的解码精度没有降低。
自洽迭代
为了设计给定目标主链的完整序列,我们从初始序列开始,为所有残基随机选择侧链类型。在每次迭代中,我们随机选择若干残基,将每个残基作为中心残基,将预训练好的编码器-解码器网络应用于其当前的三维局部环境,并根据(侧链型)解码器的输出更新中心残基的侧链类型。在一次迭代中,所有选定残基的计算都是并行执行的,以利用并行计算的优势。并行侧链类型更新所选残基的初始数量设定为序列长度的 80%,这一数量在随后的迭代中逐渐减少,直到最后的迭代中逐一考虑残基。
在迭代过程中,我们会监测不断演化的序列的总 -logP 值,其定义为:
−
l
o
g
P
t
o
t
a
l
=
∑
i
=
1
L
−
l
o
g
P
a
i
i
-logP_{total}=\sum_{i=1}^{L}-logP_{a_i}^i
−logPtotal=∑i=1L−logPaii
其中L为序列长度,i为残基索引,
a
i
a_i
ai为在序列中第i个位置的侧链类型索引。
P
a
i
i
P_{a_i}^i
Paii为编码解码网络根据残基i的当前局部环境(取决于i的邻近残基的当前侧链类型)预测相应侧链类型的概率。
为了简单起见,本研究的所有设计运行种都使用了固定的 1,000 自洽迭代步数,在所有设计运行中,最低 -logP 值始终是以更少的步骤达到。

在生成用于湿法实验检验的序列时,采用了两种不同的迭代协议来更新中心残基的侧链类型。在第一个“正常”协议中,总是选择最大概率的侧链类型(由相应的解码器预测)。该方案用于产生最大自一致的整体序列,经第一批实验检验。在第二种协议中,根据从编码器输出导出的概率分布对侧链类型进行采样。为了控制采样侧链类型的多样性,我们使用以下公式将解码器预测的原始分布映射为新的分布:
p
a
′
=
(
p
a
)
a
/
∑
b
=
1
20
(
p
b
)
a
p_{a}^{'}=(p_a)^a/\sum_{b=1}^{20}(p_b)^a
pa′=(pa)a/∑b=120(pb)a
参数α的值控制了被采样侧链类型的多样性:当α的正值很大时,第一协议和第二协议变得等效;减小α值会增加设计序列的多样性,但也会导致−logits度量增加(补充图21)。为了设计用于第二批实验的序列(为相同目标设计的序列具有约60%的序列间同一性),我们使用α值为1.5,这仍然导致−logits值低于本地序列(补充图21)。

























 2489
2489

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








