机器人学基础--位形空间（二）

机器人学基础

一、位形空间

1.1 刚体的自由度

（1）机器人在哪？
位形(Configuration)：机器人身上所有的点的位置。
位形空间（C-sapce）：表示所有位形的空间。
C-sapce维度就是机器人自由度(dof)，也是表达位形所需最少的实数个数。
（2）如何计算机器人自由度？
机器人由刚性连杆（刚体）构成，通过关节连接，所以组成机器人的刚体自由度就是机器人自由度。
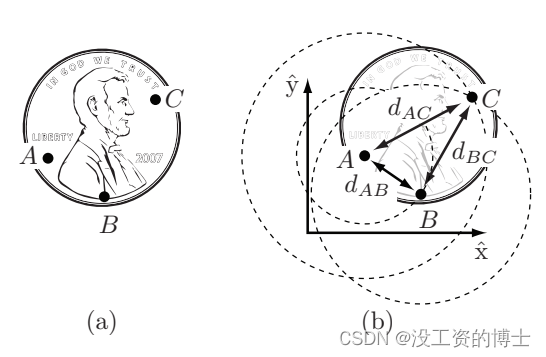
（3）二维空间刚体自由度
step1：选择平面上一个点$A(x_a,y_a)$.
step2：再选择平面上一点$B(x_b,y_b)$，因为是刚体所以AB之间距离$d_{AB}$ 恒定，所以点B必须位于以A为圆心，以$d_{A}B$ 为半径的圆上。这就给点B增加了1个独立约束。
step3：再选择平面上一点$C(x_C,y_C)$，因为是刚体所以AC,BC之间距离$d_{AC},d_{BC}$恒定，所以点C必须位于以A为圆心，以$d_{AC}$为半径的圆和以B为圆心，以$d_{BC}$为半径的圆上。这就给点C增加了2个独立约束。

（4）3维空间刚体自由度
step1：选择平面上一个点$A(x_a,y_a,z_a)$.
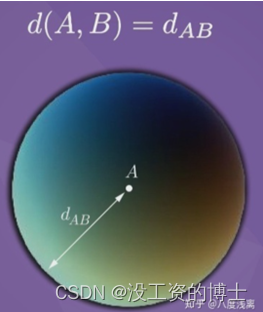
step2：再选择平面上一点$B(x_b,y_b,z_b)$，因为是刚体所以AB之间距离d_AB 恒定，所以点B必须位于以A为球心，以$d_{AB}$为半径的球面上。这就给点B增加了1个独立约束。
step3：再选择平面上一点$C(x_C,y_C,z_C)$，因为是刚体所以AC,BC之间距离$d_{AC},d_{BC}$ 恒定，所以点C必须位于以A为球心，以$d_{AC}$ 为半径的球面和以B为球心，以$d_{BC}$ 为半径的圆面上。这就给点C增加了2个独立约束。
step4：再选择平面上一点$D(x_C,y_C,z_C)$，点C增加了3个独立约束。
dof=质点的自由度之和-质点的独立约束之和
=9-3=6
同理四维空间刚体自由度为10

1.2 机器人的自由度

机器人是由刚性连杆（刚体）构成，通过关节连接。对于一个没有约束的刚体而言，在平面上dof为3，三维空间自由度为6。如果使用关节对机器人进行连接，则刚体往往会受到关节的约束。所以机器人的自由度dof：

(1) 了解一下常用关节的自由度：

(2)Grubler公式

m为自由度数
N为包含基座的构件个数
J为关节数
$c_i$为关节提供的独立约束个数
$f_i$ 为关节的自由度数
注：每一个关节都是独立的。如果关节的约束不是相互独立，Grubler提供的是自由度数目是一个下界。

(3)两个小例子


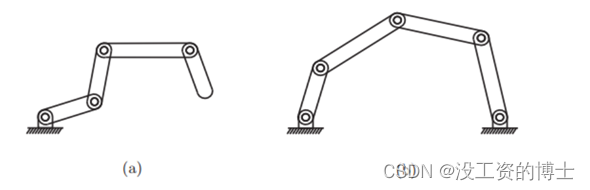
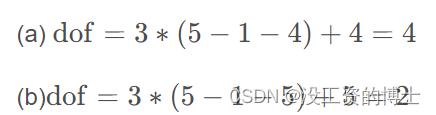
参考链接: https://www.guyuehome.com/36940
参考链接：https://www.bilibili.com/video/BV1KV411Z7sC/?p=4

1.3 位形空间的拓扑

如果两个表面能够连续从一种形状变化到另一种形状，而不经过切割和粘结等方式，我们称他们为拓扑等效的。在二维面中，球面（球是三维的，球面是二维的（可由经度与纬度表示））若想变为一个平面，则需要进行切割，故其不是拓扑等效。

来看一个圆环面变为一个茶杯面:

1.4 位形空间的表示

一切变化来源于表面自身而不用任何特殊的处理。故其为拓扑等效的。在一维空间中，不同的拓扑为：圆、直线、线段。在二维空间中，不同的拓扑为：平面、球面、圆环面、圆柱面。四种具有不同拓扑结构的二维C-空间及其坐标表示：

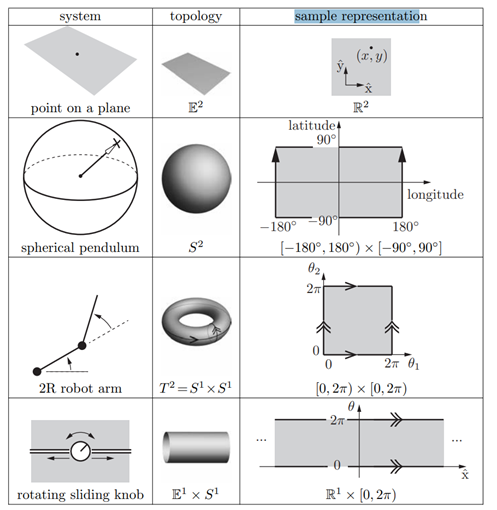
需要记住的是表达与空间拓扑本身是独立的，即不同的表达并不能影响空间拓扑结构本身。
（1）位形空间的表达由两种方式：显式参数化和隐式表示。
显示参数化可以使用最少的参数来表示n维空间，但在将一些非欧空间式用坐标表示时会出现如上面例子中一些不连续等问题的奇异(singularity)情况。使用隐式表示而不是显式参数化。一个隐式表示把n 维空间看成是内含与大于n维的空间的欧拉空间。例如2维球面可以看成是包含于3维欧拉空间的一个面。一个隐式表示使用的坐标数高于该空间的维度，当需要约束冗余的自由度。将n维C-space空间看作是嵌入到超过n维欧氏空间中(需要添加约束条件)，例如，2维的单位球面可以看成是嵌入在3维欧氏空间的一个球面，该三维表示满足约束条件：

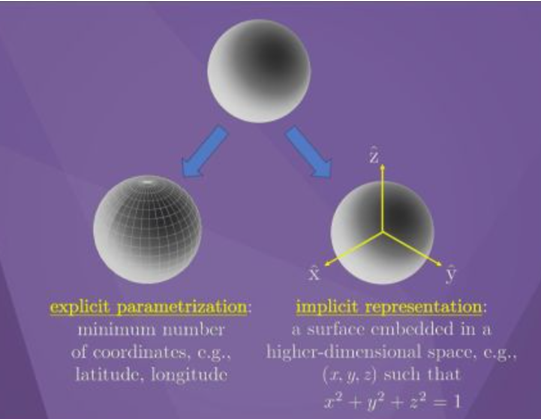
在这里插入图片描述一般都采用隐式法。

1.5 速度约束与位形约束

对于平面四连杆闭环机器人，其自由度为1，C-空间维度为1，位形由四个关节角${\theta }_1,\dots ,{\theta }_4$ 表示。根据隐式表示，需要三个独立约束条件。可以找到这样3个独立约束方程，并且只有一个未知数。此时可以将该机器人看作是嵌入在4维空间的1维的曲线。那么这约束我们成为完整约束。

现在我们将其一般化，假设机器人的位形由n个变量定义，且机器人受到k个独立的约束，那么机器人的自由度为n-k，那么C空间的维度也为n-k，当机器人开始运动时，这些约束对机器人的速度形成了怎样的限制？

（1）约束矩阵

如果机器人在运动，则角度是关于时间t的函数，对上式两边对t求导数：


写成矩阵相乘的形式:

简化写成：

θ ̇表示角度对时间的变化率即角速度

（2）速度约束方程

• 称为速度约束，上式称为Pfaffian约束。

• 完整约束也称为可积约束，因为完整约束本质是对速度约束的积分（即其速度约束可以通过积分变为等效的位形约束）。

• Pfaffian约束有时并不可积，不可积的Pfaffian约束称为非完整约束。非完整约束减少了可能的速度空间，但并没有减少可能的C-space维度。

完整约束是对位形的约束，非完整约束是对速度的约束。

1.6 工作空间与任务空间

任务空间可以理解为让机器人擦黑板，那么黑板这个平面才是任务空间。工作空间是指当机器人能否完成擦黑板的任务，如果机械臂很短的话，其工作空间可能只是一办的黑板。

参考链接: https://www.guyuehome.com/36940
参考链接：https://www.bilibili.com/video/BV1KV411Z7sC/?p=4