因子图优化原理（iSAM、iSAM2论文解析）

slam问题

在介绍因子图之前，先从一个简单的slam问题入手，如下图所示：

在图中清晰的显示了各个节点和和连接结点边之间的定义，对于图结构不做过多说明，假定读者已经有一定的先验知识。在上图显示的slam问题中，实际上我们要解决的问题就是，从机器人的控制和观测中恢复机器人的路径以及环境地图。

通过贝叶斯网络对slam问题建模

在贝叶斯网络中，通过有向边连接变量，除了路标状态节点和机器人的状态节点外（两个状态节点为状态变量），还定义了路标观测节点（红色）和运动观测节点（绿色）（两个观测节点为观测变量）。这个贝叶斯实际上描述了一种状态和观测的联合概率模型。假设知道系统的状态变量X（机器人所在位置、路标点所在位置），可以推测出机器人得到的观测量Z（观测量是通过某些传感器得到的，而传感器有已知模型，可以通过数据手册得到），即已知机器人的状态量和传感器的模型，就可以推算出机器人的观测量。所以得到了如下图所示的一个生成模型：

由于观测量之间相互独立，可以得到下式所述的模型：

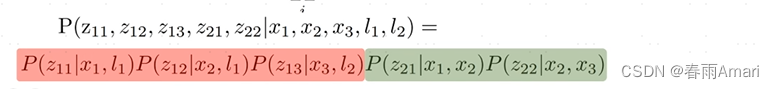
从贝叶斯网络到因子图

基于上文，我们知道贝叶斯网络是一个生成模型，解决的从状态变量得到观测观测变量，而我们的问题是从观测变量来推出状态变量，是一个状态估计问题，这就引出了因子图，因子图是一个inference model。
首先来对问题做一个推导：由于我们要从观测量来推出状态量，这是一个后验概率问题，结合贝叶斯丁玲，问题被描述为最大化一个后验概率问题（MAP），即给定系统系统观测量，求解系统状态量，使得下式的条件概率最大：