本文介绍了椭圆柱坐标系及其与直角坐标系的变换，详细阐述了共焦椭圆和双曲线的方程。接着，探讨了长旋转椭球体坐标系，包括其坐标变换公式，并与直角坐标系的关系。
椭圆柱坐标（Elliptic Cylindrical Coordinates）
首先介绍椭圆柱坐标系，其横截面如下：
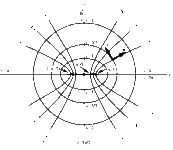
其与直角坐标的变换为：
{ x = a cosh u cos v y = a sinh u sin v z = z \begin{cases} \begin{aligned} x &= a \cosh u \cos v \\ y &= a \sinh u \sin v \\ z &= z \end{aligned} \end{cases} ⎩⎪⎨⎪⎧xyz=acoshucosv=asinhusinv=z
其中， u ∈ [ 0 , + ∞ ) u \in [ 0 , + \infty ) u∈[0,+∞) ， v ∈ [ 0 , 2 π ) v \in [ 0,2 \pi ) v∈[0,2π) ， z ∈ ( − ∞ , + ∞ ) z \in ( - \infty , + \infty ) z∈(−∞,+∞)，且长轴在 x x x轴上。
在 x O y xOy xOy平面上，共焦点的任一椭圆与任一双曲线有4个交点，且对称分布于坐标的4个象限中。通过限定双曲线的渐近线倾角（此处，渐近线应为过原点的射线，其倾角即与 x x x正半轴的夹角），取得双曲线的1/4部分，使得其与椭圆的交点只有1个，即
- v ∈ ( 0 , π / 2 ) v \in (0, \pi/2) v∈(0,π/2)，取双曲线在第Ⅰ象限中的部分；
- v ∈ ( π / 2 , π ) v \in (\pi/2, \pi) v∈(π/2,π)，取双曲线在第Ⅱ象限中的部分；
- v ∈ ( π , 3 π / 2 ) v \in (\pi, 3\pi/2) v∈(π,3π/2)，取双曲线在第Ⅲ象限中的部分；
- v ∈ ( 3 π / 2 , 2 π ) v \in (3\pi/2, 2\pi) v
最低0.47元/天 解锁文章
扫一扫
456
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
