大物热力学基础笔记_1

---

太长不看版

绝热过程方程
① $pd{V}^{\gamma }=c$
② $V^{\gamma -1}T=c_2$
③ $p^{\gamma -1}{T}^{-\gamma }=c_3$

绝热过程做功
$W=-\Delta E=-\frac{i}{2}vRdT=pdV$

热机效率
$\eta =\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}$

卡诺正循环效率
$\eta =1-\frac{T_2}{T_1}$

制冷系数
$\omega =\frac{Q_2}{W}=\frac{Q_2}{Q_1+Q_2}$

卡诺制冷机制冷系数
$\omega =\frac{T_2}{T_1-T_2}$

---

绝热过程

绝热过程

系统与外界无热量交换的过程称为绝热过程，

特征：$dQ=dE+pdV=0$          $dW=-dE=pdV$

绝热过程靠减少内能来对外做功。

故由$\Delta E=\frac{i}{2}vR(T_2-T_1)$         得$W=-\Delta E=-\frac{i}{2}vRdT=pdV$

气体对外做功，内能减少，温度下降，压强减小，该过程$p、V、T$同时变化。

绝热过程摩尔热容：$C_Q=(\frac{dQ}{dT}{)}_Q=0$

---

绝热过程方程推导：

$W=-\Delta E=-\frac{i}{2}vRdT=pdV$$\cdots$ $\cdots$ ①

状态方程：$pV=vRT$

两边微分得：$pdV+Vdp=vRdT$$\cdots$ $\cdots$ ②

①、②消去$dT$得：$\frac{pdV+Vdp}{pdV}=-\frac{R}{C_V}$

$\Rightarrow$ $pdV+Vdp=-\frac{R}{C_V}pdV$

$\Rightarrow$ $Vdp=-(1+\frac{R}{C_V})dV=-\frac{C_p}{C_V}pdV=-\gamma pdV$

故$Vdp=-\gamma pdV$ $\Rightarrow$ $\frac{dp}{p}+\gamma \frac{dV}{V}=0$

两边积分得：$lnp+\gamma lnV=c$ $\Rightarrow$ $pd{V}^{\gamma }=c$ $\cdots$ $\cdots$ ③

由③和状态方程消去$p$得       $V^{\gamma -1}T=c_2$ $\cdots$ $\cdots$ ④（该式是对于某一确定种类和量的气体，故$v$可看作常量）

由③和状态方程消去$V$得       $p^{\gamma -1}{T}^{-\gamma }=c_3$ $\cdots$ $\cdots$ ⑤

③、④、⑤称为绝热过程方程。（$\gamma =\frac{C_p}{C_V}$$>1$）

---

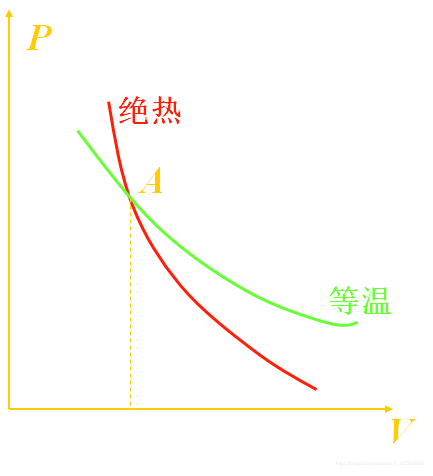
绝热线

绝热线：

由 $p{V}^{\gamma }=c$ 两边微分 $\Rightarrow$ $V^{\gamma }dp+\gamma p{V}^{\gamma -1}dV=0$ $\Rightarrow$ $Vdp+\gamma pdV=0$

故$\frac{dp}{dV}$${|}_A=-\gamma \frac{P_A}{V_A}$

等温线

由 $pV=c$ 两边微分 $\Rightarrow$ $pdV+Cdp=0$ $\Rightarrow$ $\frac{dp}{dV}$${|}_A=-\frac{P_A}{V_A}$

由于$\gamma >1$    故绝热线比等温线陡。

注：绝热线与等温线只有一个交点。

---

气体向真空绝热自由膨胀过程中，由于绝热，$dQ=0$，由因气体向真空自由膨胀，故$dW=0$。由此可得$dE=0$。即理想气体向真空自由膨胀后内能不变，即温度不变。且$p_1{V}_1=p_2{V}_2$。

---

卡诺循环

循环过程：系统经过一系列状态变化后又回到初始状态的整个过程叫循环过程。

循环过程的物质系统统称为工作物质（工质）。

循环中由于内能为状态量，故变化始末$\Delta E=0$。

---

正循环

正循环过程 $W>0$ 。

净功 $W$ 为 $p-V$ 图中的循环面积，且由于$\Delta E=0$，故净热$\Delta Q=W$。

热机效率

$\eta =\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}$（$Q_1、Q_2$分别为 $AaB$ 和 $BbA$ 过程的净热）

由于$Q_2\ne Q_1\ne 0$     故$\eta <1$ 。

---

卡诺循环

卡诺循环由两个绝热过程和两个等温过程构成。工作物质只与两个恒定热源（一个高温一个低温）交换热量。

$A、B$ 过程，等温膨胀吸热，

$Q_1=\frac{m}{M}R{T}_{1}ln\frac{V_2}{V_1}$

$C、D$ 过程，等温压缩放热，

$Q_2=\frac{m}{M}R{T}_{2}ln\frac{V_3}{V_4}$

$BC、DA$ 过程绝热，$Q=0$ 。

故循环效率 $\eta =\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_{2}ln\frac{V_3}{V_4}}{T_{1}ln\frac{V_2}{V_1}}$

绝热过程中：

         $B\to C$：$T_1{V_2}^{\gamma -1}=T_2{V_3}^{\gamma -1}$
         $D\to A$：$T_1{V_1}^{\gamma -1}=T_2{V_4}^{\gamma -1}$

故 $\frac{V_2}{V_1}=\frac{V_3}{V_4}$

可得 $\eta =\frac{W}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1}$

所以卡诺正循环效率为：$\eta =1-\frac{T_2}{T_1}$

---

制冷剂采用的是逆循环。

制冷剂功效用制冷系数 $\omega =\frac{Q_2}{W}=\frac{Q_2}{Q_1+Q_2}$ 来衡量，

对于卡诺制冷机：$\omega =\frac{T_2}{T_1-T_2}$ 。