单相异步电动机的建模仿真（3）基于空间向量和混合磁链数学模型

最新推荐文章于 2024-07-08 07:52:54 发布

一仰众山高

最新推荐文章于 2024-07-08 07:52:54 发布

阅读量920

点赞数 25

文章标签： matlab

本文链接：https://blog.csdn.net/weixin_45670943/article/details/139678323

版权

1. 引言

2. 混合磁链数学模型

3. 基于混合磁链数学模型的Simulink仿真模型

4. 空间向量数学模型

5. 基于空间矢量数学模型的Simulink仿真模型

6. 仿真实例

7. 总结

1. 引言

不同的数学模型形式可以提供不同的视角和分析方法，这对于电机的设计、控制和故障诊断等方面具有重要意义。例如，研究以混合磁链为状态变量的数学模型并因此建立仿真模型就比以电流作为状态变量表示的数学模型和相应的仿真模型的稳定性要好，因为磁链在瞬变过程中变化相对较小，或者说较为稳定，这种模型有助于获得紧凑和稳定的瞬态过程解答。空间向量的数学模型表达形式简洁，因此器对应的simulink仿真模型也非常简洁且仿真速度较快。另外，通过建立不同的数学模型，可以对电机系统的稳定性进行深入分析。例如，三相感应电机的小扰动数学模型可以用于分析系统稳定性，这对于设计和优化电机控制系统至关重要。通过建立通用化、模块化的仿真模型，可以方便地对电机进行各种工况下的仿真研究。例如，基于Matlab/Simulink环境下的S函数感应电机仿真模型，不仅实现了通用化和模块化，还建立了电机模型的库文件，便于用户进行多种仿真实验。

2. 混合磁链数学模型

为简单起见，作如下假设：（1）气隙磁通密度在空间按正弦分布，忽略磁场的高次谐波；（2）电机磁路不饱和；（3）忽略铁心损耗：（4）不考虑频率和温度变化对绕组电阻的影响。选取dq静止坐标系。按电动机惯例写数学方程。

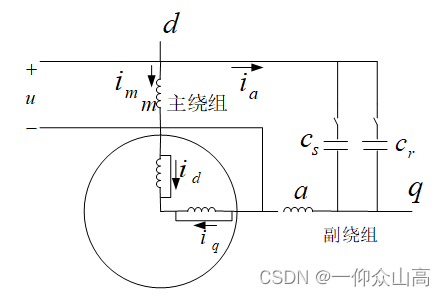
图1 双绕组单相电容异步电动机的接线原理图

（1）磁链方程

$\psi_{m}=L_{m}i_{m}+M_{m}i_{d}\\\psi_{a}=L_{a}i_{a}+M_{a}i_{q}\\\psi_{d}=L_di_d+M_mi_m\\\psi_{q}=L_qi_q+M_ai_a$ （1）

$Lm 、 La 一分别为主绕组和副绕组的全自感 ; Mm 一主绕组与转子 d 轴等效绕组的互感; Ma 一副绕组与转子 q 轴等效绕组的互感; Ld 一折算到主绕组的转子 d 轴等效绕组的全自感； Lq 一折算到副绕组的转子 q 轴等效绕组的全自感。$

（2）电压方程

$\begin{aligned}&u_{m}=R_{m}i_{m}+p\psi_{m}\\&u_{a}=R_{a}i_{a}+p\psi_{a}\\&u_{d}=R_{d}i_{d}+p\psi_{d}+\omega_{r}\psi_{q}/k\\&u_{q}=R_{q}i_{q}+p\psi_{q}-k\omega_{r}\psi_{d}\end{aligned}$ (2)

令混合磁链 $\lambda_{ds}=\omega_{b}\psi_{m};\lambda_{qs}=\omega_{b}\psi_{a};\lambda_{dr}=\omega_{b}\psi_{d};\lambda_{qr}=\omega_{b}\psi_{q},$ 即在方程（1）两边同时乘以角频率 $\omega_b=2\pi f_N$ ，再将其代入式（2），可得

$\begin{aligned}&p\lambda_{ds}=\omega_{b}(u_{ds}+\frac{R_{d}}{x_{ld}}(\frac{x_{m}}{x_{lrd}}\lambda_{dr}+(\frac{x_{m}}{x_{ld}}-1)\lambda_{ds}))\\&p\lambda_{qs}=\omega_{b}(u_{qs}+\frac{R_{q}}{x_{lq}}(\frac{x_{a}}{x_{lrq}}\lambda_{qr}+(\frac{x_{a}}{x_{lq}}-1)\lambda_{qs}))\\&p\lambda_{dr}=\omega_{b}(-\frac{\omega_{r}}{k\omega_{b}}\lambda_{qr}+\frac{R_{rd}}{x_{lrd}}(\frac{x_{m}}{x_{ld}}\lambda_{ds}+(\frac{x_{m}}{x_{lrd}}-1)\lambda_{dr}))\\&p\lambda_{qr}=\omega_{b}(\frac{k\omega_{r}}{\omega_{b}}\lambda_{dr}+\frac{R_{rq}}{x_{lrq}}(\frac{x_{a}}{x_{lq}}\lambda_{qs}+(\frac{x_{a}}{x_{lrq}}-1)\lambda_{qr}))\end{aligned}$ （3）

$\begin{aligned}&\lambda_{mq}=X_{ml}(\frac{\lambda_{qs}}{x_{lq}}+\frac{\lambda_{qr}}{x_{lrq}})\\&\lambda_{md}=X_{al}(\frac{\lambda_{ds}}{x_{ld}}+\frac{\lambda_{dr}}{x_{lrd}})\end{aligned}$ （4）

其中，

$X_{ml}=(\frac1{x_{mq}}+\frac1{x_{lsq}}+\frac1{x_{lrq}})^{-1}\\X_{al}=(\frac1{x_{md}}+\frac1{x_{lsd}}+\frac1{x_{lrd}})^{-1}$

由磁链方程（1），等效的定转子电流可以表示为：

$\begin{aligned}&i_{ds}=\frac{\lambda_{ds}-\lambda_{md}}{x_{id}}\\&i_{qs}=\frac{\lambda_{qs}-\lambda_{inq}}{x_{iq}}\\&i_{dr}=\frac{\lambda_{dr}-\lambda_{ind}}{x_{ird}}\\&i_{qr}=\frac{\lambda_{qr}-\lambda_{mq}}{x_{irq}}\end{aligned}$ （5）

考虑前文（单相异步电动机的建模仿真（1））的电磁转矩表达式，此时电磁转矩方程为：

$T_e=\frac{n_p}{\omega_b}(\psi_{qr}i_{dr}/k-k\psi_{dr}i_{dr})$ （6）

方程（1）~方程（6）即为单相异步电动机的混合磁链数学模型。

3. 基于混合磁链数学模型的Simulink仿真模型

根据双绕组单相电容异步电动机混合磁链数学模型（方程（1）～方程（6）和转子运动方程构造的Simulink仿真模型如图2所示。

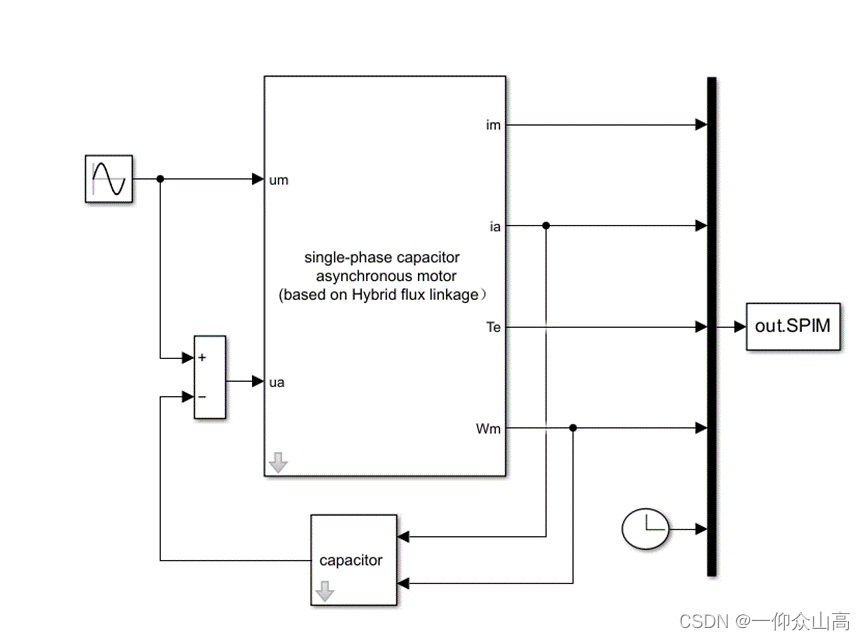
图2 基于混合磁链数学模型的双绕组单相电容异步电动机仿真模型

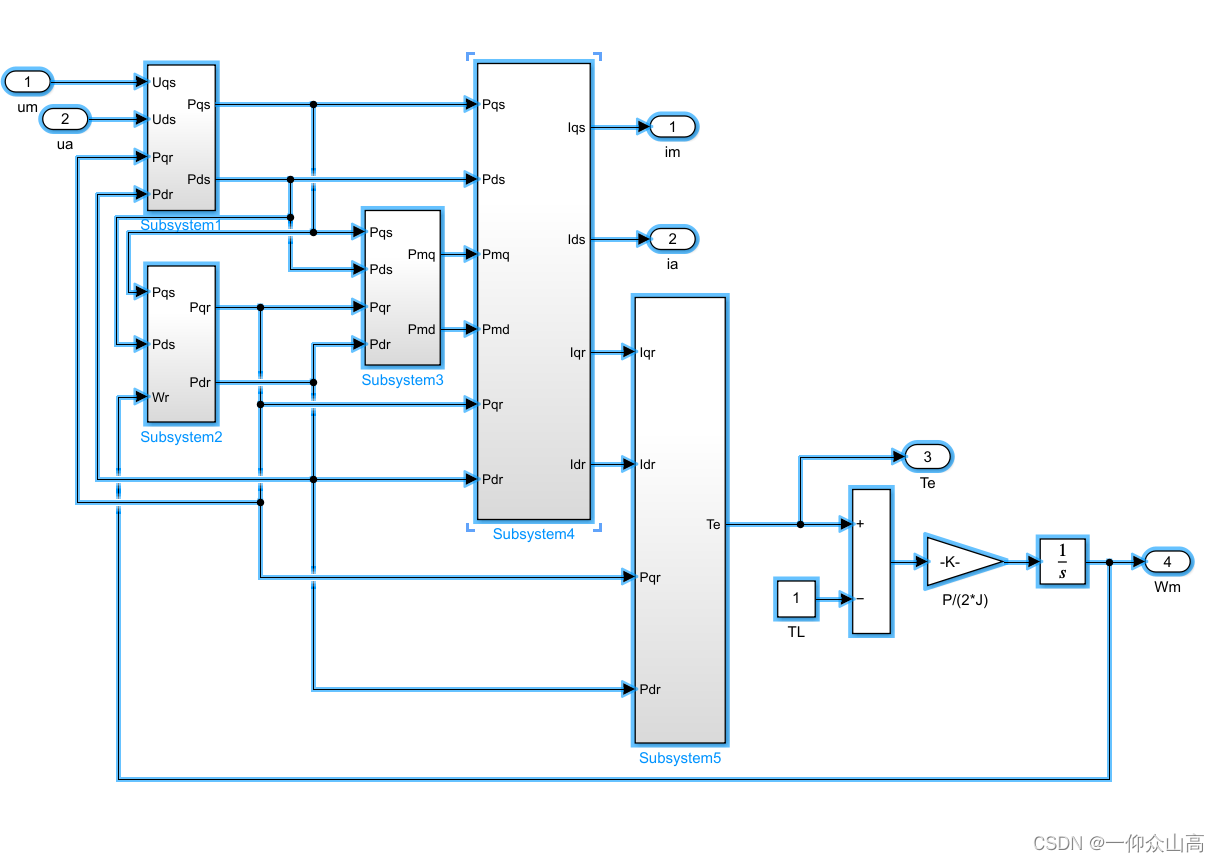
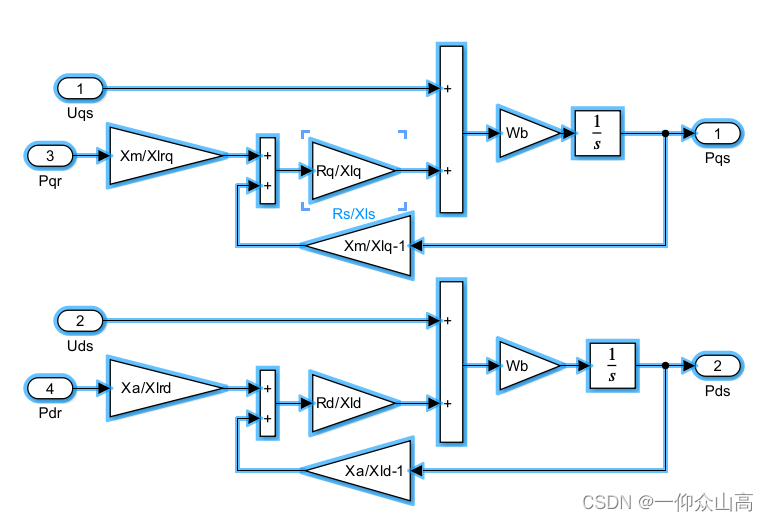
图4 子系统1的内部程序

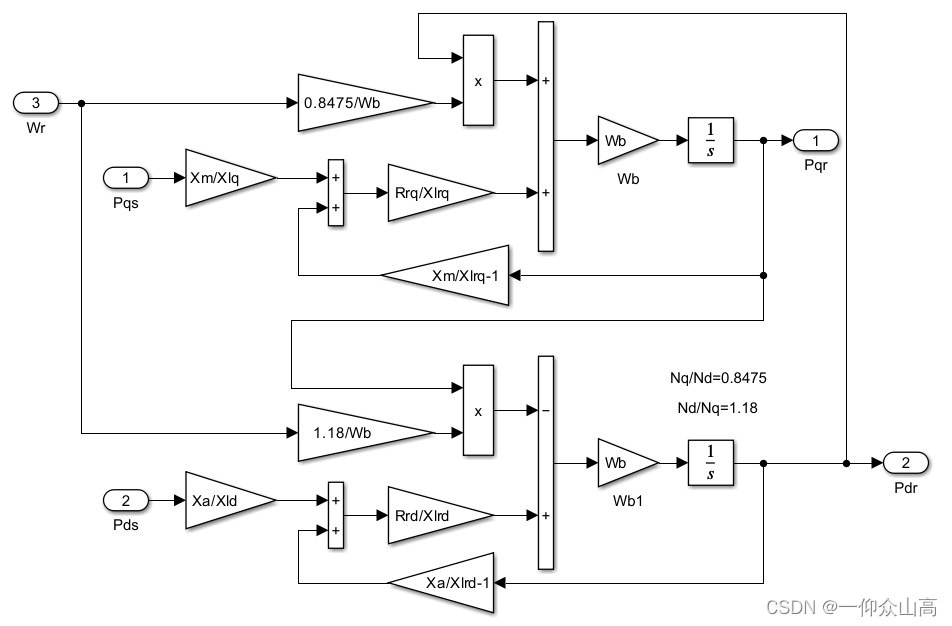
图5 子系统2的内部程序

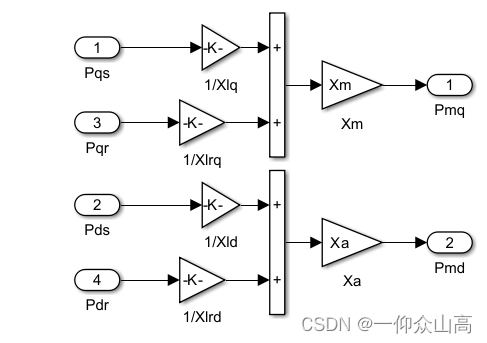
图6 子系统3的内部程序

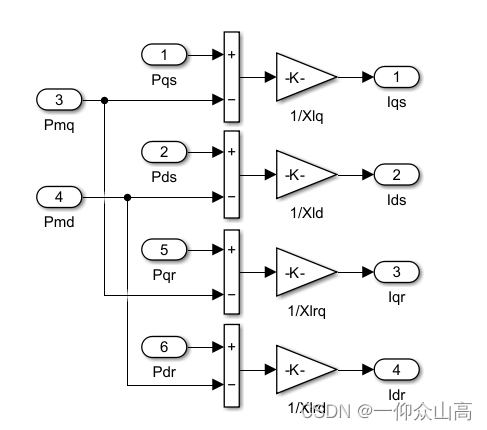
图7 子系统4的内部程序

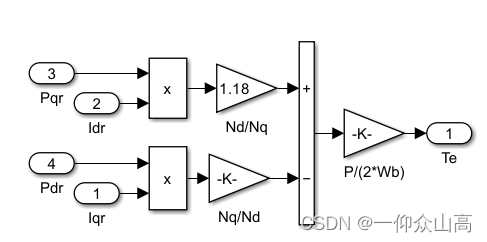
图8 子系统5的内部程序

4. 空间向量数学模型

空间向量是指在空间按正弦分布的物理量，在这里，定转子电流和定转子磁链是空间矢量，定子电压为扩展的空间矢量，J为旋转因子。设主绕组与副绕组对称，坐标轴的选取与图1相同，静止dq轴坐标系中单相感应电机的空间向量数学模型为

定子转子电压方程

$\vec{u}_{s}=R_{s}\vec{i}_{s}+p\vec{\psi}_{s}\\\vec{0}=R_{r}\vec{i}_{r}+p\vec{\psi}_{r}-\omega_{r}\vec{J}\vec{\psi}_{r}$ （7）

其中，

$\vec{u}_s=\begin{bmatrix}u_{sd}&u_{sq}\end{bmatrix}^T,\quad\vec{0}=\begin{bmatrix}0&0\end{bmatrix}^T,\quad\vec{i}_s=\begin{bmatrix}\dot{i}_{sd}&\dot{i}_{sq}\end{bmatrix}^T,\quad\vec{i}_r=\begin{bmatrix}\dot{i}_{rd}&\dot{i}_{rq}\end{bmatrix}^T$

$\vec{\psi}_s=\begin{bmatrix}\psi_{sd}&\psi_{sq}\end{bmatrix}^T,\quad\vec{\psi}_r=\begin{bmatrix}\psi_{rd}&\psi_{rq}\end{bmatrix}^T,$ $\vec{J}=\begin{bmatrix}0&1\\-1&0\end{bmatrix}$

磁链方程

$\begin{bmatrix}\psi_{sd}\\\psi_{sq}\\\psi_{rd}\\\psi_{rq}\end{bmatrix}=\begin{bmatrix}L_s&0&L_m&0\\0&L_s&0&L_m\\L_m&0&L_r&0\\0&L_m&0&L_r\end{bmatrix}\begin{bmatrix}i_{sd}\\i_{sq}\\i_{rd}\\i_{rq}\end{bmatrix}$ （8）

其中， $L_s=L_{sl}+L_m\text{,}L_r=L_{rl}+L_m$

电磁转矩方程

$T_e=n_pL_m(\vec{i}_r\otimes\vec{i}_s)$ （9）

5. 基于空间矢量数学模型的Simulink仿真模型

根据双绕组单相电容异步电动机空间矢量数学模型（方程（7）～方程（9）和转子运动方程构造的Simulink仿真模型如图9~图12所示。

图9 基于空间矢量的单相异步电动机仿真模型

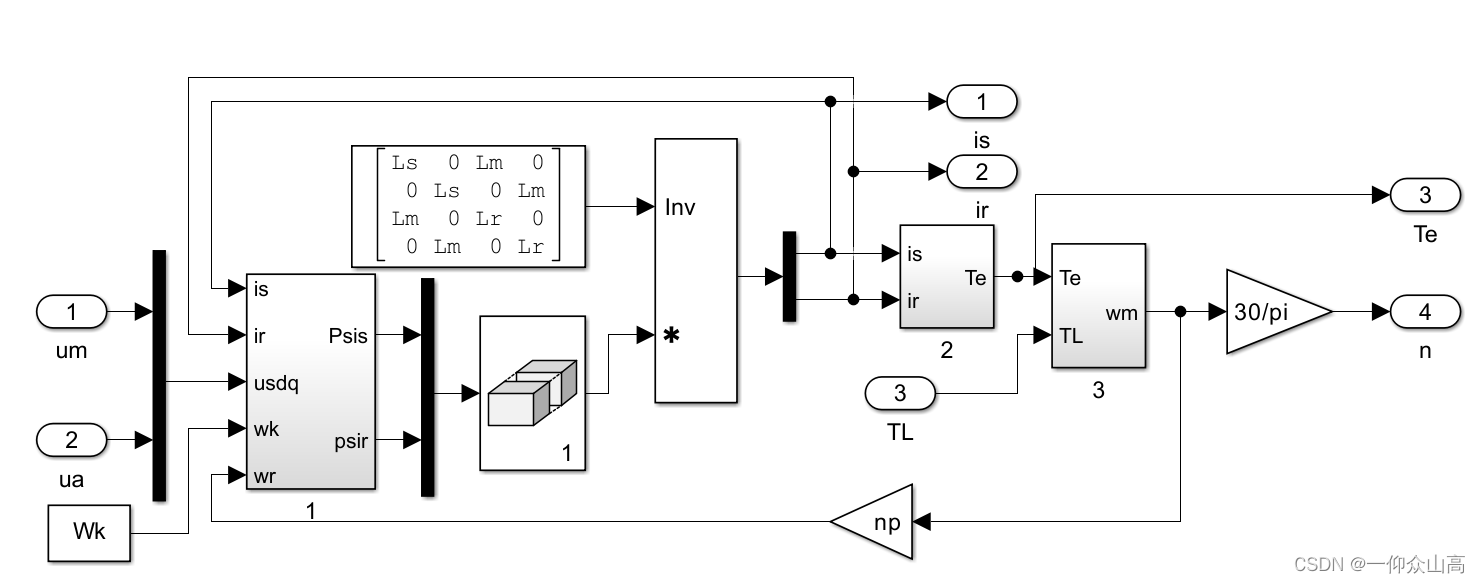
图10 图9的内部程序

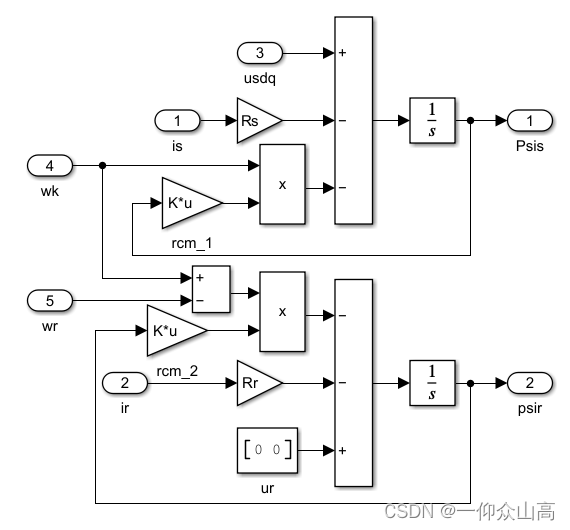
图11 图10的子系统1的内部程序（基于空间矢量的定转子电压方程）

图12 图10的子系统2的内部程序（基于电磁转矩方程）

6. 仿真实例

6.1 电源电压骤降后恢复过渡过程仿真

对单相异步电动机的电源电压骤降又重新恢复的瞬态过程进行仿真分析。仿真用的单相异步电机参数见表1，仿真模型采用基于混合磁链数学模型的Simulink仿真模型。电力系统发生三相短路故障时，继电保护装置误动作以及大容量三相电动机的切换等都有可能使电源电压瞬时骤降至正常电压的50%或更低。这里对在时间t=3s时，电源电压的幅值突然下降到60%Um，经过1s后又重新恢复到原来的额定幅值的情况进行仿真计算，仿真结果如图13和图14所示。

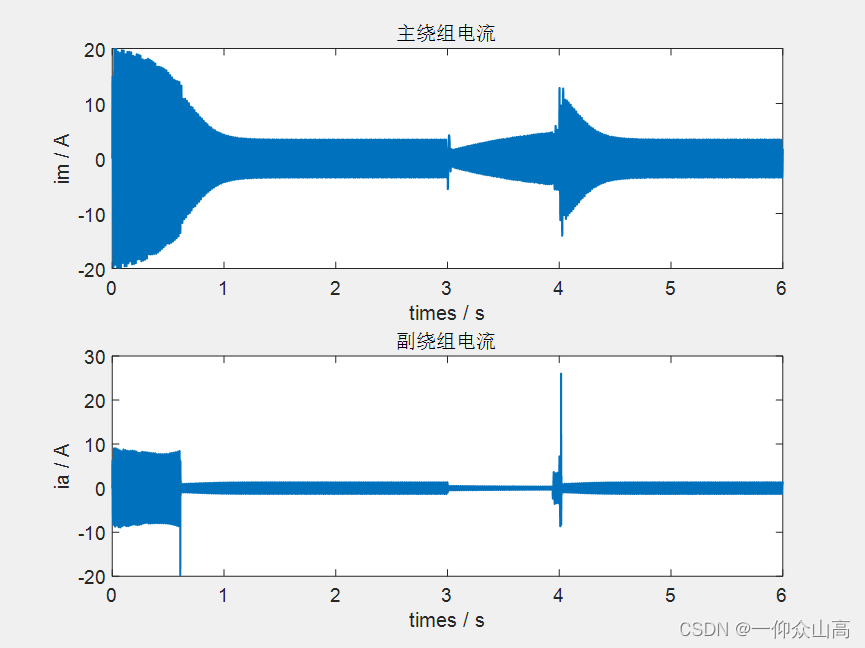
图13 电源电压骤降重新恢复的主副绕组电流波形

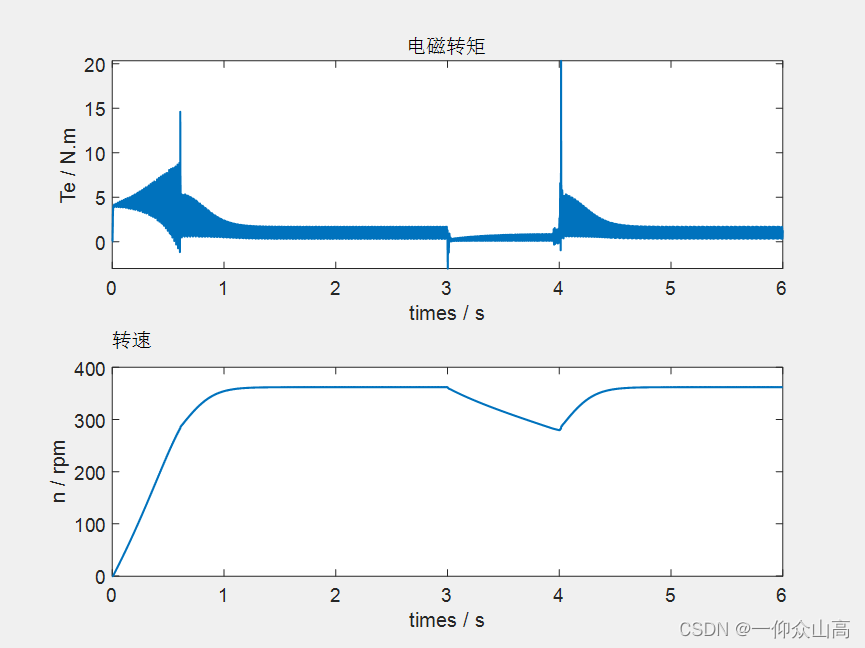
图14 电源电压骤降重新恢复的电磁转矩和转速波形

从以上仿真波形图可知，单相异步电动机运行在稳定状态，电源电压瞬时骤降时，电机将产生反向的冲击转矩，电压骤降时，由于电机的平均电磁转矩小于负载转矩，转速随之下降。当电源电压恢复瞬间，主副绕组中都产生较大的冲击电流，而副绕组的冲击电流更大。过大的冲击电流有可能引起其他电气设备跳闸，由冲击电流产生的冲击转矩有可能损坏电动机本身。

6.2 直流制动过程的仿真

单相异步电动机的直流制动，又称能耗制动，是通过将运行在电动状态的异步电机的定子主绕组脱离交流电源时，立即在绕组端通入直流励磁电流，使定子产生静止磁场。当转子由于惯性仍在旋转，其导体切割此磁场便感应电流并产生与转子转向相反的电磁制动转矩而实现制动的。这里采用基于空间矢量数学模型的Simulink仿真模型进行仿真。电机电机带阻尼性负载（n*10e-4）运行在稳定的电动状态时（t=4s)，切断交流电源，立即在绕组端施加10v直流电压，实行直流制动。仿真结果如图15~图17所示。

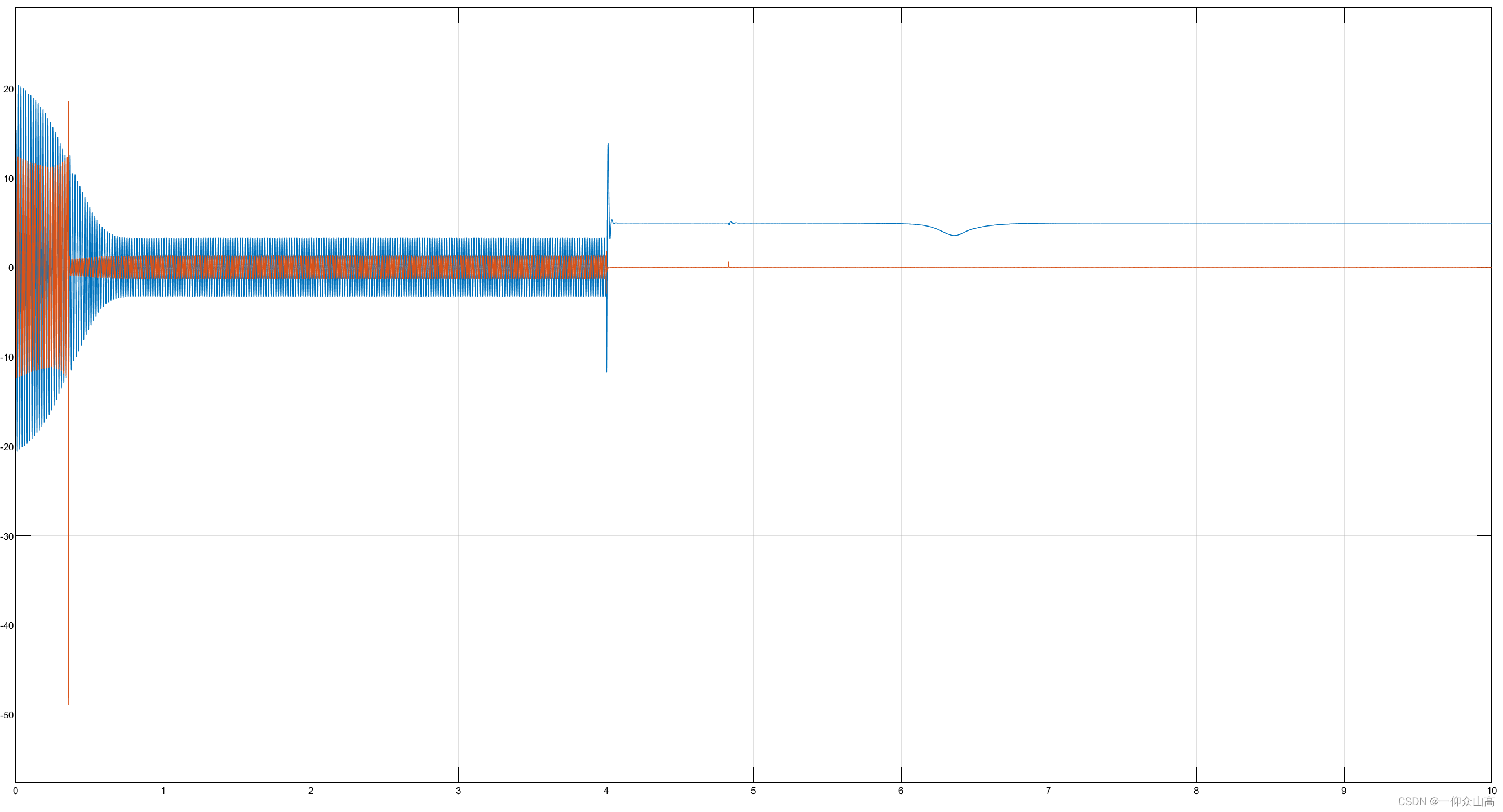
图15 直流制动过程主副绕组电流波形

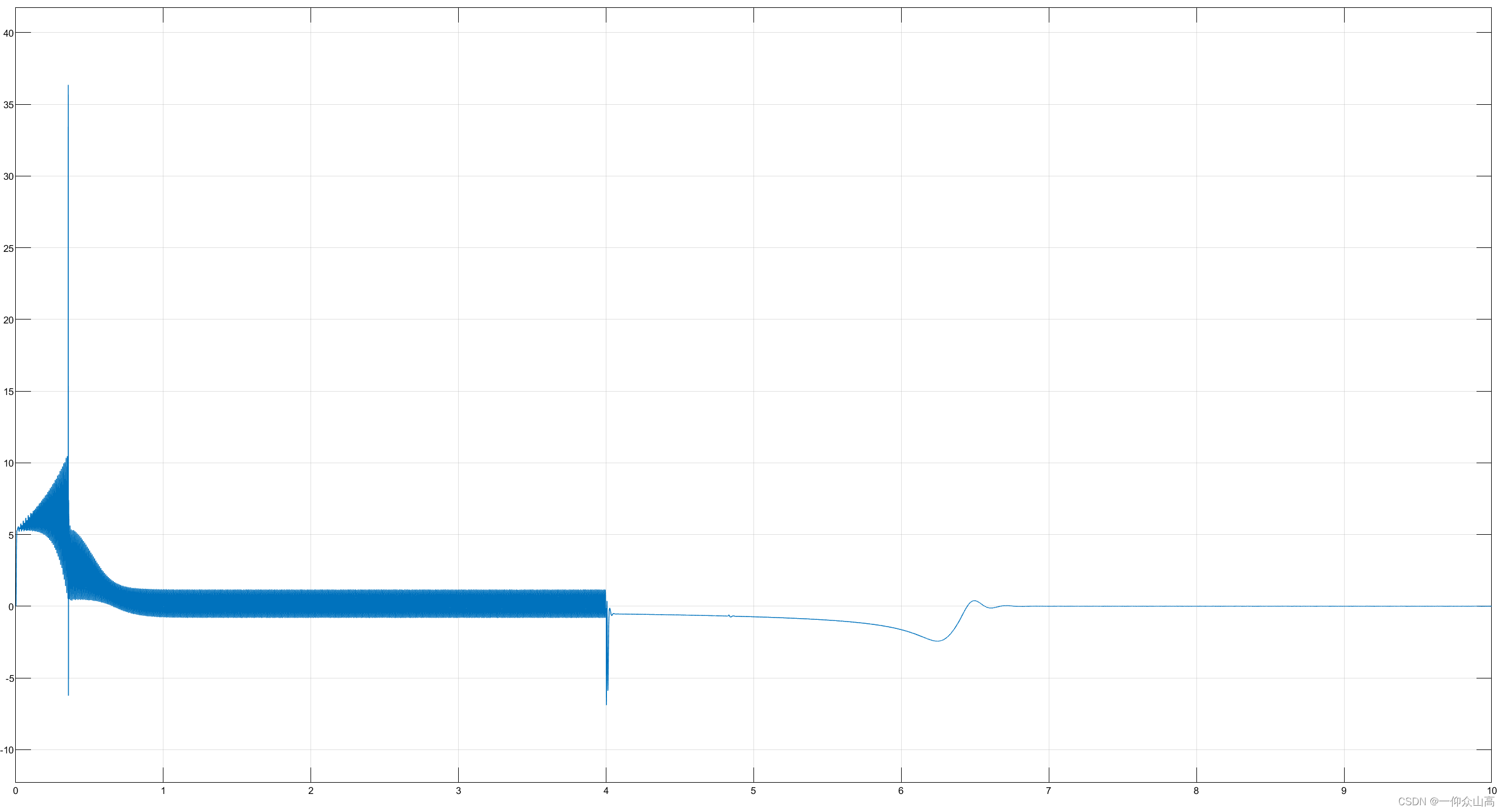
图16 直流制动过程电磁转矩波形

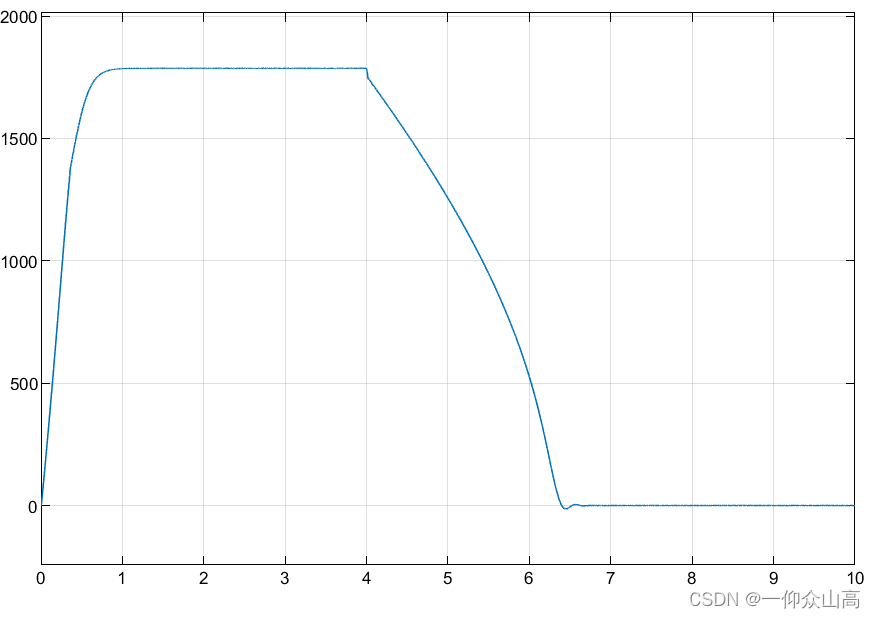
图17 直流制动过程转速波形

从图15~图17可见，直流制动时，主绕组有直流电流流过，副绕组电流为零。旋转的转子导体切割定子的直流磁场，产生与转子转向相反的电磁制动转矩，当转子转速制动到零时，电磁转矩也为零，实现准确停车。制动完毕后，应切除直流电源。

7.总结

本文根据双绕组单相电容异步电动机的混合磁链数学模型和空间矢量数学模型，用Simulink建立了它们的仿真模型，丰富了电机的建模方法。混合磁链仿真模型的稳定性要好，空间向量的仿真模型表达形式简洁，仿真速度较快。通过实例仿真验证了它们的实用性和可行性。

一仰众山高

关注

25
点赞
踩
28

收藏

觉得还不错? 一键收藏
0
评论
单相异步电动机的建模仿真（3）基于空间向量和混合磁链数学模型

不同的数学模型形式可以提供不同的视角和分析方法，这对于电机的设计、控制和故障诊断等方面具有重要意义。例如，研究以混合磁链为状态变量的数学模型并因此建立仿真模型就比以电流作为状态变量表示的数学模型和相应的仿真模型的稳定性要好，因为磁链在瞬变过程中变化相对较小，或者说较为稳定，这种模型有助于获得紧凑和稳定的瞬态过程解答。空间向量的数学模型表达形式简洁，因此器对应的simulink仿真模型也非常简洁且仿真速度较快。
复制链接

扫一扫