三相异步电动机的自耦变压器降压起动建模仿真

一仰众山高

已于 2025-02-11 23:32:38 修改

阅读量1k

点赞数 13

分类专栏：三相异步电动机各种起动方法的建模仿真文章标签：数学建模 matlab 算法软件工程

于 2025-02-06 12:29:04 首次发布

本文链接：https://blog.csdn.net/weixin_45670943/article/details/145404714

版权

三相异步电动机各种起动方法的建模仿真专栏收录该内容

4 篇文章

订阅专栏

1. 引言

2. 单相自耦变压器和三相感应电动机数学模型

3. 系统仿真模型

4. 仿真实例

5. 总结

1. 引言

三相异步电动机结构简单﹑价格低廉﹑运行可靠﹑维护方便，在工农业生产中得到了广泛应用。为使电动机能够转动起来，并很快达到工作转速，要求电动机具有足够大的电磁转矩，同时希望起动电流不要太大。起动电流大会引起电网电压下降过多，影响接在同一电网上的其它电机或电气设备的正常运行。起动转矩小使得电动机重载起动时起动困难，严重时则不能起动。

由于三相感应电动机直接起动时，起动电流通常为额定电流的4-7倍，会对电网造成较大冲击。而使用自耦变压器降压启动，可以有效降低启动电流，减少对电网的冲击。这种起动方法是利用自耦变压器降低加到电动机定子绕组的电压以减小起动电流，待转速基本稳定时再把电动机直接接到电网上。自耦变压器降压起动不受电动机绕组接线方式限制，与星-三角降压启动相比，自耦变压器降压启动的启动转矩更大，能够更好地满足电动机在启动过程中对转矩的需求。为了满足不同负载的要求，自耦变压器的二次绕组一般有三个抽头，分别为电源电压的40%﹑60%﹑80%(或55%﹑64%﹑73%)，供选择使用。该方法适合于容量较大的低压电动机，有手动和自动控制线路。其优点是电压抽头可供不同负载起动时选择，可根据允许的启动电流和所需的起动转矩选用不同的变压器电压抽头，实现灵活的起动电压调节。缺点是起动设备体积大，需要一套复杂的开关电器，价格较高，还需维护检修；自耦变压器不适用于频繁起动的场合。

三相异步电动机的起动应考虑其结构特点（是笼型还是绕线型）﹑电网的容量﹑负载的大小和性质以及机械转动惯量的高低﹑起动是否频繁等，这些是选择电动机起动方法时应该考虑的主要因素。三相异步电动机的降压起动方法很多，自耦变压器的降压起动三相异步电动机是其中之一，但是，详细全面介绍自耦变压器起动三相异步电动机建模仿真分析的文章却比较少见，本文根据自耦变压器和三相异步电动机的数学模型，建立起自耦变压器的降压起动三相异步电动机系统的仿真模型，并通过实例进行仿真，仿真结果是正确可信的。

2. 单相自耦变压器和三相感应电动机数学模型

2.1 单相自耦变压器的数学模型

自耦变压器的原边和副边之间存在直接的电气连接，所以功率是通过感应和传导从原边转移到副边的，这与双绕组变压器不同，后者的原边和副边是电气隔离的。从原理上看，单相自耦变压器可以看成由双绕组变压器演变而来。

为简单起见，建立单相自耦变压器的数学模型时作如下假定：自耦变压器的绕组绕在完全相同的铁心柱（例如环形铁心柱）上；认为整个绕组导体的材料和截面积是相同的，绕组电阻为常数，即不考虑电阻的集肤效应和温度效应。在此基础上，如果有必要，可在此数学模型的基础上加以修正，把主磁路的饱和效应和集肤效应考虑进去，建立变压器的非线性数学模型。

单相自耦变压器瞬态行为的数学模型可以写成：

$\dot{x}=Ax+Bv$ （1）

式中，

$\dot{x}=\begin{bmatrix} \frac{di_1}{dt} \\ \frac{di_2}{dt} \\ \frac{di_3}{dt} \end{bmatrix}$ ； $G=\begin{bmatrix} L_1 + L_{m1} + L_L & L_L - M & -(L_{m1} + M) \\ L_L - M & L_2 + L_{m2} + L_L & L_{m2} + M \\ -(L_{m1} + M) & L_{m2} + M & L_{m1} + L_{m2} + 2M \end{bmatrix}$ ； $x=[i_{1};1_{2};i_{3}]$ ; $A=-G^{^{-1}}\begin{bmatrix} R_1 + R_L & 0 & 0 \\ R_L & R_2 + R_L & 0 \\ 0 & 0 & R_C \end{bmatrix}$ ； $B=G^{-1}\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ 。

式（1）中，串联绕组电阻（R1）和公共绕组电阻（R2）分别是（N1-N2）匝和N2匝的电阻。同样，串联绕组的漏感（L1）和公共绕组的漏感（L2）分别是（N1-N2）匝和N2匝的漏感。因此，随着公共绕组匝数（N2）的增加，串联绕组电阻R1和电感L1减少，而公共绕组电阻R2和电感L2增加。Lm1和Lm2分别是（N1-N2）匝和N2匝的磁化电感。这种磁化电感取决于降压自耦变压器的滑环位置。M为串联绕组于公共绕组之间的互感。 $R_{c}$ 为模拟铁心损耗的电阻。

2.2 三相异步电动机的数学模型

三相感应电机在任意速dq正交坐标系中的混合磁链模型为：

$\begin{aligned} & \frac{dF_{ds}}{dt}=\omega_{b}[u_{ds}-\frac\omega{\omega_b}F_{qs}+\frac{R_{s}}{x_{ls}}(\frac{x_{ml}}{x_{lr}}F_{dr}+(\frac{x_{ml}}{x_{ls}}-1)F_{ds})]\\ & \frac{dF_{qs}}{dt}=\omega_{b}[u_{qs}-\frac\omega{\omega_b}F_{ds}+\frac{R_{s}}{x_{ls}}(\frac{x_{ml}}{x_{lr}}F_{qr}+(\frac{x_{ml}}{x_{ls}}-1)F_{qs})]\\ & \frac{dF_{dr}}{dt}=\omega_{b}[-\frac{\omega-\omega_r}{\omega_b}F_{qr}+\frac{R_r}{x_{lr}}(\frac{x_{ml}}{x_{l5}}F_{d5}+(\frac{x_{ml}}{x_{lr}}-1)F_{dr})]\\ & \frac{dF_{qr}}{dt}=\omega_{b}[\frac{\omega-\omega_r}{\omega_b}F_{dr}+\frac{R_r}{x_{lr}}(\frac{x_{ml}}{x_{ls}}F_{qs}+(\frac{x_{ml}}{x_{ls}}-1)F_{qr})]\\ & \frac{d\omega_r}{dt}=\frac{n_p}J(T_{e}-T_{L})\end{aligned}$ （2）

式中，

$T_e=1.5n_p\frac1{\omega_b}(F_{qs}i_{ds}-F_{ds}i_{qr})$ ；

$i_{ds}=\frac{1}{x_{ls}}(F_{ds}-F_{md})\\i_{qs}=\frac{1}{x_{ls}}(F_{qs}-\psi_{mq})\\i_{dr}=\frac{1}{x_{lr}}(F_{dr}-F_{md})\\i_{qr}=\frac{1}{x_{lr}}(F_{qr}-F_{mq})$

$F_{md}=x_{ml}(\frac{F_{ds}}{x_{ls}}+\frac{F_{dr}}{x_{lr}})\\F_{mq}=x_{ml}(\frac{F_{qs}}{x_{ls}}+\frac{F_{qr}}{x_{lr}})$

$x_{ml}=1/(\frac1{x_m}+\frac1{x_{ls}}+\frac1{x_{lr}})$

3.系统仿真模型

首先，建立自耦变压器的仿真模型。根据方程（1）用matlab/sinmulink的Level-2 MATLAB S-Function模块编写S函数程序，建立起单相自耦变压器的仿真模型，然后将三个一样的单相自耦变压器连接成三相组式自耦变压器，如图1所示。

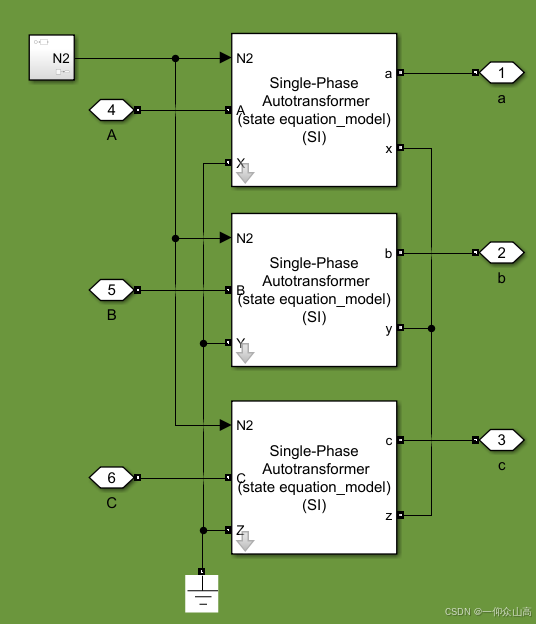
图1. 三相（组式）自耦变压器simulink仿真模型

其次，建立三相异步电动机的仿真模型。根据方程（2）用matlab/sinmulink的功能模块建立起三相异步电动机的仿真模型，如图2所示。

图2. 三相异步电动机simulink仿真模型

最后，用上面搭建的自耦变压器仿真模型和异步电动机仿真模型，根据自耦变压器起动三相异步电动机的基本要求，建立起自耦变压器降压起动三相异步电动机系统的仿真模型，如图3所示。

图3. 自耦变压器降压起动三相异步电动机仿真模型

4.仿真实例

仿真用自耦变压器额定功率为5 KVA、230 V、50 Hz、串联绕组和公共绕组总匝数N1=280匝，总电阻R=2.32欧，铁心电阻Rc=578欧，每匝磁化电感Lm0=9.7847e-6亨，总磁化电感L=0.7671亨，每匝漏感取2%L。

三相异步电动机的额定功率为2.2Kw，额定电压为380v，额定电流 $I_{N}=5.0A$ ，极对数 $p=2$ ，额定频率为50Hz，额定转速 $n_{N}=1420rpm$ ，转动惯量 $J=0.02Kg.m^{2}$ 定子绕组为 $\Delta$ 接法。每相定子电阻 $R_{1}=2.437\Omega$ ，每相转子电阻 $R_{2}=2.157\Omega$ ，每相定子漏感 $L_{ls}=7.87mH$ ，每相转子子漏感 $L_{lr}=9.529mH$ ,激磁电感 $L_{m}=270.9mH$ 。

应用图3所示的仿真模型，将上面的有关数据填入仿真模型的设置中，然后进行仿真计算。三相异步电动机带额定通风机负载。自耦变压器原边接在220v三相对称理想电源上。将自耦变压器的副边绕组匝数 $N_{2}$ 设置为三档，t=0时， $N_{2}=240$ ,t=0.4s时， $N_{2}=255$ ，t=0.8s时 $N_{2}=265$ ，t=1.4s时将自耦变压器从电网上切除，同时让三相异步电动机接在具有额定电压的电网上。仿真结果如图4所示。为便于比较，还给出了三相异步电动机直接起动时的仿真结果，如图4所示。

(a)三相异步电动机的电流波形

(b) 转速和电磁转矩曲线

图3. 自耦变压器起动三相异步电动机的瞬态特性

图4. 三相异步电动机直接起动时的电流，转速和电磁转矩曲线

从图3的仿真结果来看，起动过程中，定子绕组最大冲击电流出现在起动过程的末端，从电网切除自耦变压器时刻，最大冲击电流幅值约为20A，最大冲击直接40N.m;起动过程的前段由于电压较低，定子绕组电流较小，不到两倍额定电流，整个启动过程中，电流不超过三倍额定电流。从图4来看，异步电动机直接起动时的定子电流最大幅值约为50A，最大冲击转矩幅值约为90N.m，大大高于自耦变压器降压起动时的数值。从以上仿真结果可知，自耦变压器降压起动三相异步电动机可以有效限制起动电流，但起动时间大大增加了。

5.总结

本文根据单相自耦变压器和三相异步电动机的数学模型建立了自耦变压器降压起动三相异步电动机系统的仿真模型，通过实例仿真验证了仿真模型的正确性和实用性，为自耦变压器降压起动三相异步电动机的建模仿真提供了方法，对自耦变压器起动三相异步电动机系统的设计有实际指导意义和帮助作用。所建立的仿真模型还可以对更复杂的情况进行仿真，例如三相自耦变压器副边中性点接RC阻尼器限制副边绕组抽头切换时引起的过高的冲击电压的情况。