【卡尔曼】EKF IMU 融合算法

“在代码的海洋里，有无尽的知识等待你去发现。我就是那艘领航的船，带你乘风破浪，驶向代码的彼岸。

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

 EKF（扩展卡尔曼滤波）IMU（惯性测量单元）融合算法是一种在导航和定位系统中广泛应用的技术。 IMU 能够提供关于物体运动的加速度和角速度等信息，但由于测量误差的累积，单独使用 IMU 进行长时间的定位和导航会导致较大的偏差。 EKF 则是一种有效的状态估计方法，它能够融合来自多个传感器的测量数据，以降低不确定性和误差。 在 EKF IMU 融合算法中，将 IMU 的测量值与其他传感器（如 GPS、视觉传感器等）的测量值相结合。通过建立系统的数学模型，EKF 对 IMU 的测量误差进行估计和修正，从而得到更准确和可靠的状态估计，包括位置、速度和姿态等。 这种融合算法在机器人导航、自动驾驶、航空航天等领域发挥着重要作用，能够提高系统的精度、稳定性和可靠性。

📚2 运行结果

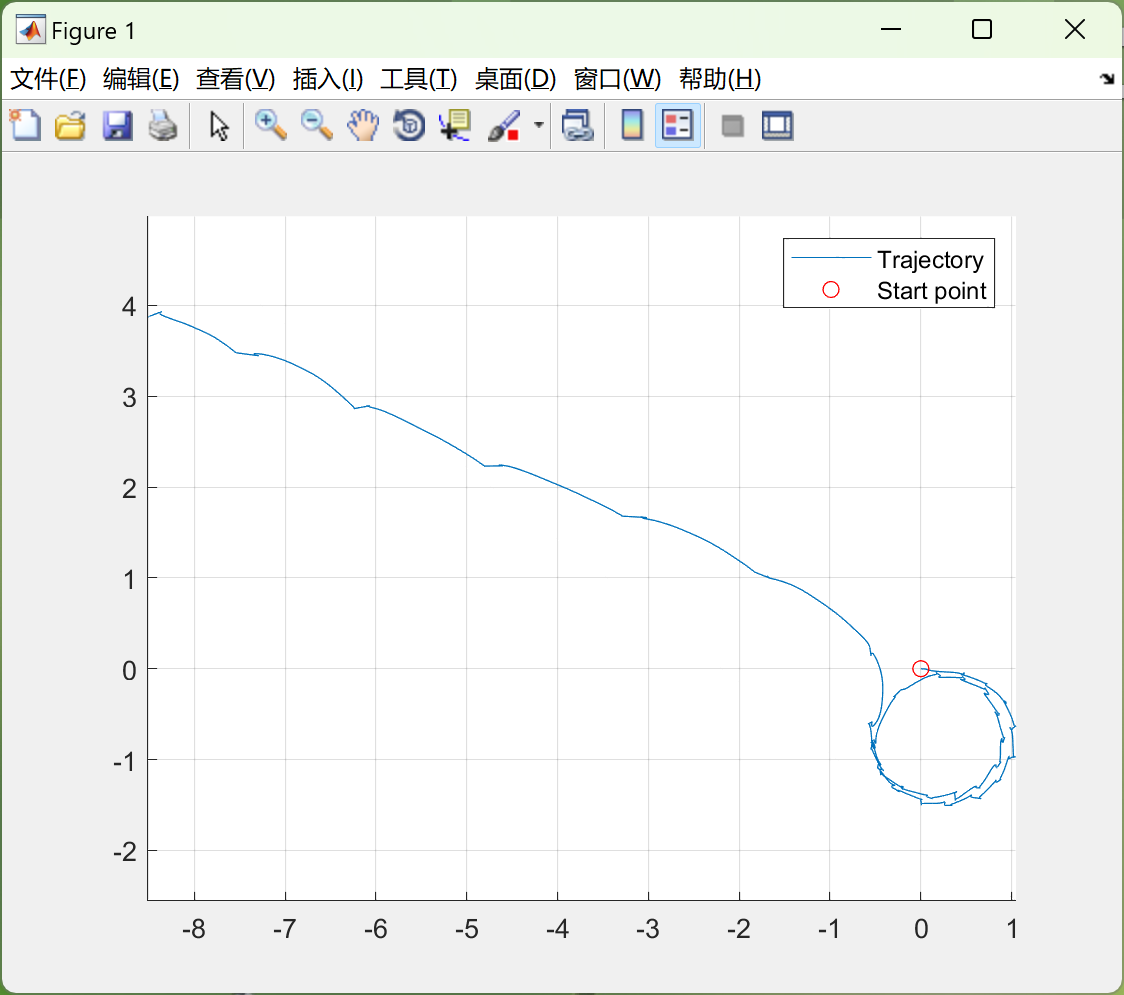
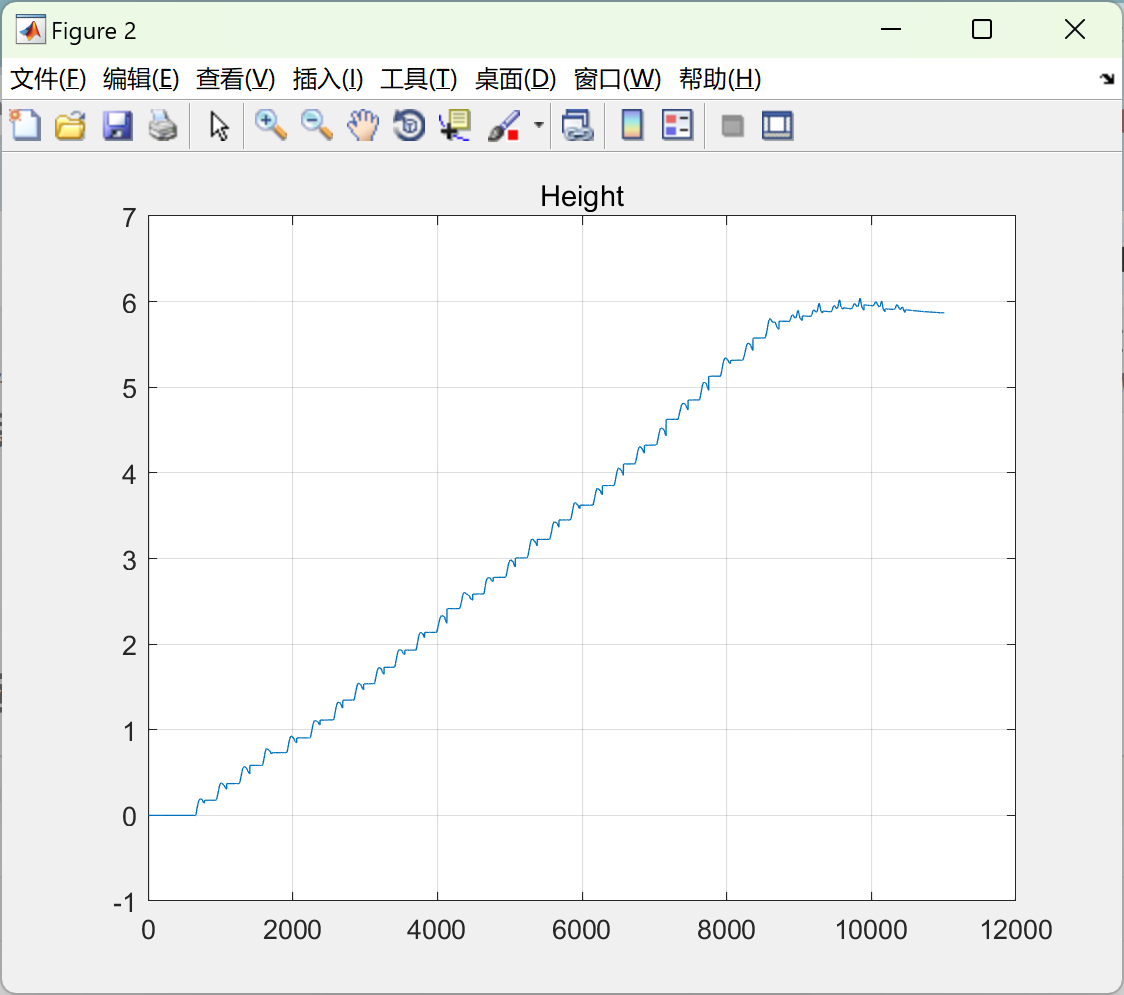
主函数部分代码：

clear; close all; clc;

%--- Dataset parameters
deltat = 1/200;             % Sampling period
noise_gyro = 2.4e-3;        % Gyroscope noise(discrete), rad/s
noise_accel = 2.83e-2;      % Accelerometer noise, m/s^2
gravity = 9.81007;          % Gravity magnitude, m/s^2

%--- Load data
% Each row of IMU data : 
% (timestamp, wx, wy, wz, ax, ay, az)
% Each row of Ground truth data : 
% (time, position, quaternion, velocity, gyroscope bias, accelerometer bias)
data = load('data/attitude_data.mat');
imu_data = data.imu_data;   % IMU readings
grt_data = data.grt_data;   % Ground truth (GT)
grt_q = grt_data(:, 5:8);   % GT quaternions

bias_w = grt_data(1, 12:14);    % gyroscope bias
bias_a = grt_data(1, 15:17);    % accelerometer bias


%--- Container of the results
N = length(imu_data);
allX = zeros(N, 4);


%--- Initialization
x = grt_q(1,:)';            % Initial state (quaternion)
P = 1e-10 * eye(4);         % Initial covariance
allX(1,:) = x';


% ---Here we go !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
for k = 2 : N
    
    %--- 1. Propagation --------------------------
    % Gyroscope measurements
    w = (imu_data(k-1, 2:4) + imu_data(k, 2:4))/2;
    w = w - bias_w;
    

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]陈徵粼,刘灏,毕天姝.基于配电网PMU的无监督电力系统扰动特征提取与分类[J/OL].中国电机工程学报:1-13[2024-01-10].https://doi.org/10.13334/j.0258-8013.pcsee.230464.

[2]刘泳,陈帝伊,张猛等.水电煤电协同发展促进电力系统低碳转型方案评价[J/OL].人民长江:1-11[2024-01-10].http://kns.cnki.net/kcms/detail/42.1202.tv.20240108.1403.004.html.

🌈4 Matlab代码实现