二维多孔介质图像的粒度分布研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

二维多孔介质图像的粒度分布研究

1. 引言

2. 二维多孔介质的定义与结构类型

3. 粒度分布研究方法

3.1 图像获取与预处理

3.2 图像分割算法

3.3 孔隙特征提取与粒度定义

3.4 粒度分布计算

4. 测量标准与方法的对比

5. 统计分析方法的应用

6. 机器学习建模案例

7. 挑战与文献综述

8. 未来发展方向

结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

二维多孔介质图像的粒度分布研究

使用流域分割算法对岩石二维二值图像进行粒度分布的研究是一项重要的任务。粒度分布是指岩石样本中不同颗粒大小的分布情况，对于了解岩石的物理性质和工程行为具有重要意义。

在进行粒度分布研究时，首先需要获取岩石的二维二值图像。这可以通过采用现代高分辨率成像技术，如扫描电子显微镜（SEM）或计算机断层扫描（CT）等方法来实现。然后，使用流域分割算法对图像进行处理，将图像划分为不同的流域或区域，以便对每个区域的粒度进行分析。

流域分割算法是一种基于图像处理和计算机视觉技术的方法，可以将图像中的像素分成不同的区域，使得每个区域具有相似的特征。在岩石图像中，流域分割算法可以将不同类型的颗粒或孔隙分离出来，从而实现对不同颗粒大小的分析。

通过对每个流域或区域进行粒度分析，可以得到岩石样本中不同颗粒大小的分布情况。这可以通过计算每个区域中颗粒的面积或周长来实现。此外，还可以通过计算每个区域中颗粒的等效直径或体积来获得更详细的粒度信息。

粒度分布的研究对于岩石的物理性质和工程行为有着重要的影响。不同颗粒大小的分布情况可以反映岩石的孔隙结构、渗透性和强度等特性。例如，颗粒较大的区域通常具有较高的渗透性，而颗粒较小的区域则可能具有较高的强度。因此，通过粒度分布的研究，可以为岩石的工程设计和地质勘探提供重要的参考依据。

1. 引言

多孔介质的微观孔隙结构直接影响其宏观物理化学性质（如渗透性、吸附性等），而孔隙粒度分布（Pore Size Distribution, PSD）是描述孔隙空间特征的核心参数之一。传统方法（如压汞法、气体吸附法）存在破坏性且难以捕捉真实孔隙形貌，而基于二维图像的粒度分析因其非破坏性和高信息密度成为重要研究手段。本文将从定义、方法、挑战及未来方向系统阐述该领域的研究进展。

---

2. 二维多孔介质的定义与结构类型

二维多孔介质图像是通过显微成像技术（如SEM、CT）获取的二维切片，呈现孔隙与固相骨架的空间分布。其结构类型多样，包括：

• 蜂窝状结构：大孔洞通过狭窄通道连接，常见于滤材。

  

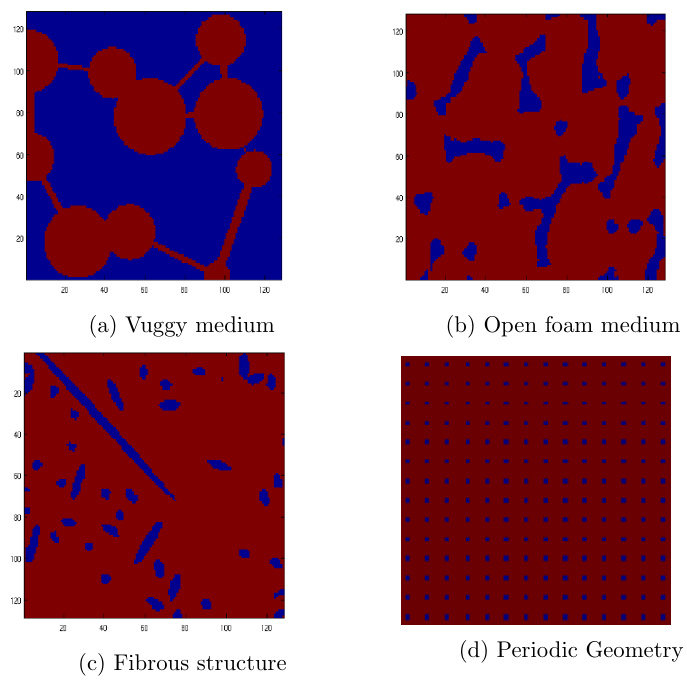
• 纤维状结构：细长纤维交织形成开放网络，影响流体渗透路径。
• 周期性几何结构：均匀排列的正方形网格，用于简化模型研究。
  不同结构的多孔介质在渗透性、孔隙连通性等方面差异显著，需针对性分析其粒度分布。

---

3. 粒度分布研究方法

基于二维图像的粒度分析流程包括以下关键步骤：

3.1 图像获取与预处理

• 成像技术：SEM（纳米级分辨率）、X射线CT（三维重建基础）、光学显微镜（宏观结构）等。
• 预处理：滤波（高斯滤波去噪）、灰度校正、对比度增强，以优化分割效果。

3.2 图像分割算法

• 阈值法：Otsu算法自动选择阈值，适用于灰度分布均匀的图像。
• 分水岭算法：通过距离变换识别孔隙中心，易过度分割，需结合标记控制。
• SNOW算法：改进分水岭法，通过高斯滤波和峰值修剪解决高孔隙率材料的过度分割问题，显著提升孔隙网络提取精度。
• 机器学习方法：U-Net等深度学习模型在复杂孔隙分割中表现优异，尤其适用于噪声大或边界模糊的图像。

3.3 孔隙特征提取与粒度定义

• 等效直径：将孔隙面积等效为圆形直径，计算简单但忽略形状复杂性。
• 最大内切圆直径：反映孔隙的“最小通道”尺寸，对渗透性研究更具意义。
• 骨架化分析：提取孔隙中轴线，量化分支长度与曲折度，适用于连通性评估。

3.4 粒度分布计算

• 统计方法：以孔隙尺寸为横坐标，数量/面积占比为纵坐标绘制直方图或累积曲线。
• 分形维数：通过计盒法或面积-周长关系计算，表征孔隙分布的自相似性（如煤岩分形维数D≈1.6–1.8）。

---

4. 测量标准与方法的对比

• 传统方法：

  方法	原理	局限性
  压汞法	高压注入汞测量孔径	破坏样品，仅测开孔
  气体吸附法	气体吸附等温线计算比表面积	无法获取形态信息
  激光衍射	散射光模式反演粒径	依赖球形假设，误差较大

• 图像分析法优势：非破坏性、可结合形态学参数（如长宽比、迂曲度），但需解决二维到三维的推断误差。

---

5. 统计分析方法的应用

• 孔隙率计算：通过二值化图像统计孔隙像素占比，公式为 ϕ=Vp/Vb×100%ϕ=Vp​/Vb​×100%，误差可控制在±2%以内。
• 分形分析案例：煤岩SEM图像经二值化后，分形维数 DfDf​ 通过 lg⁡N(k)∝−Dflg⁡klgN(k)∝−Df​lgk 计算，揭示孔隙复杂度与渗透性的关联。
• 局部孔隙率分布：通过滑动窗口统计局部孔隙率，生成直方图以反映空间异质性。

---

6. 机器学习建模案例

• 图像分割：基于卷积神经网络（CNN）的U-Net模型在岩心FIB-SEM图像中实现孔隙与矿物的高精度分割，准确率达92%。
• 三维重建：使用生成对抗网络（GAN）从二维切片预测三维孔隙结构，减少对高成本CT扫描的依赖。
• 渗透性预测：结合孔隙网络模型与随机森林算法，输入孔隙尺寸、连通性等特征，预测渗透率的误差小于10%。

---

7. 挑战与文献综述

• 二维局限性：切面效应导致小孔隙漏检，如纤维介质中切面可能低估30%的孔隙尺寸。
• 多孔介质异质性：松散砂土中粒度分布与渗透率呈非线性关系，需结合分形维数修正模型。
• 动态过程模拟：晶格玻尔兹曼方法（LBM）揭示胶体颗粒在孔隙中的堵塞机制，渗透率下降可达50%。

---

8. 未来发展方向

1. 高分辨率成像：发展亚纳米级SEM和同步辐射CT技术，捕捉微孔隙细节。
2. AI驱动分析：结合迁移学习与少样本训练，提升复杂介质的分割效率。
3. 多尺度融合：整合宏观CT与微观SEM数据，建立跨尺度孔隙网络模型。
4. 标准化与验证：推动图像分析法与传统测量（如BET）的交叉验证，制定行业标准。

---

结论

二维多孔介质图像的粒度分布研究通过结合图像处理、统计分析与机器学习，为材料设计、油气开采等领域提供了微观结构解析工具。尽管存在维度转换和异质性挑战，随着成像与算法的进步，其精度和应用范围将持续扩展，成为多孔介质研究不可或缺的技术支柱。

📚2 运行结果

部分代码：

%Outputs
Average_grain_radius_micron=mean(R)
Standard_deviation_of_grain_radius_micron=std(R)
figure('units','normalized','outerposition',[0 0 1 1])
subplot(1,2,1)
RGB=label2rgb(Pr_L,'jet', 'w', 'shuffle');
imshow(RGB)
imwrite(RGB,'Output.png')

subplot(1,2,2)
Rel_Frequencies=hist(R,[1:round(max(R)/Bins):round(max(R))])./sum(sum(hist(R,[1:round(max(R)/Bins):round(max(R))]))); 
bar([1:round(max(R)/Bins):round(max(R))],Rel_Frequencies); 
xlabel('Equivalent Grain Radius (micron)'); ylabel('Relative Frequency'); axis([1 max(R) 0 max(Rel_Frequencies)]); axis square;
annotation('textbox',[.2 .85 .1 .1], 'String', [ 'Average grain radius = ' num2str(Average_grain_radius_micron) ' micron'])

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]Rabbani, A., Ayatollahi, S. (2015). Comparing three image processing algorithms
to estimate the grain-size distribution of porous rocks from binary 2d images and
sensitivity analysis of the grain overlapping degree. Special Topics & Reviews in
Porous Media: An International Journal 6 (1), 71-89.

🌈4 Matlab代码实现