中尺度混凝土二维有限元求解——运行弯曲、运行光盘、运行比较、运行半圆形（Matlab代码实现）

最新推荐文章于 2025-05-14 22:44:21 发布

荔枝科研社

最新推荐文章于 2025-05-14 22:44:21 发布

阅读量925

点赞数 19

文章标签： matlab 算法人工智能

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147921025

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

中尺度混凝土二维有限元求解研究

一、中尺度混凝土模型构建与二维有限元方法结合

二、运行弯曲（Bending Analysis）的有限元实现

三、运行光盘（Case Study with CD/DVD Data）

四、运行比较（Result Comparison Methodology）

五、半圆形结构研究文档要点

六、总结与建议

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

中尺度混凝土二维有限元求解研究

中尺度混凝土二维有限元求解是一种常见的工程分析方法，用于研究混凝土结构在运行条件下的行为。在这种方法中，混凝土结构被建模为一个二维平面，通过有限元分析求解结构的应力和变形。

在运行弯曲研究中，我们主要关注混凝土梁或板在加载条件下的弯曲响应。通过应用适当的边界条件和加载条件，可以计算出结构的应力和变形分布。这对于设计和评估混凝土梁和板的性能非常重要。

在运行光盘研究中，我们主要关注混凝土盘的行为。这种结构常见于圆形或环形的平台、桥梁和水池等工程中。通过分析结构的应力和变形，可以评估其在运行条件下的稳定性和安全性。

在运行比较研究中，我们可以比较不同类型的混凝土结构，在相同的加载条件下的行为差异。这可以帮助我们选择最合适的结构形式和材料，以满足设计要求和性能需求。

在运行半圆形研究中，我们主要关注半圆形结构的行为。这种结构常见于隧道、拱桥和圆形水池等工程中。通过分析结构的应力和变形，可以评估其在运行条件下的稳定性和安全性。

一、中尺度混凝土模型构建与二维有限元方法结合

中尺度混凝土的定义与特点
中尺度模型将混凝土视为由骨料、砂浆及界面过渡区（ITZ）组成的多相复合材料。其核心优势在于能捕捉微裂纹萌生、扩展及局部化变形，而均质化模型无法实现。二维模型中，骨料通常采用随机分布的凸多边形或圆形颗粒，体积分数控制在30%-50%，ITZ通过等厚度粘结单元或零厚度界面单元表示，避免直接网格化的困难。
二维有限元实现的关键技术
- 几何生成：采用蒙特卡洛算法或“网格-放置-识别-分配”（MPIA）程序生成随机骨料结构。例如，中通过随机放置不同尺寸的骨料，确保不相交并满足粒径分布要求。
- 材料属性分配：砂浆和骨料的本构模型常选择弹性损伤模型或RHT模型，ITZ的强度通常低于砂浆。材料异质性可通过威布尔分布函数和空间相关系数表征。
- 网格划分：骨料采用四面体或三角形单元，ITZ区域使用高长宽比界面单元。对于半圆形等特殊几何，需在曲率变化处加密网格。
- 损伤模拟：扩展有限元法（XFEM）或粘聚单元法用于裂纹扩展模拟，如中通过模糊裂纹模型实现软化行为分析。
典型应用场景
- 单轴拉伸/压缩：揭示砂浆强度对混凝土整体强度的主导作用，ITZ弱化导致裂纹沿界面扩展。
- 动态加载：考虑率效应时，需引入动态本构关系（如黏弹性模型）。
- 复杂几何分析：半圆形结构（如拱形构件）的稳定性分析需结合对称边界条件和初始缺陷模拟。

二、运行弯曲（Bending Analysis）的有限元实现

弯曲工况定义
弯曲分析模拟结构在弯矩作用下的变形与失效，常见于梁、板构件。中尺度模型中需考虑骨料分布对中性轴偏移的影响。
关键设置步骤
- 边界条件：对称结构可采用1/2或1/4模型，两端施加简支或固支约束。
- 载荷施加：通过节点力或位移加载实现弯矩分布，如中通过旋转集中力模拟动态弯矩。
- 失效判据：基于最大主应力、应变能释放率或损伤变量（如中通过塑性损伤模型判断屈曲）。
典型案例
- 车架弯曲：中通过施加动态载荷因子（≤2.5倍静载）验证强度。
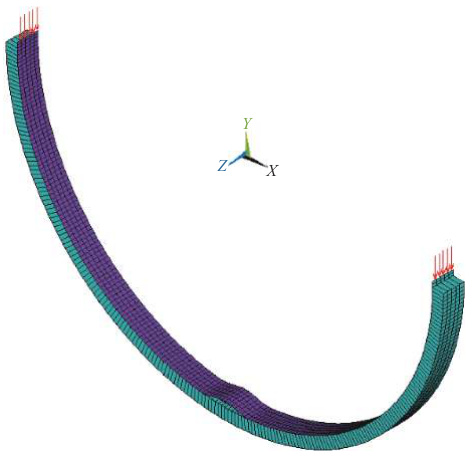
- 钢拱稳定性：中半圆形钢拱的非弹性屈曲分析，对比试验与有限元结果误差在5%以内。

三、运行光盘（Case Study with CD/DVD Data）

光盘内容与用途
光盘通常包含预定义模型文件（.inp、.db）、材料库及命令流脚本。例如，中提供30个算例，涵盖网格划分、边界条件设置及后处理模板。
操作流程
- 模型导入：通过ANSYS Workbench直接加载几何文件，或使用命令流（如中/INPUT命令）。
- 参数修改：调整骨料体积分数、ITZ厚度等中尺度参数。
- 结果提取：利用内置脚本自动输出应力云图、裂纹路径及载荷-位移曲线。
示例应用
- 混凝土梁开裂模拟：调用预制模型研究不同骨料形状（圆形vs多边形）对裂纹模式的影响。
- 动态冲击分析：通过Y2D程序模拟混凝土柱的轴向冲击破碎过程。

四、运行比较（Result Comparison Methodology）

对比维度
- 实验验证：将模拟应力-应变曲线、裂纹形态与试验数据对比（如中单轴压缩模拟误差<10%）。
- 方法对比：有限元与离散元（FEM vs DEM）、晶格模型等的计算效率与精度差异。
- 参数敏感性：分析砂浆强度、骨料尺寸等对结果的贡献度。
误差控制策略
- 网格收敛性：通过细化网格直至相邻两次计算差异<5%。
- 对称性检查：确保对称结构的网格和应力分布对称。
- 能量平衡：验证外力功与内能、损伤耗散的一致性。
工具与可视化
- 后处理软件：使用ParaView或GiD生成对比图表。
- 自动化脚本：编写Python或APDL脚本批量处理多组数据。

五、半圆形结构研究文档要点

几何建模
- 网格划分：曲率半径处采用过渡单元（如图36中半圆板的分层细化）。
- 边界条件：对称轴施加位移约束，载荷施加于拱顶。
特殊问题处理
- 初始缺陷：引入几何偏差（如0.1%跨度）模拟实际制造误差。
- 动态响应：半圆形拱在冲击载荷下的屈曲模态分析。
典型案例
- 钢拱稳定性：中通过试验校正有限元模型，预测非弹性屈曲载荷与实测值偏差<8%。
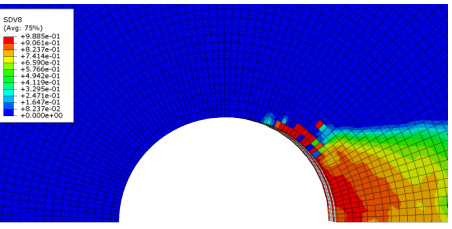
- 复合材料压力容器：图35中半圆环的损伤演化模拟，预测初始凹陷区域的应力集中系数。

六、总结与建议

中尺度模型优势：揭示材料异质性对宏观力学行为的影响，适用于断裂、动态加载等复杂场景。
二维分析局限：无法完全反映三维应力状态，需通过平面应变/应力假设简化。
未来方向：结合机器学习优化骨料分布，开发GPU并行计算提升效率。

通过上述方法，用户可系统构建中尺度混凝土二维有限元模型，并针对弯曲、半圆形结构等场景开展深入研究。

📚2 运行结果

部分代码：

Plot_Results(Job1{end}.Model,Show_Deformed,Mag_Factor,Result_type1);
legend('Isotropic Damage');

Plot_Results(Job2{end}.Model,Show_Deformed,Mag_Factor,Result_type2);
legend('Normal Crack Strain');

for i=1:1:length(Job1)

Load1(i)=0;

for j=1:1:M1
Load1(i)=Load1(i)+Job1{i}.Model.Constraint{j}.F;
end

Displacement1(i)=Job1{i}.Model.Constraint{1}.U;

end

for i=1:1:length(Job2)

Load2(i)=0;

for j=1:1:M1
Load2(i)=Load2(i)+Job2{i}.Model.Constraint{j}.F;
end

Displacement2(i)=Job2{i}.Model.Constraint{1}.U;

end

figure;

plot([0 Displacement1],[0 Load1],'b-',[0 Displacement2],[0 Load2],'r--');
legend('Isotropic Damage Model','Fixed Crack Model');
xlabel('Displacement(mm)');
ylabel('Load (N)');

xlabel('Displacement(mm)');
ylabel('Force Norm');