一.域F上线性空间的同构(8.3)

1.线性空间同构
(1)定义:


(2)同构映射的性质:
性质1: σ ( 0 ) σ(0) σ(0)是 V ′ V' V′的零元 0 ′ 0' 0′
性质2:对于∀ α ∈ V α∈V α∈V,有 σ ( − α ) = − σ ( α ) σ(-α)=-σ(α) σ(−α)=−σ(α)
性质3:对V中任一向量组 α 1 . . . α s α_1...α_s α1...αs,F中任意1组元素 k 1 . . . k s k_1...k_s k1...ks,有 σ ( k 1 α 1 + . . . + k s α s ) = k 1 σ ( α 1 ) + . . . + k s σ ( α s ) σ(k_1α_1+...+k_sα_s)=k_1σ(α_1)+...+k_sσ(α_s) σ(k1α1+...+ksαs)=k1σ(α1)+...+ksσ(αs)
性质4:V中的向量组 α 1 . . . α s α_1...α_s α1...αs线性相关当且仅当 σ ( α 1 ) . . . σ ( α s ) σ(α_1)...σ(α_s) σ(α1)...σ(αs)是V’中线性相关的向量组
性质5:如果 α 1 . . . α n α_1...α_n α1...αn是V的1个基,则 σ ( α 1 ) . . . σ ( α n ) σ(α_1)...σ(α_n) σ(α1)...σ(αn)是V’的1个基
性质6:若 σ σ σ是 V V V到 V ′ V' V′的1个同构映射,则 σ σ σ是 V V V到 V ′ V' V′的1个可逆的线性映射
(3)同构的判定:
定理1:域F上2个有限维线性空间同构的充要条件是:这2个线性空间的维数相等
推论1:若 σ σ σ是V到V’的1个同构映射,则V中向量 α α α在基 α 1 . . . α n α_1...α_n α1...αn下的坐标 ( a 1 . . . a n ) ′ (a_1...a_n)' (a1...an)′也是V’中向量 σ ( α ) σ(α) σ(α)在基 σ ( α 1 ) . . . σ ( α n ) σ(α_1)...σ(α_n) σ(α1)...σ(αn)下的坐标
(4)子空间的同构:
命题1:设 σ σ σ是域F上线性空间V到V’的1个同构映射,如果U是V的1个子空间,则 σ ( U ) σ(U) σ(U)是V’的1个子空间;如果U是有限维的,则 σ ( U ) σ(U) σ(U)也是有限维的,且 d i m σ ( U ) = d i m U dim\,σ(U)=dim\,U dimσ(U)=dimU
(5)同构类:
所有同构类组成的集合是数域 K K K上所有线性空间组成的集合 Ω Ω Ω的1个划分
限制到所有有限维线性空间组成的集合S上,所有同构类组成的集合也是 S S S的1个划分
2.有限域的元素个数:
定理2:设 F F F是任一有限域,则 F F F的元素个数是1个素数 p p p的方幂,其中 p p p是 F F F的特征
3.线性空间的外直和
(1)概念:

(2)维数:
定理3:设 U , W U,W U,W是域 F F F上的2个线性空间,则 U + ˙ W U\dot{+}W U+˙W是其2个子空间 U + ˙ 0 , 0 + ˙ W U\dot{+}0,0\dot{+}W U+˙0,0+˙W的直和,其中 U + ˙ 0 ≅ U , 0 + ˙ W ≅ W U\dot{+}0\cong U,0\dot{+}W\cong W U+˙0≅U,0+˙W≅W.如果 U , W U,W U,W都是域 F F F上的有限维线性空间,则 dim ( U + ˙ W ) = dim U + dim W \dim(U\dot{+}W)=\dim{U}+\dim{W} dim(U+˙W)=dimU+dimW
(3)多个线性空间的外直和:

二.商空间(8.4)

集合 V V V对于等价关系 R R R的划分也称为 V V V对于 R R R的商集,记为 V / R V/R V/R或 V R V_R VR
1.商空间
(1)商空间的概念:




注意:商空间 V / W V/W V/W的1个元素是 V V V的1个等价类,而不是 V V V中的1个向量
(2)商空间的维数:
定理4:设 V V V是域 F F F上的1个有限维线性空间, W W W是 V V V的1个子空间,则 d i m ( V / W ) = d i m V − d i m W ( 8 ) dim(V/W)=dim\,V-dim\,W\qquad(8) dim(V/W)=dimV−dimW(8)
(3)商空间与补空间:
定理5:如果商空间 V / W V/W V/W的1个基为 β 1 + W , β 2 + W , . . . , β t + W β_1+W,β_2+W,...,β_t+W β1+W,β2+W,...,βt+W,令 U = < β 1 , β 2 . . . β t > U=<β_1,β_2...β_t> U=<β1,β2...βt>,则 V = W ⊕ U V=W\oplus U V=W⊕U,即 U U U是 W W W的补空间,且 β 1 , β 2 . . . β t β_1,β_2...β_t β1,β2...βt是 U U U的1个基
注意:这里的 V V V和 W W W都可以是无限维的,但要求 V / W V/W V/W和 U U U是有限维的
因此,无限维的子空间 W W W也具有补空间,从而域 F F F上线性空间 V V V的任一子空间都有补空间
这是对 线性空间.线性空间与子空间.二.3.(3) 部分命题3的推广
更进一步的推广见 二.3.(3) 部分命题2
2.余维数:



3.标准映射
(1)概念:


(2)标准映射与补空间:
这也就是 线性空间.线性空间与子空间.二.3.(3) 部分命题3’的证明
命题2:域 F F F上线性空间 V V V的任一子空间 W W W都有补空间 U U U
该命题表明,如果知道了商空间 V / W V/W V/W的1个基,那么 V = W ⊕ U V=W\oplus U V=W⊕U,这样 V V V就有了1个直和式分解;这是可以利用商空间研究线性空间的结构的道理之三
附录.集合的划分,等价关系,等价类
1.集合的划分:

2.等价关系与等价类
(1)二元关系:
二元关系:设 S S S是1个非空集合, S × S S×S S×S( S S S和 S S S的笛卡儿积)的1个子集 W W W称为 S S S上的1个二元关系
若 ( a , b ) ∈ W (a,b)∈W (a,b)∈W,则称 a a a与 b b b具有 W W W关系,记作 a ∼ W b a\sim_Wb a∼Wb或 a ∼ b a\sim b a∼b
若 ( a , b ) ∉ W (a,b)\notin W (a,b)∈/W,则称 a a a与 b b b没有 W W W关系
(2)等价关系
等价关系:满足反身性(或称自反性),对称性,传递性的二元关系称为等价关系
(3)等价类:
等价类:设R是定义在集合S中的等价关系,a为S中的某个元素,则S中和a具有关系R的所有元素的集合称为关于R的等价类,记作 [ a ] R , a [a]_R,a [a]R,a称为该等价类的1个代表;当只考虑1个关系时,可以省去下标R,简记作[a]
注意:①也可以称为S的1个等价类
②1个等价类的代表不唯一,其中的任何1个元素都可以作为代表;
③当选定某等价类的代表为 a 0 a_0 a0时,可以称该等价类为a0的(关于R的)等价类,记作 a 0 ˉ : = { x ∈ S ∣ x ∼ a 0 } \bar{a_0}:=\{x∈S\,|\,x\sim a_0\} a0ˉ:={x∈S∣x∼a0}
(4)等价类的性质:
性质1: a ˉ = b ˉ \bar a=\bar b aˉ=bˉ的充要条件是: a ∼ b a\sim b a∼b
性质2:若 a ˉ ≠ b ˉ \bar a≠\bar b aˉ=bˉ,则 a ˉ ∩ b ˉ = Φ \bar a∩\bar b=Φ aˉ∩bˉ=Φ
(5)所有等价类构成集合的1个划分:
定理2:如果集合 S S S上有1个等价关系 R R R,那么所有关于 R R R的等价类组成的集合就是 S S S的1个划分
反之,如果集合 S S S有1个划分,那么一定可以在 S S S上建立1个等价关系R,使得这个划分是由关于 R R R的所有等价类组成的








 本文深入探讨了线性空间同构的基本概念、性质及判定方法,包括同构映射的特性、子空间同构、同构类与有限域元素个数的关系。同时,介绍了商空间的概念、维数计算及其与补空间的关系,强调了通过商空间研究线性空间结构的重要性。
本文深入探讨了线性空间同构的基本概念、性质及判定方法,包括同构映射的特性、子空间同构、同构类与有限域元素个数的关系。同时,介绍了商空间的概念、维数计算及其与补空间的关系,强调了通过商空间研究线性空间结构的重要性。



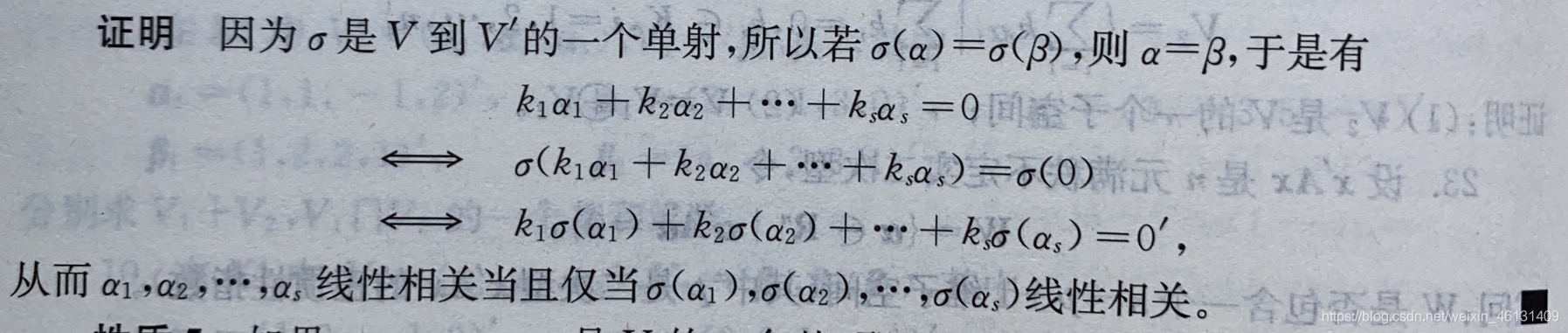











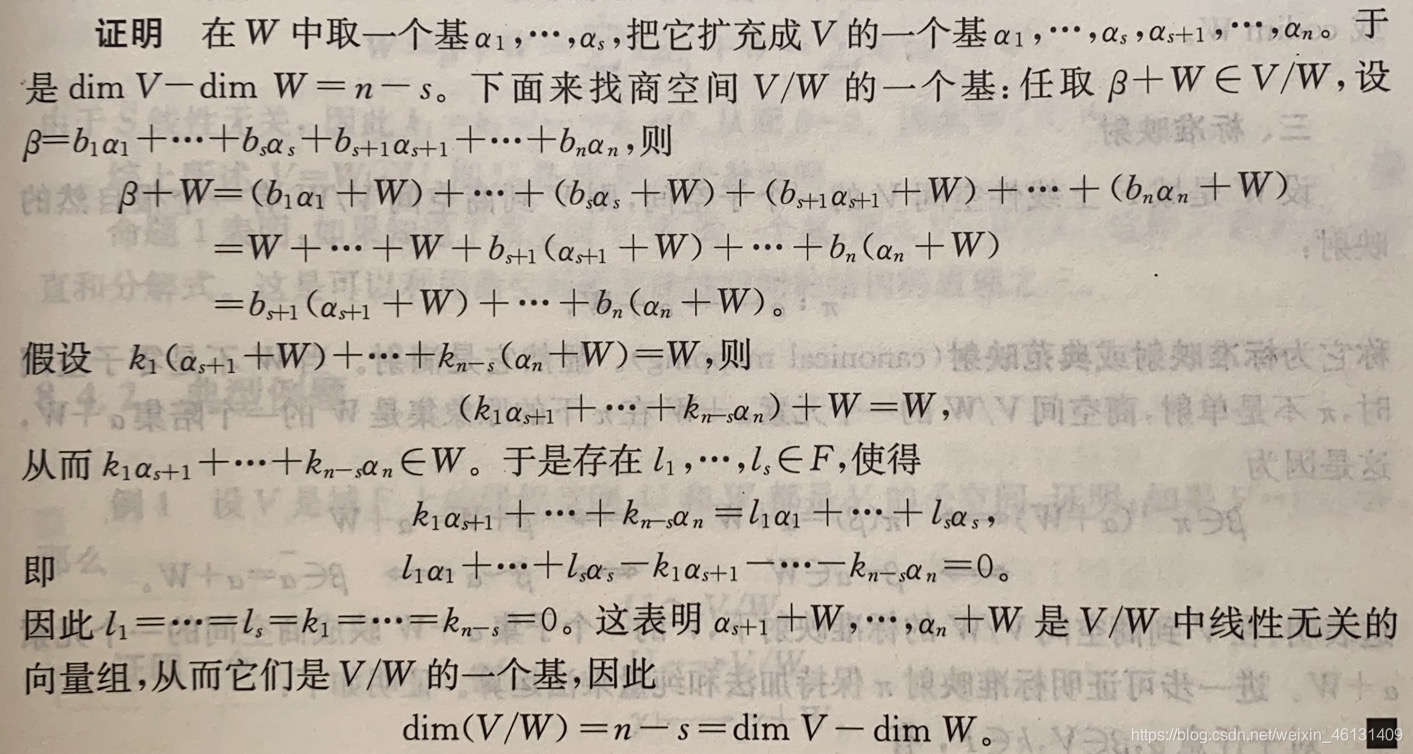





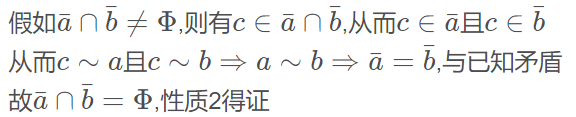


















 3842
3842

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








