文章目录
李群: 表征旋转矩阵R或变换矩阵RT的集合
李代数: 描述旋转矩阵R或变换矩阵RT的导数关系
作用是解决矩阵求导问题, 解决微小扰动等问题
4.1.基础
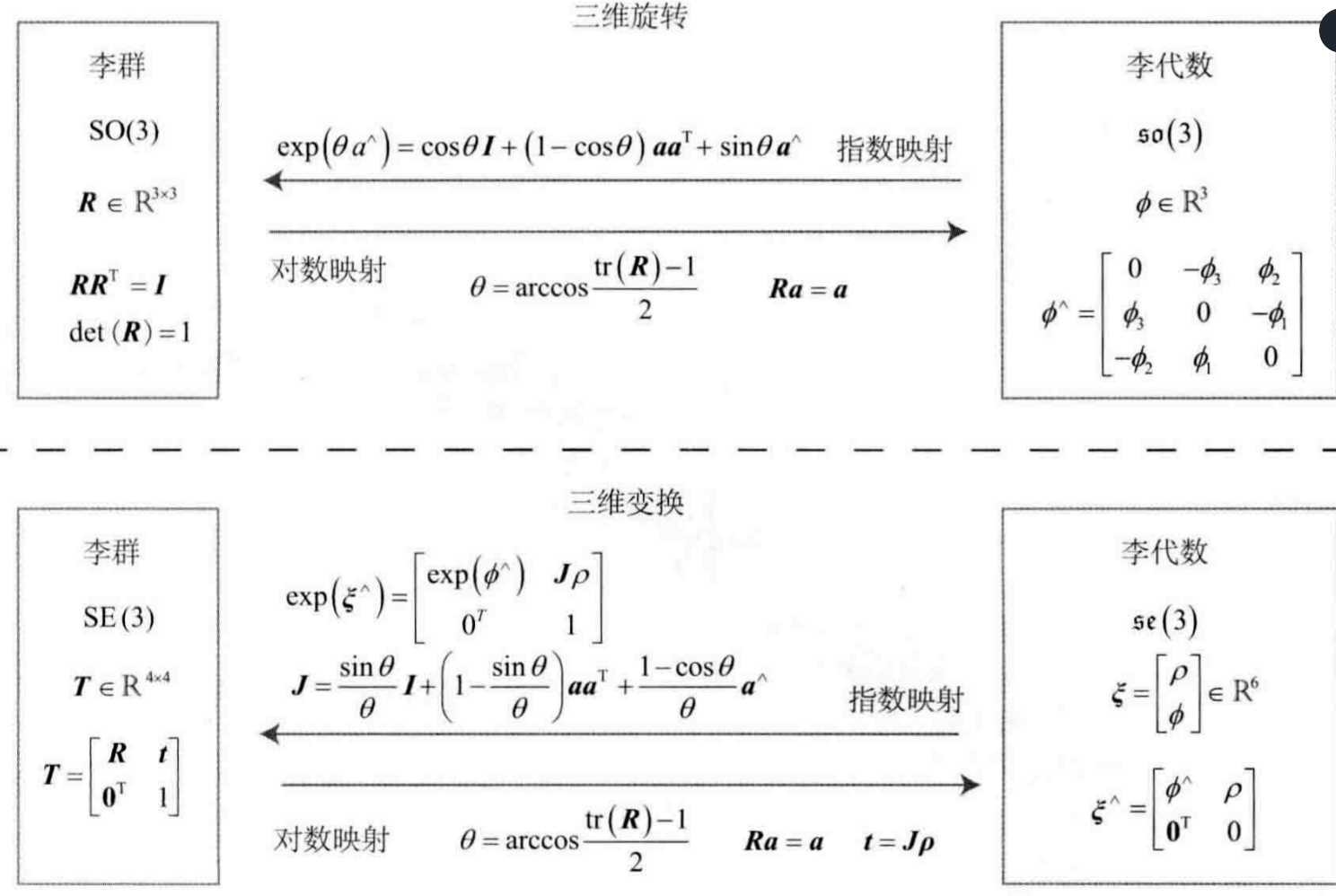
- 旋转矩阵++=特殊正交群 S O ( 3 ) SO(3) SO(3) SO ( 3 ) = { R ∈ R 3 × 3 ∣ R R T = I , det ( R ) = 1 } \operatorname{SO}(3)=\left\{\boldsymbol{R} \in \mathbb{R}^{3 \times 3} \mid \boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\} SO(3)={R∈R3×3∣RRT=I,det(R)=1}
- 变换矩阵++=特殊欧式群 S E ( 3 ) SE(3) SE(3) S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } \mathrm{SE}(3)=\left\{\boldsymbol{T}=\left[\begin{array}{cc}\boldsymbol{R} & \boldsymbol{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in \mathrm{SO}(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\} SE(3)={T=[R0Tt1]∈R4×4∣R∈SO(3),t∈R3}
- 对加法不封闭,对乘法封闭 R 1 + R 2 ∉ S O ( 3 ) , T 1 + T 2 ∉ S E ( 3 ) \boldsymbol{R}_{1}+\boldsymbol{R}_{2} \notin \mathrm{SO}(3), \quad \boldsymbol{T}_{1}+\boldsymbol{T}_{2} \notin \mathrm{SE}(3) R1+R2∈/SO(3),T1+T2∈/SE(3) ~~~~ R 1 R 2 ∈ S O ( 3 ) , T 1 T 2 ∈ S E ( 3 ) \boldsymbol{R}_{1} \boldsymbol{R}_{2} \in \mathrm{SO}(3), \quad \boldsymbol{T}_{1} \boldsymbol{T}_{2} \in \mathrm{SE}(3) R1R2∈SO(3),T1T2∈SE(3)
群
- 群: 一种集合+一种运算的代数结构 集合A 运算· 群G=(A,·)
- 封闭性 ∀ a 1 , a 2 ∈ A , a 1 ⋅ a 2 ∈ A \forall a_{1}, a_{2} \in A, \quad a_{1} \cdot a_{2} \in A ∀a1,a2∈A,a1⋅a2∈A
- 结合律 ∀ a 1 , a 2 , a 3 ∈ A , ( a 1 ⋅ a 2 ) ⋅ a 3 = a 1 ⋅ ( a 2 ⋅ a 3 ) \forall a_{1}, a_{2}, a_{3} \in A, \quad\left(a_{1} \cdot a_{2}\right) \cdot a_{3}=a_{1} \cdot\left(a_{2} \cdot a_{3}\right) ∀a1,a2,a3∈A,(a1⋅a2)⋅a3=a1⋅(a2⋅a3)
- 幺元 ∃ a 0 ∈ A , s.t. ∀ a ∈ A , a 0 ⋅ a = a ⋅ a 0 = a \exists a_{0} \in A, \quad \text { s.t. } \quad \forall a \in A, \quad a_{0} \cdot a=a \cdot a_{0}=a ∃a0∈A, s.t. ∀a∈A,a0⋅a=a⋅a0=a
- 逆 ∀ a ∈ A , ∃ a − 1 ∈ A , s.t. a ⋅ a − 1 = a 0 \forall a \in A, \quad \exists a^{-1} \in A, \quad \text { s.t. } \quad a \cdot a^{-1}=a_{0} ∀a∈A,∃a−1∈A, s.t. a⋅a−1=a0
- 常见
- 整数加法 ( Z , + ) (Z,+) (Z,+) ~~~~ 不含0有理数乘法 ( Q ∖ 0 , ⋅ ) (Q\setminus 0,·) (Q∖0,⋅)
- 一般线性群GL(n) nxn可逆矩阵, 对矩阵乘法成群
- 特殊正交群SO(n) 旋转矩阵群 SO(2) SO(3)
- 特殊欧氏群SE(n) 欧氏变换 SE(2) SE(3)
- 李群: 连续(光滑)性质的群 SO(n) SE(n) 能连续运动
李代数的引出
-
李代数
- 任意旋转矩阵R满足 R R T = I RR^T=I RRT=I
- 反对称换算 a ∧ = A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] , A ∨ = a \boldsymbol{a}^{\wedge}=\boldsymbol{A}=\left[\begin{array}{ccc}0 & -a_{3} & a_{2} \\a_{3} & 0 & -a_{1} \\-a_{2} & a_{1} & 0\end{array}\right], \quad \boldsymbol{A}^{\vee}=\boldsymbol{a} a∧=A=⎣ ⎡0a3−a2−a30a1a2−a10⎦ ⎤,A∨=a
- 等式两边求导得反对称矩阵 R ˙ ( t ) R ( t ) T = − ( R ˙ ( t ) R ( t ) T ) T = ϕ ( t ) ∧ \dot{\boldsymbol{R}}(t) \boldsymbol{R}(t)^{\mathrm{T}}=-\left(\dot{\boldsymbol{R}}(t) \boldsymbol{R}(t)^{\mathrm{T}}\right)^{\mathrm{T}} = \phi(t)^{\wedge} R˙(t)R(t)T=−(R˙(t)R(t)T)T=ϕ(t)∧
- 每对旋转矩阵求一次导, 左乘一个
ϕ
∧
(
t
)
\phi^\wedge(t)
ϕ∧(t)矩阵,
R
˙
(
t
)
=
ϕ
0
∧
R
(
t
)
\dot{R}(t)=\phi_0^{\wedge}R(t)
R˙(t)=ϕ0∧R(t)
- 解得 R ( t ) = exp ( ϕ 0 ∧ t ) \textbf{R}(t)=\exp(\phi_0^{\wedge}t) R(t)=exp(ϕ0∧t) 说明 t = 0 t=0 t=0附近, 旋转矩阵可由 exp ( ϕ 0 ˆ t ) \exp(\phi_0\^{}t) exp(ϕ0ˆt)计算
- 给定某时刻 R R R, 求得一个 ϕ \phi ϕ, 描述了 R R R在局部的导数关系: ϕ \phi ϕ正是对应到 S O ( 3 ) SO(3) SO(3)上的李代数 s o ( 3 ) \mathfrak{so}(3) so(3)
- 给定向量 ϕ \phi ϕ计算矩阵指数 exp ( ϕ ∧ ) \exp(\phi^\wedge) exp(ϕ∧); 给定 R R R计算 ϕ \phi ϕ: 指数/对数映射
李代数
- 一个集合V, 一个数域F, 一个二元运算[,]组成, 满足以下性质则(V,F,[,])为一个李代数
- 性质
- 封闭性 ∀ X , Y ∈ V , [ X , Y ] ∈ V \forall \boldsymbol{X}, \boldsymbol{Y} \in \mathbb{V},[\boldsymbol{X}, \boldsymbol{Y}] \in \mathbb{V} ∀X,Y∈V,[X,Y]∈V
- 双线性 ∀ X , Y , Z ∈ V , a , b ∈ F \forall \boldsymbol{X}, \boldsymbol{Y}, \boldsymbol{Z} \in \mathbb{V}, a, b \in \mathbb{F} ∀X,Y,Z∈V,a,b∈F 有 { [ a X + b Y , Z ] = a [ X , Z ] + b [ Y , Z ] [ Z , a X + b Y ] = a [ Z , X ] + b [ Z , Y ] \left\{\begin{matrix}[a \boldsymbol{X}+b \boldsymbol{Y}, \boldsymbol{Z}]=a[\boldsymbol{X}, \boldsymbol{Z}]+b[\boldsymbol{Y}, \boldsymbol{Z}] \\ [\boldsymbol{Z}, a \boldsymbol{X}+b \boldsymbol{Y}]=a[\boldsymbol{Z}, \boldsymbol{X}]+b[\boldsymbol{Z}, \boldsymbol{Y}]\end{matrix}\right. {[aX+bY,Z]=a[X,Z]+b[Y,Z][Z,aX+bY]=a[Z,X]+b[Z,Y]
- 自反性 ∀ X ∈ V , [ X , X ] = 0 \forall \boldsymbol{X} \in \mathbb{V},[\boldsymbol{X}, \boldsymbol{X}]=\mathbf{0} ∀X∈V,[X,X]=0
- 雅可比等价 ∀ X , Y , Z ∈ V , [ X , [ Y , Z ] ] + [ Z , [ X , Y ] ] + [ Y , [ Z , X ] ] = 0 \forall \boldsymbol{X}, \boldsymbol{Y}, \boldsymbol{Z} \in \mathbb{V},[\boldsymbol{X},[\boldsymbol{Y}, \boldsymbol{Z}]]+[\boldsymbol{Z},[\boldsymbol{X}, \boldsymbol{Y}]]+[\boldsymbol{Y},[\boldsymbol{Z}, \boldsymbol{X}]]=\mathbf{0} ∀X,Y,Z∈V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0
- 李括号[,]
- 表达了两个元素的差异
- 三维向量 R 3 R^3 R3定义的叉积是一种李括号, g = ( R 3 , R , x ) g=(R^3,R,\rm x) g=(R3,R,x)构成一个李代数
李代数 s o ( 3 ) \mathfrak{so}(3) so(3)
- SO(3)对应的李代数是定义于
R
3
R^3
R3上的向量, 记作
ϕ
\phi
ϕ, 每个
ϕ
\phi
ϕ可生成一个反对称阵
Φ
=
ϕ
∧
\varPhi = \phi^{\wedge}
Φ=ϕ∧
- 李括号 [ ϕ 1 , ϕ 2 ] = ( Φ 1 Φ 2 − Φ 2 Φ 1 ) ∨ [\phi_1,\phi_2] = (\Phi_1\Phi_2- \Phi_2\Phi_1)^{\vee} [ϕ1,ϕ2]=(Φ1Φ2−Φ2Φ1)∨
-
s
o
(
3
)
=
{
ϕ
∈
R
3
,
Φ
=
ϕ
∧
∈
R
3
×
3
}
\mathfrak{so}(3)=\{\phi\in R^3,\Phi=\phi^{\wedge}\in R^{3\times3}\}
so(3)={ϕ∈R3,Φ=ϕ∧∈R3×3}
- 由三维向量组成的集合, 每个向量对应一个反对称阵, 以表达旋转矩阵的导数
- 与 S O ( 3 ) SO(3) SO(3)的关系 R = exp ( ϕ ∧ ) R=\exp(\phi^{\wedge}) R=exp(ϕ∧)
李代数 s e ( 3 ) \mathfrak{se}(3) se(3)
- 李代数
s
e
(
3
)
=
{
ξ
=
[
ρ
ϕ
]
∈
R
6
,
ρ
∈
R
3
,
ϕ
∈
s
o
(
3
)
,
ξ
∧
=
[
ϕ
∧
ρ
0
T
0
]
∈
R
4
×
4
}
\mathfrak{s e}(3)=\left\{\boldsymbol{\xi}=\left[\begin{array}{l}\boldsymbol{\rho} \\\phi\end{array}\right] \in \mathbb{R}^{6}, \boldsymbol{\rho} \in \mathbb{R}^{3}, \phi \in \mathfrak{s o}(3), \boldsymbol{\xi}^{\wedge}=\left[\begin{array}{cc}\phi^{\wedge} & \rho \\\mathbf{0}^{\mathrm{T}} & 0\end{array}\right] \in \mathbb{R}^{4 \times 4}\right\}
se(3)={ξ=[ρϕ]∈R6,ρ∈R3,ϕ∈so(3),ξ∧=[ϕ∧0Tρ0]∈R4×4}
- 六维向量 ξ \xi ξ, 平移 ρ \rho ρ, 旋转 ϕ \phi ϕ, 向量->矩阵 ∧ ^\wedge ∧, 矩阵->向量 ∨ ^\vee ∨
- 括号 [ ξ 1 , ξ 2 ] = ( ξ 1 ∧ ξ 2 ∧ − ξ 2 ∧ ξ 1 ∧ ) ∨ [\xi_1,\xi_2]=(\xi_1^\wedge\xi_2^\wedge-\xi_2^\wedge\xi_1^\wedge)^\vee [ξ1,ξ2]=(ξ1∧ξ2∧−ξ2∧ξ1∧)∨
4.2.指数与对数映射
4.2.1. S O ( 3 ) SO(3) SO(3)指数映射
- 对
s
o
(
3
)
\mathfrak{so}(3)
so(3)的任意元素
ϕ
\phi
ϕ, 定义指数映射 $\exp(\phi\wedge)=\sum_{n=0}{\infty}\frac{1}{n!}(\phi\wedge)n $
- 一顿推导得 exp ( θ a ∧ ) = cos θ I + ( 1 − cos θ ) a a T + sin θ a ∧ \exp(\theta a^\wedge)=\cos\theta I +(1-\cos\theta)aa^T+\sin\theta a^\wedge exp(θa∧)=cosθI+(1−cosθ)aaT+sinθa∧ (罗德里格斯公式-从旋转向量到旋转矩阵的转换)
- 表明 s o ( 3 ) \mathfrak{so}(3) so(3)是旋转向量组成的空间
- 对数映射 ϕ = ln ( R ) ∨ = ( ∑ n = 0 ∞ ( − 1 ) n n + 1 ( R − I ) n + 1 ) ∨ \phi=\ln(R)^\vee=(\sum_{n=0}^\infty\frac{(-1)^n}{n+1}(R-I)^{n+1})^\vee ϕ=ln(R)∨=(∑n=0∞n+1(−1)n(R−I)n+1)∨
- 指数映射是满射
- 每个 S O ( 3 ) SO(3) SO(3)的元素可以找到一个 s o ( 3 ) \mathfrak{so}(3) so(3)元素对应
- 可能存在多个
s
o
(
3
)
\mathfrak{so}(3)
so(3)元素对应同一个
S
O
(
3
)
SO(3)
SO(3)
- 对旋转角 θ \theta θ, 多转 36 0 ∘ 360^\circ 360∘和没转一样
- 指数映射即罗德里格斯公式
- 旋转矩阵的导数可由旋转向量指定, 指导如何在旋转矩阵中进行微积分运算
4.2.2. S E ( 3 ) SE(3) SE(3)的指数映射
-
exp
(
ξ
∧
)
=
[
∑
n
=
0
∞
1
n
!
(
ϕ
∧
)
n
∑
n
=
0
∞
1
(
n
+
1
)
!
(
ϕ
∧
)
n
ρ
0
T
]
≜
[
R
J
ρ
0
T
1
]
=
T
.
\begin{aligned}\exp \left(\boldsymbol{\xi}^{\wedge}\right) &=\left[\begin{array}{cc}\sum_{n=0}^{\infty} \frac{1}{n !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} & \sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}}\end{array}\right] \\& \triangleq\left[\begin{array}{cc}\boldsymbol{R} & \boldsymbol{J} \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right]=\boldsymbol{T} .\end{aligned}
exp(ξ∧)=[∑n=0∞n!1(ϕ∧)n0T∑n=0∞(n+1)!1(ϕ∧)nρ]≜[R0TJρ1]=T.
- 左上角的R是 S O ( 3 ) SO(3) SO(3)的元素, 与 s e ( 3 ) \mathfrak{se}(3) se(3)的旋转部分 ϕ \phi ϕ对应
- 右上角
J
=
sin
θ
θ
I
+
(
1
−
sin
θ
θ
)
a
a
T
+
1
−
cos
θ
θ
a
∧
\boldsymbol{J}=\frac{\sin \theta}{\theta} \boldsymbol{I}+\left(1-\frac{\sin \theta}{\theta}\right) \boldsymbol{a} \boldsymbol{a}^{\mathrm{T}}+\frac{1-\cos \theta}{\theta} \boldsymbol{a}^{\wedge}
J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧
- 平移部分经指数映射后, 发生了一次以 J J J为系数矩阵的线性变换
- 左上角的 R R R计算旋转向量, 右上角的 t t t满足 t = J ρ t=J\rho t=Jρ
4.3.李代数求导与扰动模型
4.3.1.BCH公式&近似形式
-
ln
(
exp
(
A
)
exp
(
B
)
)
=
A
+
B
+
1
2
[
A
,
B
]
+
1
12
[
A
,
[
A
,
B
]
]
−
1
12
[
B
,
[
A
,
B
]
]
+
⋯
\ln (\exp (\boldsymbol{A}) \exp (\boldsymbol{B}))=\boldsymbol{A}+\boldsymbol{B}+\frac{1}{2}[\boldsymbol{A}, \boldsymbol{B}]+\frac{1}{12}[\boldsymbol{A},[\boldsymbol{A}, \boldsymbol{B}]]-\frac{1}{12}[\boldsymbol{B},[\boldsymbol{A}, \boldsymbol{B}]]+\cdots
ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+⋯
- 两个矩阵指数积, 会产生一些由李括号组成的余项
-
S
O
(
3
)
SO(3)
SO(3)
- 旋转
R
R
R-李代数
ϕ
\phi
ϕ, 左乘一个微小旋转
Δ
R
\Delta R
ΔR-李代数
Δ
ϕ
\Delta\phi
Δϕ, 则李群上得
Δ
R
⋅
R
\Delta R\cdot R
ΔR⋅R, 李代数
J
l
−
1
(
ϕ
)
Δ
ϕ
+
ϕ
J_l^{-1}(\phi)\Delta\phi+\phi
Jl−1(ϕ)Δϕ+ϕ
- exp ( Δ ϕ ∧ ) exp ( ϕ ∧ ) = exp ( ( ϕ + J l − 1 ( ϕ ) Δ ϕ ) ∧ ) \exp \left(\Delta \phi^{\wedge}\right) \exp \left(\phi^{\wedge}\right)=\exp \left(\left(\phi+J_{l}^{-1}(\phi) \Delta \phi\right)^{\wedge}\right) exp(Δϕ∧)exp(ϕ∧)=exp((ϕ+Jl−1(ϕ)Δϕ)∧)
- 李代数加法,
ϕ
+
Δ
ϕ
\phi + \Delta\phi
ϕ+Δϕ, 近似为李群上带左右雅可比的乘法
- exp ( ( ϕ + Δ ϕ ) ∧ ) = exp ( ϕ ∧ ) exp ( ( J r Δ ϕ ) ∧ ) \exp((\phi+\Delta\phi)^\wedge)=\exp(\phi^\wedge)\exp((J_r\Delta\phi)^\wedge) exp((ϕ+Δϕ)∧)=exp(ϕ∧)exp((JrΔϕ)∧)
- 此为之后做微积分的理论基础
- 旋转
R
R
R-李代数
ϕ
\phi
ϕ, 左乘一个微小旋转
Δ
R
\Delta R
ΔR-李代数
Δ
ϕ
\Delta\phi
Δϕ, 则李群上得
Δ
R
⋅
R
\Delta R\cdot R
ΔR⋅R, 李代数
J
l
−
1
(
ϕ
)
Δ
ϕ
+
ϕ
J_l^{-1}(\phi)\Delta\phi+\phi
Jl−1(ϕ)Δϕ+ϕ
-
S
E
(
3
)
SE(3)
SE(3)
- exp ( Δ ξ ∧ ) exp ( ξ ∧ ) ≈ exp ( ( J l − 1 Δ ξ + ξ ) ∧ ) exp ( ξ ∧ ) exp ( Δ ξ ∧ ) ≈ exp ( ( J r − 1 Δ ξ + ξ ) ∧ ) \begin{array}{l}\exp \left(\Delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \approx \exp \left(\left(\mathcal{J}_{l}^{-1} \Delta \boldsymbol{\xi}+\boldsymbol{\xi}\right)^{\wedge}\right) \\\exp \left(\boldsymbol{\xi}^{\wedge}\right) \exp \left(\Delta \boldsymbol{\xi}^{\wedge}\right) \approx \exp \left(\left(\mathcal{J}_{r}^{-1} \Delta \boldsymbol{\xi}+\boldsymbol{\xi}\right)^{\wedge}\right)\end{array} exp(Δξ∧)exp(ξ∧)≈exp((Jl−1Δξ+ξ)∧)exp(ξ∧)exp(Δξ∧)≈exp((Jr−1Δξ+ξ)∧)
4.3.2.李代数求导
- 小萝卜位姿T, 观察到世界坐标位于p的点
z
=
T
p
+
w
z=Tp+w
z=Tp+w
- 观测与实际数据误差 e = z − T p e=z-Tp e=z−Tp
- 寻找一个最优T使整体误差最小化 min T J ( T ) = ∑ i = 1 N ∣ ∣ z i − T p i ∣ ∣ 2 2 \min_T J(T)=\sum_{i=1}^N||z_i-Tp_i||_2^2 minTJ(T)=∑i=1N∣∣zi−Tpi∣∣22
- 构建与位姿有关函数, 讨论该函数关于位姿的导数, 调整当前估计值
- 李代数表示姿态, 据李代数加法对李代数求导
- 对李群左乘/右乘微小扰动, 对扰动求导称左扰动/右扰动模型
4.3.4.扰动模型(左乘)
- 对
R
R
R进行一次扰动
Δ
R
\Delta R
ΔR(李代数
φ
\varphi
φ), 对
φ
\varphi
φ求导
- ∂ ( R p ) ∂ φ = lim φ → 0 exp ( φ ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p φ = lim φ → 0 ( I + φ ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p φ = lim φ → 0 φ ∧ R p φ = lim φ → 0 − ( R p ) ∧ φ φ = − ( R p ) ∧ \begin{aligned}\frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}} &=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\exp \left(\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\boldsymbol{\varphi}} \\&=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\left(\boldsymbol{I}+\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\boldsymbol{\varphi}} \\&=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\boldsymbol{\varphi}^{\wedge} \boldsymbol{R} \boldsymbol{p}}{\boldsymbol{\varphi}}=\lim _{\boldsymbol{\varphi} \rightarrow \mathbf{0}} \frac{-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{\varphi}}{\boldsymbol{\varphi}}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge}\end{aligned} ∂φ∂(Rp)=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφ(I+φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφφ∧Rp=φ→0limφ−(Rp)∧φ=−(Rp)∧
4.3.5. S E ( 3 ) SE(3) SE(3)李代数求导
-
∂
(
T
p
)
∂
δ
ξ
=
lim
δ
ξ
→
0
exp
(
δ
ξ
∧
)
exp
(
ξ
∧
)
p
−
exp
(
ξ
∧
)
p
δ
ξ
=
lim
δ
ξ
→
0
(
I
+
δ
ξ
∧
)
exp
(
ξ
∧
)
p
−
exp
(
ξ
∧
)
p
δ
ξ
=
lim
δ
ξ
→
0
δ
ξ
∧
exp
(
ξ
∧
)
p
δ
ξ
=
lim
δ
ξ
→
0
[
δ
ϕ
∧
δ
ρ
0
T
0
]
[
R
p
+
t
1
]
δ
ξ
=
lim
δ
ξ
→
0
[
δ
ϕ
∧
(
R
p
+
t
)
+
δ
ρ
0
T
]
[
δ
ρ
,
δ
ϕ
]
T
=
[
I
−
(
R
p
+
t
)
∧
0
T
0
T
]
=
def
(
T
p
)
⊙
.
\frac{\partial(\boldsymbol{T} \boldsymbol{p})}{\partial \delta \boldsymbol{\xi}}\\\begin{array}{l}=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\exp \left(\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\xi}}\\=\lim _{\delta \boldsymbol{\xi} \rightarrow \mathbf{0}} \frac{\left(\boldsymbol{I}+\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\xi}} \\=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\delta \boldsymbol{\xi}^{\wedge} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\xi}} \\=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left[\begin{array}{cc}\delta \boldsymbol{\phi}^{\wedge} & \delta \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}} & 0\end{array}\right]\left[\begin{array}{c}\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t} \\1\end{array}\right]}{\delta \boldsymbol{\xi}} \\=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left[\begin{array}{c}\delta \boldsymbol{\phi}^{\wedge}(\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t})+\delta \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}}\end{array}\right]}{[\delta \boldsymbol{\rho}, \delta \boldsymbol{\phi}]^{\mathrm{T}}}=\left[\begin{array}{cc}\boldsymbol{I} & -(\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t})^{\wedge} \\\mathbf{0}^{\mathrm{T}} & \mathbf{0}^{\mathrm{T}}\end{array}\right] \stackrel{\text { def }}{=}(\boldsymbol{T} \boldsymbol{p})^{\odot} .\end{array}
∂δξ∂(Tp)=limδξ→0δξexp(δξ∧)exp(ξ∧)p−exp(ξ∧)p=limδξ→0δξ(I+δξ∧)exp(ξ∧)p−exp(ξ∧)p=limδξ→0δξδξ∧exp(ξ∧)p=limδξ→0δξ[δϕ∧0Tδρ0][Rp+t1]=limδξ→0[δρ,δϕ]T[δϕ∧(Rp+t)+δρ0T]=[I0T−(Rp+t)∧0T]= def (Tp)⊙.
- 矩阵求导 d [ a b ] d [ x y ] = ( d [ a , b ] T d [ x y ] ) T = [ d a d x d b d x d a d y d b d y ] T = [ d a d x d a d y d b d x d b d y ] \frac{\mathrm{d}\left[\begin{array}{l}\boldsymbol{a} \\\boldsymbol{b}\end{array}\right]}{\mathrm{d}\left[\begin{array}{l}\boldsymbol{x} \\\boldsymbol{y}\end{array}\right]}=\left(\frac{\mathrm{d}[\boldsymbol{a}, \boldsymbol{b}]^{\mathrm{T}}}{\mathrm{d}\left[\begin{array}{l}\boldsymbol{x} \\\boldsymbol{y}\end{array}\right]}\right)^{\mathrm{T}}=\left[\begin{array}{ll}\frac{\mathrm{d} \boldsymbol{a}}{\mathrm{d} \boldsymbol{x}} & \frac{\mathrm{d} \boldsymbol{b}}{\mathrm{d} \boldsymbol{x}} \\\frac{\mathrm{d} \boldsymbol{a}}{\mathrm{d} \boldsymbol{y}} & \frac{\mathrm{d} \boldsymbol{b}}{\mathrm{d} \boldsymbol{y}}\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{cc}\frac{\mathrm{d} \boldsymbol{a}}{\mathrm{d} \boldsymbol{x}} & \frac{\mathrm{d} \boldsymbol{a}}{\mathrm{d} \boldsymbol{y}} \\\frac{\mathrm{d} \boldsymbol{b}}{\mathrm{d} \boldsymbol{x}} & \frac{\mathrm{d} \boldsymbol{b}}{\mathrm{d} \boldsymbol{y}}\end{array}\right] d[xy]d[ab]=⎝ ⎛d[xy]d[a,b]T⎠ ⎞T=[dxdadydadxdbdydb]T=[dxdadxdbdydadydb]
4.5.相似变换
- 单目视觉下存在尺度不确定性
- 若用 S E ( 3 ) SE(3) SE(3)表示位姿, 由于尺度不确定性与尺度漂移, 整个SLAM过程的尺度会发生变化
- 显式地表达尺度因子, 对空间点p, 相机坐标系下经过一个相似变换, 而非欧氏变换
-
p
′
=
[
s
R
t
0
T
1
]
p
=
s
R
p
+
t
\boldsymbol{p}^{\prime}=\left[\begin{array}{ll}s \boldsymbol{R} & \boldsymbol{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \boldsymbol{p}=s \boldsymbol{R} \boldsymbol{p}+\boldsymbol{t}
p′=[sR0Tt1]p=sRp+t
- 尺度s同时作用在p的三个坐标上, 对其进行缩放
- 相似变换群 Sim ( 3 ) = { S = [ s R t 0 T 1 ] ∈ R 4 × 4 } \operatorname{Sim}(3)=\left\{\boldsymbol{S}=\left[\begin{array}{ll}s \boldsymbol{R} & \boldsymbol{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \in \mathbb{R}^{4 \times 4}\right\} Sim(3)={S=[sR0Tt1]∈R4×4}
- 李代数
-
p
′
=
[
s
R
t
0
T
1
]
p
=
s
R
p
+
t
\boldsymbol{p}^{\prime}=\left[\begin{array}{ll}s \boldsymbol{R} & \boldsymbol{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \boldsymbol{p}=s \boldsymbol{R} \boldsymbol{p}+\boldsymbol{t}
p′=[sR0Tt1]p=sRp+t
实现
main.cpp
#include <iostream>
#include <cmath>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Geometry>
#include "sophus/se3.hpp"
#include <pangolin/pangolin.h>
#include <unistd.h>
using namespace std;
using namespace Eigen;
typedef vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> TrajectoryType;
typedef vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> PosesType;
void Change_SO3();
void Change_SE3();
void DrawTrajectory(vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses);
void test_play(string TrajectFile);
void test_play2(string TrajectFile1, string TrajectFile2);
TrajectoryType ReadTrajectory(const string &path);
string estimated_file = "../estimated.txt"; // 在build文件的上一级寻找
string groundtruth_file = "../groundtruth.txt"; // 在build文件的上一级寻找
int main(int argc, char **argv)
{
// Change_SO3();
// Change_SE3();
// test_play(estimated_file);
test_play2(groundtruth_file,estimated_file);
TrajectoryType ExtimateData = ReadTrajectory(estimated_file);
TrajectoryType GroundData = ReadTrajectory(groundtruth_file);
assert(!ExtimateData.empty() && !GroundData.empty());
assert(ExtimateData.size() == GroundData.size());
double rmse = 0;
for(size_t i=0;i<ExtimateData.size();i++)
{
Sophus::SE3d p1 = ExtimateData[i], p2 = GroundData[i];
double error = (p2.inverse() * p1).log().norm();
rmse += error * error;
}
rmse = rmse / double(ExtimateData.size());
rmse = sqrt(rmse);
cout << "\nRMSE = " << rmse << endl;
return 0;
}
void Change_SO3()
{
// 沿y轴旋转90度的矩阵
Matrix3d R = AngleAxisd(M_PI_2, Vector3d(0,1,0)).toRotationMatrix();
Sophus::SO3d SO3_R(R);
cout << "\nSO(3) from matrix:\n" << SO3_R.matrix() << endl;
// 四元数创建也一样
Quaterniond q(R);
Sophus::SO3d SO3_q(q);
cout << "\nSO(3) from quaternion:\n" << SO3_q.matrix() << endl;
// 对数映射得李代数
Vector3d so3 = SO3_R.log();
cout << "\nso3:\n" << so3.transpose() << endl;
// hat向量->反对称阵
Matrix3d so3hat = Sophus::SO3d::hat(so3);
cout << "\nso3hat:\n" << so3hat << endl;
// vee反对称阵->向量
Vector3d so3vee = Sophus::SO3d::vee(so3hat).transpose();
cout << "\nso3vee:\n" << so3vee << endl;
// 增量扰动模型更新
Vector3d update_so3(1e-4,0,0);
Sophus::SO3d SO3_updated = Sophus::SO3d::exp(update_so3) * SO3_R;
cout << "\nSO(3) updated:\n" << SO3_updated.matrix() << endl;
}
void Change_SE3()
{
// 沿y轴旋转90度的矩阵
Matrix3d R = AngleAxisd(M_PI_2, Vector3d(0,1,0)).toRotationMatrix();
Quaterniond q(R);
Vector3d t(1,0,0); // 沿x轴平移1
Sophus::SE3d SE3_Rt(R,t); // 从Rt构造SE(3)
cout << "\nSE3 from R,t:\n" << SE3_Rt.matrix() << endl;
Sophus::SE3d SE3_qt(q,t); // 从qt构造SE(3)
cout << "\nSE3 from q,t:\n" << SE3_qt.matrix() << endl;
typedef Eigen::Matrix<double,6,1> Vector6d; // 李代数是一个六维向量
typedef Eigen::Matrix<double,4,4> Matrix6d; // 李代数是一个六维向量
Vector6d se3 = SE3_Rt.log(); // 取李代数
cout << "\nse3:\n" << se3.transpose() << endl;
Matrix6d se3hat = Sophus::SE3d::hat(se3);
cout << "\nse3 hat\n" << se3hat << endl;
Vector6d se3vee = Sophus::SE3d::vee(se3hat).transpose();
cout << "\nse3 vee\n" << se3vee << endl;
// 增量扰动模型更新
Vector6d update_se3;
update_se3.setZero();
update_se3(0,0) = 1e-4d;
Sophus::SE3d SE3_updated = Sophus::SE3d::exp(update_se3) * SE3_Rt;
cout << "\nSE3 update\n" << SE3_updated.matrix() << endl;
}
void DrawTrajectory(PosesType poses)
{
pangolin::CreateWindowAndBind("Viewer",1024,768);
glEnable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024,768,500,500,512,389,0.1,1000),
pangolin::ModelViewLookAt(0,-0.1,-1.8,0,0,0,0.0,-1.0,0.0)
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0,1.0,0.0,1.0,-1024.0f/768.0f)
.SetHandler(new pangolin::Handler3D(s_cam));
while (pangolin::ShouldQuit() == false)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
d_cam.Activate(s_cam);
glClearColor(1.0f,1.0f,1.0f,1.0f);
glLineWidth(2);
for(size_t i=0; i<poses.size(); i++)
{
Vector3d Ow = poses[i].translation();
Vector3d Xw = poses[i] * (0.1 * Vector3d(1,0,0));
Vector3d Yw = poses[i] * (0.1 * Vector3d(0,1,0));
Vector3d Zw = poses[i] * (0.1 * Vector3d(0,0,1));
glBegin(GL_LINES);
glColor3f(1.0,0.0,0.0);
glVertex3d(Ow[0],Ow[1],Ow[2]);
glVertex3d(Xw[0],Xw[1],Xw[2]);
glColor3f(0.0,1.0,0.0);
glVertex3d(Ow[0],Ow[1],Ow[2]);
glVertex3d(Yw[0],Yw[1],Yw[2]);
glColor3f(0.0,0.0,1.0);
glVertex3d(Ow[0],Ow[1],Ow[2]);
glVertex3d(Zw[0],Zw[1],Zw[2]);
glEnd();
}
for(size_t i=0; i<poses.size(); ++i) // 源程序多一条黑线,可能是读取范围超出了点集
{
glColor3f(0.0,0.0,0.0);
glBegin(GL_LINES);
auto p1 = poses[i-1], p2 = poses[i];
glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
glEnd();
}
pangolin::FinishFrame();
usleep(5000);
}
}
void test_play(string TrajectFile)
{
vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses;
ifstream fin(TrajectFile); // 读取坐标文件
if(!fin){
cout << "fail to open";
}
while(!fin.eof()) // 循环读取所有数据v
{
double time,tx,ty,tz,qx,qy,qz,qw;
fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
Isometry3d Twr(Quaterniond(qw,qx,qy,qz)); // +四元数
Twr.pretranslate(Vector3d(tx,ty,tz)); // +T坐标
poses.push_back(Twr); // 放到后边
}
cout << "read" << poses.size() << "poses" << endl;
DrawTrajectory(poses);
}
void DrawTrajectory2(PosesType poses1, PosesType poses2)
{
pangolin::CreateWindowAndBind("Viewer",1024,768);
glEnable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024,768,500,500,512,389,0.1,1000),
pangolin::ModelViewLookAt(0,-0.1,-1.8,0,0,0,0.0,-1.0,0.0)
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0,1.0,0.0,1.0,-1024.0f/768.0f)
.SetHandler(new pangolin::Handler3D(s_cam));
while (pangolin::ShouldQuit() == false)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
d_cam.Activate(s_cam);
glClearColor(1.0f,1.0f,1.0f,1.0f);
glLineWidth(2);
for(size_t i=0; i<poses1.size(); ++i) // 源程序多一条黑线,可能是读取范围超出了点集
{
glColor3f(0.0,127.0,0.0);
glBegin(GL_LINES);
auto p1 = poses1[i-1], p2 = poses1[i];
glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
glEnd();
}
for(size_t i=0; i<poses2.size(); ++i) // 源程序多一条黑线,可能是读取范围超出了点集
{
glColor3f(127.0,0.0,0.0);
glBegin(GL_LINES);
auto p3 = poses2[i-1], p4 = poses2[i];
glVertex3d(p3.translation()[0], p3.translation()[1], p3.translation()[2]);
glVertex3d(p4.translation()[0], p4.translation()[1], p4.translation()[2]);
glEnd();
}
pangolin::FinishFrame();
usleep(5000);
}
}
void test_play2(string TrajectFile1, string TrajectFile2)
{
vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses1;
ifstream fin1(TrajectFile1); // 读取坐标文件
if(!fin1){
cout << "fail to open";
}
while(!fin1.eof()) // 循环读取所有数据v
{
double time,tx,ty,tz,qx,qy,qz,qw;
fin1 >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
Isometry3d Twr(Quaterniond(qw,qx,qy,qz)); // +四元数
Twr.pretranslate(Vector3d(tx,ty,tz)); // +T坐标
poses1.push_back(Twr); // 放到后边
}
cout << "read" << poses1.size() << "poses" << endl;
vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses2;
ifstream fin2(TrajectFile2); // 读取坐标文件
if(!fin2){
cout << "fail to open";
}
while(!fin2.eof()) // 循环读取所有数据v
{
double time,tx,ty,tz,qx,qy,qz,qw;
fin2 >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
Isometry3d Twr(Quaterniond(qw,qx,qy,qz)); // +四元数
Twr.pretranslate(Vector3d(tx,ty,tz)); // +T坐标
poses2.push_back(Twr); // 放到后边
}
cout << "read" << poses2.size() << "poses" << endl;
DrawTrajectory2(poses1, poses2);
}
TrajectoryType ReadTrajectory(const string &path)
{
TrajectoryType trajectory;
ifstream fin(path); // 读取坐标文件
if(!fin){
cout << "fail to open";
}
while(!fin.eof()) // 循环读取所有数据v
{
double time,tx,ty,tz,qx,qy,qz,qw;
fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
Sophus::SE3d p1(Eigen::Quaterniond(qx,qy,qz,qw),Eigen::Vector3d(tx,ty,tz));
trajectory.push_back(p1); // 放到后边
}
return trajectory;
}
CMakeLists.txt
cmake_minimum_required(VERSION 3.0)
project(test_lie)
find_package(Sophus REQUIRED)
include_directories("/usr/include/eigen3")
add_executable(test_lie main.cpp)
target_link_libraries(test_lie Sophus::Sophus)
find_package(Pangolin REQUIRED)
include_directories(${Pangolin_LIBRARIES})
target_link_libraries(test_lie ${Pangolin_LIBRARIES})






















 469
469











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








