偏导数(Partial Derivative)

33.偏导数

33.1 多元变量函数

33.2 二元函数

区域的边界点构成区域的边界。
如果一个区域完全由内部点组成，那么该区域就是开放的。
如果一个区域包含了它所有的边界点，那么它就是封闭的。

33.2.1 二元函数的等位曲线、等高曲线

平面上一个函数 $ƒ(x,y)$ 具有一个常数值 $ƒ(x,y)=c$ 的点集称为 $ƒ$ 的等位曲线。
空间中所有点 $(x,y，ƒ(x,y))$ 的集合，对于ƒ定义域中的 $(x,y)$，称为 $ƒ$ 的图。$ƒ$ 的图形也称为曲面 $z=ƒ(x,y)$。

33.3 三元函数

33.3.1 三元函数的等位曲面

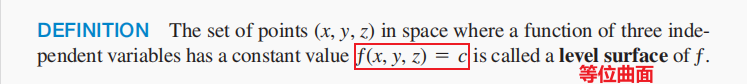
33.4 高维函数中极限与连续性

33.4.1 二元函数的极限

两变量函数极限的性质

求极限的例子：
例1：

例2：

例3：

圆柱的半径取 $\delta$、$z=ϵ$、$z=-ϵ$

33.4.2 二元函数的连续性

例子：

点$(0,0)$处的极限值不等于函数值，所以该函数在点$(0,0)$处不连续

极限不存在性的双路检验

例子：

33.5 偏导数

当我们保持一个函数常数中除一个自变量外的所有自变量并对这一个变量求导时，我们得到一个“偏”导数

单一变量函数中对某个变量的微分用符号 “$d$” 表示
多元变量函数中对某一变量的微分（即偏导）我们用符号 “$\partial$"

33.5.1 二元函数的偏导数

33.5.1.1 函数在某点处对变量 x 进行偏导

函数 $f(x,y)$ 在点 $(x_0,y_0)$ 处对变量 $x$ 的偏导数
（变量 $x$、应变量 $z$、常数 $y$）

33.5.1.2 函数在某点处对变量 y 进行偏导

函数 $f(x,y)$ 在点 $(x_0,y_0)$ 处对变量 $y$ 的偏导数
（变量 $y$、应变量 $z$、常数 $x$）

例子：

33.5.2 二阶偏导数

混合偏导定理

33.6 链式法则

33.6.1 一个自变量、一个中间变量的函数的链式法则

33.6.2 一个自变量、两个中间变量的函数的链式法则

33.6.3 一个自变量、三个中间变量的函数的链式法则

33.6.4 两个自变量、三个中间变量的函数的链式法则

33.6.5 隐函数的导数

例子：