信噪比SNR = 6.02N + 1.76dB

1、量化噪声模型

1.1、量化噪声模型

        理想转换器对信号进行数字化时，最大误差为±½ LSB，如图1的一个理想N位ADC的传递函数所示。对于任何横跨数个LSB的交流信号，其量化误差可以通过一个峰峰值幅度为q(一个LSB的权重)的非相关锯齿波形来近似计算。对该近似法还可以从另一个角度来看待，即实际量化误差发生在±½ q范围内任意一点的概率相等。虽然这种分析不是百分之百精确，但对大多数应用是足够准确的。

图1 理想N位ADC的量化噪声

        图2更详细地显示了量化误差与时间的关系。同样，一个简单的锯齿波形就能提供足够准确的分析模型。锯齿误差的计算公式如下：

e(t) = st, –q/2s < t < +q/2s（电压与时间的关系）

        e(t)的均方值可以表示为：（功率）

        进行简单的积分和简化可得：

        因此，均方根量化误差为：

图2：量化噪声与时间的关系

        锯齿误差波形产生的谐波远远超过DC至fs/2的奈奎斯特带宽，然而，所有这些高阶谐波必须折回(混叠)到奈奎斯特带宽并相加，产生q/√12的均方根噪声。

        量化噪声近似于高斯分布，几乎均匀地分布于从DC至fs/2的奈奎斯特带宽。这里假设量化噪声与输入信号不相关。在某些条件下，当采样时钟和信号通过谐波相关时，量化噪声将与输入信号相关，能量集中在信号的谐波中，但均方根值仍然约为q/√12。理论信噪比现在可以通过一个满量程输入正弦波来计算：
 

因此，输入信号的均方根值为：
 

因此，理想N位转换器的均方根信噪比为：

        虽然量化噪声的实际频谱相当复杂，难以分析，但推导出等式（SNR = 6.02N + 1.76dB, DC至fs/2带宽范围）的简化分析对大多数应用足够准确。然而，必须再次强调，均方根量化噪声是在DC至fs/2的完整奈奎斯特带宽范围内进行测量。

1.2、过/欠采样量化噪声模型

        许多应用中，实际目标信号占用的带宽BW小于奈奎斯特带宽（fs/2），参见图3。

图3：显示处理增益的量化噪声频谱
 

        如果使用数字滤波来滤除带宽BW以外的噪声成分，则等式中必须包括一个校正系数(称为“处理增益”)，以反映SNR的最终提高（过采样能提高信噪比），如下述等式所示。

        以两倍以上的信号带宽的速率对信号进行采样的过程称为“过采样”。过采样、量化噪声整形和数字滤波均是Σ-Δ型转换器的重要概念，不过任何ADC架构都可以采用过采样技术。

        处理增益的意义可以通过下例说明。

        在许多数字基站或其它宽带接收机中，信号带宽由许多独立的通道组成，一个ADC对整个带宽进行数字化处理。例如，美国的模拟蜂窝无线电系统(AMPS)由416个30 kHz带宽通道组成，占用的带宽约为12.5 MHz。假设采样速率为65 MSPS，并且使用数字滤波来分离各个30 kHz通道。在这些条件下，过采样导致的处理增益为：

        将处理增益加入ADC SNR规格，便得到30 kHz带宽内的SNR。上例中，如果ADC SNR规格
为65 dB(DC至fs/2)，则30 kHz通道带宽内的SNR提高到95.3 dB(经过适当的数字滤波后)。

        图4显示了一个结合过采样和欠采样（位于第二奈奎斯特区间）的应用。目标信号的带宽为BW，以载波频率fc为中心。采样频率可以远低于fc，所选的采样频率使得目标信号位于其奈奎斯特区的中心。通过模拟和数字滤波消除目标信号带宽以外的噪声，从而获得等式10所示的处理增益。

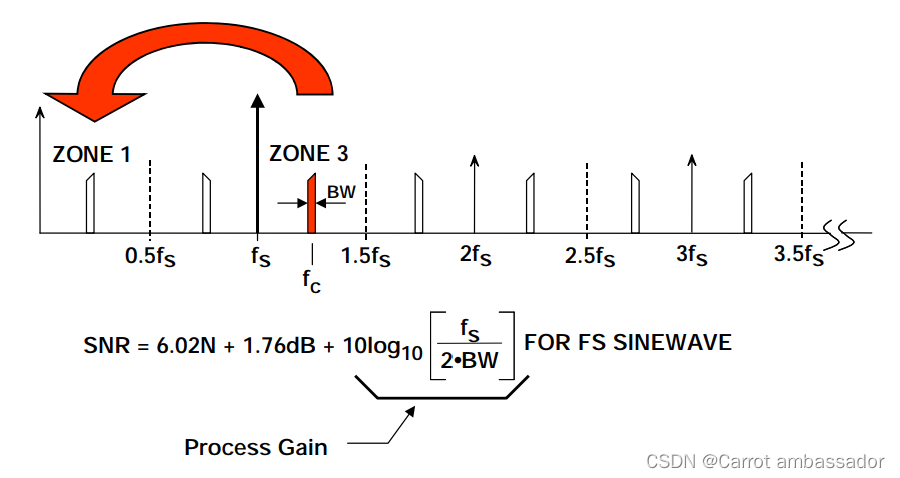
图4：欠采样和过采样结合所产生的处理增益

2、量化噪声与输入信号之间的相关性

        虽然噪声的均方根值可通过q/√12计算精确近似值，但在某些条件下，频域成分可能与交流输入信号高度相关。例如，低幅度周期性信号的相关度大于高幅度随机信号的相关度。通常假设理论量化噪声表现为白噪声，均匀地分布在DC至fs/2的奈奎斯特带宽范围。但是，事实并非全然如此。在强相关的情况下，量化噪声集中在输入信号的各次谐波上，这正是我们不希望看到的。
        在多数实际应用中， ADC的输入是一段频率(总是会与一些不可避免的系统噪声相加)，因此量化噪声往往是随机的。然而，在频谱分析应用中(或者使用频谱纯净的正弦波作为输入对ADC执行FFT)，量化噪声与信号的相关度取决于采样频率与输入信号的比值。
        图5的示例说明了这种情况，其中使用一个4096点FFT来分析一个理想12位ADC的输出。在左边的FFT图(A)中，采样频率(80.000 MSPS)与输入频率(2.000 MHz)的比值恰好选择为40，最差谐波比基波低大约77 dBc。右图(B)显示了将输入频率略微偏移到2.111 MHz的效果，表现出随机性相对较高的噪声频谱，此时SFDR约为93 dBc，受FFT噪底尖峰限制。两种情况下，所有噪声成分的均方根值均近似于q/√12(理论SNR因此为74 dB)，但在第一种情况下，噪声因为相关性而集中在基波谐波上。

图5：采样时钟与输入频率的比值对理想12位ADC量化噪声频谱的影响， 4096点FFT
(A) 相关噪声， (B) 非相关噪声

         注意，从ADC看到的谐波失真的这种变化是采样过程的伪像，由量化误差与输入频率的相关性引起。在实际ADC应用中，量化误差一般表现为随机噪声，原因是宽带输入信号具有随机性，而且通常会有少量的系统噪声充当“扰动”信号，使量化误差频谱进一步随机化。理解上述原理非常重要，因为ADC的单音正弦波FFT测试是公认的性能评估方法之一。为了精确测量ADC的谐波失真，必须采取措施确保测试设置能够真正测量ADC失真，而不是量化噪声相关性引起的伪像。因此，必须正确选择频率比，有时还要将少量噪声（扰动）与输入信号相加。利用模拟频谱分析仪测量DAC失真时，也应采取同样的防范措施。

3、SNR、处理增益和FFT噪底的关系。

        图6显示了一个理想12位ADC的FFT输出。注意， FFT噪底的平均值约为满量程以下107dB，但12位ADC的理论SNR为74 dB（SNR=6.02N+1.76dB=6.02x12+1.76）。 FFT噪底并非ADC的SNR，因为FFT像是一个带宽为fs/M的模拟频谱分析仪，其中M为FFT中的点数。由于FFT的处理增益，理论FFT噪底因而比量化噪底低10log10(M/2) dB。
        对于SNR为74 dB的理想12位ADC， 4096点FFT将产生10log10(4096/2) = 33 dB的处理增益，因此总FFT噪底为74 + 33 = 107 dBc。事实上， FFT噪底可以通过提高FFT点数来进一步降低，就像模拟频谱分析仪的噪底可以通过缩小带宽来降低一样。因此，利用FFT测试ADC时，必须确保FFT足够大，使得失真能够与FFT噪底本身区别开。多次FFT的平均值无法进一步降低噪底，只能减小各个噪声谱成分幅度之间的差异。

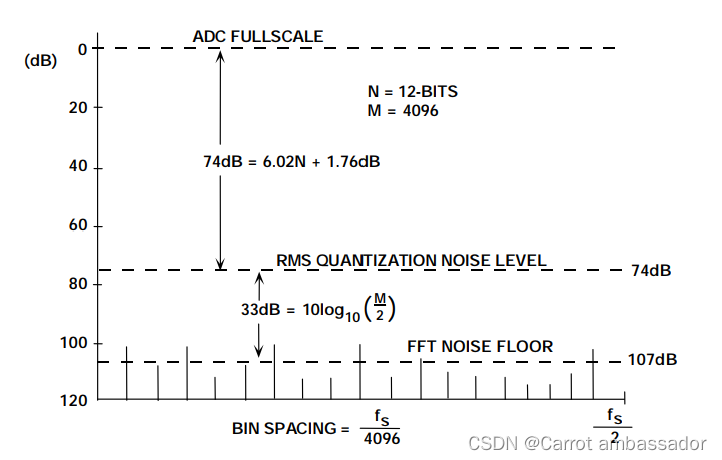
图6：理想12位ADC的噪底，使用4096点FFT
 

--内容来源 ADI《MT-001揭开一个公式(SNR = 6.02N + 1.76dB)的神秘面纱》