【人工智能】天工开悟系列 1：词源逻辑性约束与算法约束

一、背景：逻辑理论

逻辑概念：
1.字本位
汉字独立性约束​：
基于汉字作为基本语义单元的特性，构建字形-语义联合空间。
因汉语中的字、词元、谚语、术语、诗词等多样性较大，需要设计前导性的分类系统进行提前的输入，避免直接混合训练(可以参考汉语词典、成语词典、百家姓等主要的基础系统进行初始化学习）

其中ϕ shape
为笔画结构编码器（如基于CNN的汉字骨架提取），ϕ semantic为BERT类语义编码器。验证时需满足

通过余弦相似度度量输出字符与标准字库的匹配度（汉字表意特征）

​组合规则约束​
采用双向有限状态机（FSA）验证汉字组合的合法性

其中G compose为预定义的汉字组合语法图（如部首搭配规则），通过CRF模型实现转移概率计算（汉字多义性分析）。
此时需要分简体汉字、繁体字、甲骨文等古文体系不同字体系列的部首配置要求。

2.递归性
​递归结构检测​
对模型输出的语法树进行结构递归性分析

其中≅ iso表示子树与整体结构的同构关系。通过Z3求解器验证语法树是否存在自相似子结构（递归模式定义）

​递归神经网络的形式化​
对RNN/LSTM隐藏状态进行数学建模：

需证明其满足递归收敛性条件：

通过Lipschitz常数约束保证状态传递的稳定性（递归边界条件）

3.定义性
一阶逻辑约束注入​
将领域知识转化为谓词逻辑规则，例如数学公式的运算符优先级

通过模型检查工具（如TLA+）验证输出是否满足所有约束。

动态类型系统验证​
构建类型推导的递归函数：

通过类型一致性检查（Type Consistency Check, TCC）确保表达式符合运算规则（引入算术表达式解析）

结合多种特征进行综合验证

1. 联合验证模型
   构建多目标优化函数整合三类约束：
   
   其中：
   

2. 符号执行与模型检查
   使用Angr等工具遍历模型输出路径：
   
   确保所有可能输出路径均满足定义性约束（符号执行方法）。

---

逻辑特征：

1.导向性
人文伦理导向性​
构建伦理规则库与逻辑约束项，通过正则化项约束模型输出方向：

其中，Φ(e i )为模型输出伦理向量，Ψ(e i )为伦理规则库中标准向量（如生物伦理中的基因编辑边界规则）。通过对比语义空间中的向量距离，确保输出符合人文价值导向。
数学逻辑导向性​
引入谓词逻辑与代数约束，验证输出是否符合数学公理体系：
​命题逻辑验证​：若模型输出命题P，需满足∀x(P(x)→Q(x))，其中Q(x)为数学公理库中的约束条件（如群论封闭性）。
​动态规划验证​：对于路径规划类输出，需满足贝尔曼方程约束

---

2.质疑性

1. 物理工程冲突检测
   通过守恒定律与动力学方程验证输出合理性：
   • 经典物理验证：动量守恒方程约束：
     
   • 量子物理验证：波函数归一化条件：

2. 化学与生物质疑机制

   • 反应动力学验证：质量作用定律约束速率方程：
     

   • 基因频率验证：哈迪-温伯格定律约束：
     

---

3.判断性

1. 数学方程驱动的推理链
   构建可微分逻辑推理网络，融合一阶逻辑与张量运算：
   
   其中(\mathbf{v}_i)为实体向量，(\mathbf{r}_i)为关系矩阵，(\mathbf{c}_i)为化学/生物属性向量（如分子键能、细胞代谢路径）。
   2. 溯因推理与假设检验
   结合最小假设集理论与贝叶斯推断，验证输出逻辑自洽性：
   
   其中(K)为跨学科知识库（如物理守恒律+化学平衡方程+生物种群模型）。

---

人文科学方面，需要考虑交叉验证、溯因推理、伦理约束等。可采用逆向提问法和异常点追踪，可以用于质疑性验证。伦理约束可能需要构建伦理规则库，置信度阈值和伦理过滤层，可能相关。
数学方程方面，可以用到概率模型、逻辑约束等。采用交叉验证和超参数调优，以及残差分析和灵敏度分析，将其转化为数学表达式和对应的测算方程。引入MERML模型中的递归算法和多重估计策略，对判断性预计有帮助。
在物理学的约束方面，可以引用物性模型验证中的守恒定律嵌入，比如动量守恒方程，可以用于物理一致性检验。至于线性方程组在模型验证中的应用，可能涉及到动力学方程的约束。化学动力学建模，比如速率方程和反应网络微分方程组，可以用于验证化学反应预测的合理性。递归动力学模型可能是一个例子，结合了数据驱动和物理方程。

1. 多目标优化框架
   构建联合损失函数整合多学科约束：
   
   各学科损失项分别对应伦理规则冲突、物理守恒误差、化学反应速率偏差、生物遗传频率异常。

评估体系与指标​
​跨学科一致性指数​
综合多领域专家评估结果，量化模型输出与学科共识的偏离度
​可解释性增强技术​
​注意力可视化​：通过Grad-CAM展示模型决策关键区域；
​逻辑规则提取​：使用LIME生成局部可解释规则

2. 动态调度与异构验证
   设计分阶段验证流程：
   • 符号执行阶段：调用求解器验证数学逻辑约束；
   • 数值验证阶段：通过有限元分析（FEA）验证物理工程一致性；
   • 生化仿真阶段：使用COPASI等工具模拟化学反应网络动态。

• 基因编辑模型验证*
  • 导向性：CRISPR靶点选择需满足(\text{Off-target Score} < 0.2)（伦理约束）；
  • 质疑性：通过qPCR实验数据验证编辑效率是否符合动力学方程(E = E_{\max} \cdot (1 - e^{-kt}))；
  • 判断性：基于SNP分布验证是否符合哈迪-温伯格平衡。

量子计算输出验证

• 导向性：量子线路设计需满足拓扑编码规则（如表面码逻辑门约束）；
• 质疑性：通过量子态层析验证输出态保真度(F = \text{Tr}(\rho_{\text{ideal}} \rho_{\text{output}}))；
• 判断性：验证Shor算法分解结果是否满足(N = p \times q)（数论公理）。

---

逻辑类别：
1.自证性
2.互证性
3.它证性

---

逻辑的思想：
1.确定性
2.预期性
3.保障性

---

逻辑的程序：
1.选择性
2.因果性
3.实践性

---

逻辑的样式：
1.目标性
2.命题性
3.语境性

---

逻辑的原因：
1.论证性
2.实证性
3.验证性

---

逻辑的目的：
1.描绘性
2.优化性
3.解释性

---

逻辑的功能：
1.陈述性
2.描述性
3.阐述性

---

逻辑的思想：
1.对称性
2.规范性
3.关联性

---

逻辑的规律：
1.同一性
2.不矛盾律
3.排中律

---

逻辑的样式：
1.证明性
2.证实性
3.证据性

---

逻辑的思辨：
1.归纳性
2.综合性性
3.演绎性

---

逻辑的抽象：
1.针对性
2.提练性
3.纯粹性

---

逻辑的理论价值：
1.条例性
2.可读性
3.学术性

---

不同逻辑系统及其数学表达式的综合分析

一阶逻辑与二阶逻辑

1. 一阶逻辑（First-Order Logic, FOL）

   • 定义与核心特征：
     一阶逻辑通过量词（∀、∃）对个体变量进行量化，描述对象之间的关系。其基本表达式为原子命题的复合形式，例如：
     
     表示“所有满足性质( P )的对象都满足性质( Q )”。
   • 数学表达式示例：
     • 命题形式：( \exists x (Human(x) \land Mortal(x)) )（存在人类且会死亡的对象）。
     • 局限性：无法直接量化谓词或函数，如“所有性质都满足某个条件”无法表达。

2. 二阶逻辑（Second-Order Logic, SOL）

   • 定义与扩展能力：
     二阶逻辑允许对谓词和函数进行量化，增强表达能力。例如：
     
     表示“存在一个性质( P )，与性质( Q )相反”。

   • 应用场景：

     • 描述数学公理（如实数的最小上界性质）；
     • 表达复杂关系（如“所有对称关系都满足某种条件”）。

   • 与一阶逻辑的对比：

     特征	一阶逻辑	二阶逻辑
     量化对象	个体变量	个体、谓词、函数
     可判定性	递归可枚举	不可判定
     表达能力	有限	更强（如集合论）

---

高阶逻辑与多阶逻辑

1. 三阶及以上逻辑

   • 三阶逻辑允许量化“谓词的集合”，例如描述“所有可能的性质集合满足某种规则”。
   • 数学表达式示例：
     [
     \forall \mathcal{P} (\exists x \mathcal{P}(x) \rightarrow \exists y \mathcal{P}(y))
     ]
     表示“若某类性质非空，则存在对象满足该类性质”。

2. 多阶逻辑（Higher-Order Logic, HOL）

   • 将量化层次扩展至任意阶数，适用于数学基础研究（如范畴论中的抽象结构）。
   • 特点：
     • 通过类型系统分层（个体类型、谓词类型等）；
     • 在定理证明工具（如HOL Light）中广泛应用。

---

主从逻辑与群体逻辑

1. 主从逻辑（Master-Slave Logic）

   • 定义：分布式系统中的任务分工模型，主节点负责协调，从节点执行子任务。
   • 数学表达式示例：
     • 任务分配：( \text{Master}(T) \rightarrow \bigwedge_{i=1}^n \text{Slave}(T_i) )（主节点将任务( T )分解为( T_1, \dots, T_n )分配至从节点）。
   • 应用：
     • 数据库主从复制（主节点权威，从节点同步）；
     • 分布式计算（如MapReduce框架）。

2. 群体逻辑（Swarm Logic）

   • 定义：描述多主体协同行为的逻辑系统，常用于群体智能（如蚁群算法）。
   • 核心模型：
     • 基于局部规则：( \forall a \in \text{Agent}, \exists R(a) \rightarrow \text{Action}(a) )，表示“每个主体根据局部规则( R )行动”；
     • 全局涌现：通过个体交互产生集体行为模式（如路径优化）。

方法理论与数学工具

1. 逻辑推理方法

   • 归纳与演绎：
     • 数学归纳法：验证基础情况并递推（如证明( \sum_{i=1}^n i = \frac{n(n+1)}{2} )）；
     • 反证法：假设结论不成立导出矛盾（如证明( \sqrt{2} )为无理数）。

2. 形式化建模工具

   • 模态逻辑：引入模态算子（如必然性( \Box )、可能性( \Diamond )），用于知识表示与时态推理。
   • 数字电路逻辑：
     • 基本运算：与（( A \land B )）、或（( A \lor B )）、非（( \neg A )）；
     • 复合逻辑：异或（( A \oplus B = \neg A \cdot B + A \cdot \neg B )）。

综合应用与前沿方向

1. 跨领域融合

   • 神经符号系统：结合神经网络的感知能力与符号逻辑的推理能力，例如将知识图谱规则注入损失函数。
   • 量子逻辑：探索量子计算中的非经典逻辑（如量子纠缠态的逻辑表达）。

2. 挑战与优化

   • 可扩展性：高阶逻辑的推理复杂度需依赖异构计算加速；
   • 伦理约束：在群体逻辑中嵌入公平性规则（如避免算法歧视）。

---

总结

不同逻辑系统通过量化层次、对象类型及推理方法的差异，构建了从基础数学到分布式计算的完整理论框架。

通过逻辑学相关理论对AI输出结果进行重新归纳

归结原理与子句集重构

1. 归结式生成算法
   通过互补文字消解生成新子句，实现逻辑矛盾检测与结果简化。其核心表达式为：
   

   其中( C_1 )和( C_2 )为原子子句，( L )为互补文字（如( A )与( \neg A )）。通过反复应用此规则，可将AI输出（如分类结果或文本推理）转化为无矛盾子句集。
   应用示例：在医疗诊断中，若AI输出“症状S→疾病D”与“症状S→非疾病D”矛盾，通过归结可推导空子句（矛盾），触发规则修正。

2. 子句集标准化流程
   将非结构化输出转化为合取范式（CNF）以支持自动推理：

其中( L_{ij} )为原子文字或否定文字，适用于自然语言处理中的命题抽取。

---

归纳逻辑编程（ILP）规则提取

1. 假设空间搜索算法
   通过最小描述长度原则生成逻辑规则：
   

   其中( H )为假设规则集，( D )为AI输出数据集，( \lambda )为复杂度惩罚系数。

2. 一阶逻辑增强表示
   使用谓词逻辑描述复杂关系：
   
   此类表达式可将风控模型的二分类结果转化为可解释的审计规则。

---

逻辑回归与概率约束融合

1. 带逻辑约束的损失函数
   在标准交叉熵损失中注入领域知识：
   

   其中( p_i = \sigma(\theta^T x_i) )为Sigmoid输出，( \gamma )控制逻辑先验的约束强度。
   应用示例：在信用评分中强制“年龄<18→拒绝”的硬规则。

2. 模糊逻辑扩展
   引入隶属度函数处理不确定推理：
   
   结合AI输出的概率值，实现“紧急邮件”的动态阈值判定。

---

溯因推理框架

1. 多目标优化模型
   结合逻辑一致性与数据拟合度：
   

   其中( K )为领域知识库，( \alpha )平衡假设成本与逻辑冲突。

2. 动态知识库更新
   通过增量式规则学习保持逻辑系统进化：
   
   例如支持自动驾驶场景中新增交通规则的在线整合。
   –

扩展

可通过逻辑约束注入、规则自动生成和动态知识演化三大机制，将AI的原始输出转化为符合领域逻辑的结构化知识。未来可探索：

1. 量子逻辑门集成：用量子并行性加速大规模子句归结；
2. 神经符号混合架构：如Transformer+Problog实现可微分逻辑推理；
3. 伦理约束自动化验证：通过模态逻辑检测歧视性规则。

实际部署时需根据任务类型选择方法——硬逻辑约束（如医疗诊断）适合归结原理，软规则学习（如推荐系统）倾向ILP，而动态环境（如机器人导航）需结合溯因推理。

二、中文语境的词源

2.1、逻辑性约束

1. 词源理据与语义关联
   汉语词的理据（motivation）体现了形式与意义的内在联系，例如部分汉语文字通过同源词和方言材料验证其语义关联。这种逻辑性约束强调词语的构成部分与整体意义的必然性联系，如复合词的内部形式（语法和语义结构）需通过理据揭示。
   此外，外来词选择时优先考虑字义联想性（如“基因”暗示“基本因子”）或相关性（如“葡萄”从“艹”），而非单纯追求语音相似性。

2. 语言结构特性
   汉语的主谓结构不分明，缺乏系词（如“to be”），导致逻辑命题的构建不同于印欧语系。例如，“仁者人也”中“者”和“也”并非系词，而是语助词，使得词与句的语义关系更依赖上下文而非显性语法标记。这种特性强化了汉语的“意合”特征，即语义组合依赖概念或情境关系，而非形式规则。

3. 分析型语言特征
   汉语形态不发达，语法化程度低，句法关系多通过词汇和语序实现。例如，动词隐含的主宾语常省略，但对语义类型匹配度要求较高，导致事件强迫机制（如“赶论文”隐含“写”）需依赖语义推理。这种分析性特征使得词源逻辑更多体现为语义网络的自由组合，而非形态标记的强制约束。

4. 外来词选择的层级约束
   外来词词形选择的制约条件呈等级序列：字形俗成性 > 字义相关性/联想性 > 语音相似性 > 书写经济性。例如，“可口可乐”虽语音偏离原词，但字义联想更优。

---

2.2、运筹规划约束

运筹科学经常用于解决现实生活中的复杂问题，特别是改善或优化现有系统的效率。 研究运筹学的基础知识包括实分析、矩阵论、随机过程、离散数学和算法基础等。

2.3、算法

1. 分词与歧义消解
   中文分词依赖词典约束法（匹配预定义词汇）和优先级判断法（高频词优先），结合统计模型（如互信息）衡量词语内部结合紧密度。例如，基于语义构词约束的算法通过隐马尔可夫模型（HMM）和语义转移概率矩阵，增强同主题词语的内聚性，减少歧义。深度学习方法（如LSTM、Transformer）进一步捕捉复杂语义关系，提升低频词识别能力。

2. 语义约束的模型优化
   在主题模型中引入语义约束机制（如SRC-LDA），通过**MSG（语义相关组）和CSG（语义冲突组）**调整主题-词语分配概率，增强特征词和情感词的一致性。例如，同一主题下增强MSG词语的分布概率，抑制CSG词语的耦合性，从而提取细粒度语义特征。

3. 动态资源与规则融合
   算法需平衡显性规则（如词典）与动态学习（如语料库统计）。例如，基于生成词库理论的模型结合物性结构（qualia structure）和类型强迫机制，协调形义错配问题，如隐含谓词的语义角色推断。同时，弹性资源分配机制可根据实时请求调整预填充与解码节点资源，提升效率。

---

2.4、逻辑与算法的交互关系

1. 逻辑性约束驱动算法设计
   汉语的意合特征要求算法更依赖语义网络而非语法规则。例如，分词算法需结合语义构词约束（如“俄军”通过“国家+军队”模式推断为词），而主题模型需通过语义相关性优化主题聚类。

2. 算法技术弥补逻辑性不足
   汉语形态和语法的隐含性需算法通过上下文建模弥补。例如，LSTM捕捉长距离依赖解决主谓省略问题，而SRC-LDA通过语义约束增强低频词识别。

---

总结

中文词源的逻辑性约束植根于其语义优先、意合主导的语言特性，而算法约束则通过统计学习、语义模型和动态优化应对这些特性带来的挑战。二者共同作用，推动中文自然语言处理技术在分词、歧义消解、主题挖掘等任务中的精准性和适应性。后续可以聚焦于多模态语义融合（结合图像、语音）和跨语言逻辑迁移（如中英文混合模型）。

三、英文语境的词源

3.1、词源逻辑性约束

1. 词源演化与多义性
   英语词汇的语义扩展往往源于核心概念的延伸。例如，“discipline"既表示“纪律”又表示“学科”，其词源可追溯至拉丁语"disciplina”（教导与知识），反映了教育过程中秩序约束与知识体系的统一性。类似地，“revenue”（收入）源自拉丁语"re-“（回）与"venire”（来），隐含“付出后回流”的经济逻辑。这类词源逻辑要求算法需理解历史语义关联，避免割裂多义性。

2. 专业术语的固化逻辑
   法律、商务等领域的专业术语（如"hereof", “notwithstanding”）多源于中古英语或拉丁语，通过长期判例法形成固定用法。例如，英文合同中"it"严格指代前文最后一个名词，避免歧义。这种逻辑性约束要求算法需内置领域词典及语法规则库，以识别特定语境下的语义指向。

3. 构词法的系统性
   词缀与词根组合遵循明确逻辑。例如：

   • “circumvent”（绕过）= “circum”（环绕） + “vent”（走）；
   • “intervene”（干预）= “inter”（中间） + “vene”（来）。
     此类构词规律可指导算法进行词义分解与生成，例如通过词缀树模型预测未登录词含义。

---

3.2、算法约束

1. 上下文消歧与语义建模
   多义词的义项选择高度依赖语境。例如介词"on"在词典中有10+义项，但实际使用中仅需基于上下文激活单一语义。算法需结合注意力机制（如Transformer）捕捉局部语境，或通过预训练语言模型（如BERT）生成动态词向量。

2. 句法与语义的联合约束
   空白填充任务需同时满足语法规则（如主谓一致）和语义连贯性。例如：

   • 句子"The car was red.“中，“red"可替换为"crimson”，但不可用"run”；
   • 复合句嵌套结构需遵循子集原则，禁止不合逻辑的从句插入。
     算法需集成句法解析器（如Stanford Parser）与语义角色标注（SRL），确保生成内容符合双重约束。

3. 领域适应性优化
   不同语域（如法律、医学）对词汇选择有严格限制。例如：

   • 法律文本偏好"terminate"而非"finish"表示终止；
   • 医学文献要求精确使用专业术语（如"myocardial infarction"而非"heart attack"）。
     算法需通过领域适配技术（如Domain-Specific Fine-tuning）调整词表权重，或构建多任务学习框架分离通用与专用语义。

---

3.3、逻辑与算法的交互优化

1. 规则注入与统计学习的平衡
   传统方法依赖显式规则（如词典匹配），但难以覆盖语言动态性。现代模型（如SRC-LDA）将语义约束组（MSG）融入主题模型，通过概率分布抑制不合理词项组合。例如，在生物医学文本中增强"gene"与"DNA"的共现概率，抑制"gene"与"cooking"的关联。

2. 跨语言逻辑迁移
   英语的意合特征（如省略主谓）与汉语结构差异显著。算法需通过对比学习（Contrastive Learning）捕捉跨语言逻辑差异，例如中英混合模型中分离语法树生成路径。

3. 动态资源分配
   实时语境变化要求算法弹性调整资源。例如：

   • 在对话系统中，根据用户意图动态切换正式/非正式语域词库；
   • 长文本处理时，通过记忆网络（Memory Networks）保留关键实体指代关系，避免逻辑断裂。

---

3.4、挑战与前沿方向

1. 历史词源与当代用法的冲突
   部分古英语词项（如"thou"）已脱离现代语境，但文学文本仍需保留其原义。算法需构建时间感知嵌入（Temporal Embedding）区分历时语义。

2. 低资源领域的泛化能力
   专业领域（如法律拉丁语）数据稀缺，需通过元学习（Meta-Learning）快速适配，或利用知识图谱补全术语逻辑链。

3. 伦理与文化敏感性
   词汇可能隐含冒犯性（如种族歧视术语），算法需集成伦理过滤层，结合文化约束规则自动检测并替换。

---

英文词源的逻辑性约束根植于历史演变、专业固化与构词系统性，而算法约束需通过上下文建模、多模态学习与动态优化应对这些特性。

四、数学符号的复杂起源与多重约束分析

数学符号作为数学思想的“压缩算法”，其发展历程融合了人类文明的抽象化进程、跨文化互动与逻辑严密性需求。以下从起源、算法约束、逻辑约束及相关性约束四个维度展开分析：

---

4.1、起源：符号的跨文化融合与历史演变

1. 运算符号的全球化路径

   • 加减号（+、-）：15世纪德国数学家魏德曼从拉丁文“et”（和）与“minus”（减）演变而来，最初用于商业账目标记，后经印刷术推广成为国际标准。
   • 乘号（×、·）：英国数学家奥屈特1631年提出“×”，而“·”由赫锐奥特首创，莱布尼茨为避免与字母X混淆支持后者，最终两种符号并存。
   • 除号（÷）：瑞士数学家拉哈在《代数学》中正式引入，其形态源于中世纪欧洲的减号与分数线的结合。

2. 关系符号的逻辑固化

   • 等号（=）：1557年英国数学家列考尔德以两条平行线象征相等，终结了“aequalis”等冗长表述，成为逻辑一致性的基石。
   • 不等号（>、<）：1631年英国代数学家赫锐奥特首创，通过符号形态直接映射量的大小关系。

3. 特殊常数的符号化突破

   • 圆周率π：1706年威廉·琼斯首次用希腊字母π表示，欧拉推广后成为标准，其符号选择兼顾几何直观与文化象征。
   • 自然常数e：欧拉在研究指数函数时命名，符号简洁性与其在微积分中的核心地位相匹配。

---

4.2、算法约束：符号处理的标准化与歧义消解

1. 符号系统的机器可读性优化

   • 20世纪ISO 80000规范统一符号（如∈、∪、∫），使数学表达可被计算机解析，例如集合论符号∈的严格定义避免算法中的逻辑漏洞。
   • 微积分符号（dx/dy、∫）的莱布尼茨体系因其可操作性成为数值计算与符号演算的基础。

2. 多义性与上下文依赖

   • 符号“·”既表示乘法（标量积）又表示点积（矢量运算），算法需结合数据类型动态解析。
   • 根号“√”的运算优先级在代数与几何中差异显著，需通过语法树约束避免歧义。

---

4.3、逻辑约束：符号与数学公理的一致性

1. 符号的语义自洽性

   • 等号（=）必须满足自反性、对称性、传递性，任何算法实现均需遵循这三条公理。
   • 集合符号（⊆、∩）的定义严格遵循ZFC公理体系，例如空集符号∅的引入避免罗素悖论。

2. 符号的形式化证明需求

   • 弗雷格引入量词符号（∀、∃）后，数学命题的证明必须通过谓词逻辑规则展开，符号成为严谨性的载体。
   • 希尔伯特形式系统将公理符号化，例如“→”表示蕴含关系时需符合分离规则（Modus Ponens）。

---

4.4、相关性约束：符号的跨领域协同

1. 符号的学科渗透

   • 布尔代数符号（∧、∨）从逻辑学扩展到计算机电路设计，其形态简洁性降低跨学科认知成本。
   • 希腊字母（Σ、Δ）在统计学（方差）、物理学（差值）中的复用，增强学科间的概念关联。

2. 历史符号的现代适应性

   • 莱布尼茨积分符号∫在量子力学中被扩展为路径积分，符号形态保留而语义深化。
   • 集合论符号（ℵ、ω）通过哥德尔不完备定理重构数学基础，符号系统需兼容经典与创新。

---

符号演化的核心动力

1. 文化动力：符号的起源反映文明交流（如阿拉伯数字的全球化）与实用需求（商业记账催生加减号）。
2. 逻辑动力：公理化运动推动符号标准化，确保数学体系的严谨性。
3. 技术动力：计算机科学要求符号可解析、无歧义，倒逼符号系统优化。
   未来，数学符号可能进一步融合人工智能的符号推理（如神经符号系统），在保持逻辑约束的同时增强算法适应性。这一进程将延续符号作为“思想压缩工具”的本质，持续推动数学与技术的协同进化。

4.5、考虑因素

1. 架构融合方式

   • 神经与符号模块的交互层级：分为神经主导（符号辅助）、符号主导（神经辅助）及平等融合三类。神经模块处理感知数据（如图像特征提取），符号模块执行逻辑推理。
   • 模块化设计：包含神经表征模块（编码输入数据为向量）、符号转换模块（向量→符号映射）、符号推理引擎（基于知识库的逻辑操作）及反馈机制（优化神经参数）。

2. 知识整合机制

   • 规则注入：通过逻辑约束（如正则化项）将符号知识嵌入神经网络训练过程，例如将知识图谱的多元组规则转化为损失函数中的约束项。
   • 动态知识更新：支持在线学习与符号规则编辑，例如通过增量式逻辑归纳（ILP）从数据中自动生成新规则。

3. 推理效率与可扩展性

   • 计算异构性：需平衡神经计算（高并行矩阵运算）与符号推理（序列化逻辑操作）的资源分配。例如，CogSys框架通过算法-硬件协同设计优化循环卷积等符号操作。
   • 内存优化：因式分解技术减少符号知识库的存储开销（如分解符号向量为低秩矩阵）。

4. 可解释性与泛化能力

   • 符号接地（Symbol Grounding）：确保符号与神经表征的语义一致性，例如通过注意力机制对齐文本符号与视觉特征。
   • 推理过程可视化：记录神经输出到符号推理的中间步骤，例如生成逻辑规则应用链的可视化报告。

---

4.6、算法表达式

1. 神经-符号混合模型
   • 神经符号张量网络：将符号逻辑嵌入张量运算.
     -例如用张量乘积表示逻辑规则：
     
     其中(\mathbf{v}_i)为实体向量，(\mathbf{r}_i)为关系矩阵，支持一阶谓词逻辑推理。

---

• 概率逻辑模型：结合马尔可夫逻辑网络（MLN）与神经网络，势函数由神经网络学习：
  
  其中(f_i(X))为神经网络输出的特征函数，(w_i)为规则权重。

---

2. 符号推理算法
   • 逻辑规则引擎：基于Drools或自定义推理机执行命题逻辑/谓词逻辑推导，例如：
     
     结合神经输出置信度调整规则触发阈值。

---

• 溯因推理（Abduction）：通过最小假设集解释观测数据，例如：
  
  其中(K)为知识库，(O)为观测数据，(H)为假设集合。
  溯因推理（Abduction）作为一种跨学科的逻辑推理方法，需整合多领域规律（如利益链、物理/化学方程、生物规律）构建联合推理框架。溯因推理（Abduction）的多元逻辑复杂关联性分析算法和数学方程式表达，同时还要考虑人类文化中的利益链、关系链、物理方程、化学方程、生物物种规律等的综合计算方法。
  在技术方法上，可以在知识图谱中应用溯因推理，结合生成模型和强化学习。部分论文中提到的RLF-KG方法，使用Transformer生成假设，并通过强化学习优化，这可以作为算法的基础框架。此外，法律逻辑学的文档中提到的多元溯因法和多级溯因法，在实际场景中需要考虑多种可能原因的联合作用，这可能涉及到概率模型或逻辑组合。

AAAI2025和ACL2024的论文中讨论在知识图谱中应用溯因推理，结合生成模型和强化学习。比如，论文中提到的RLF-KG方法，使用Transformer生成假设，并通过强化学习优化，这可以作为算法的基础框架。此外，法律逻辑学的文档中提到的多元溯因法和多级溯因法，说明需要考虑多种可能原因的联合作用，这可能涉及到概率模型或逻辑组合。

在人类文化中涉及到的利益链和关系链（对普通动物而言可能相关性较小，在设计与动物交互的人工智能模型中需要按需剔除），这可能涉及到经济学中的乘数效应和产业链模型。在商业领域资源产业链价格传导机制和利益分配趋向，可以用数学方程如乘数效应公式和博弈论中的纳什均衡来描述。

在物理方程方面，用户可能希望将守恒定律或动力学方程融入推理过程。例如，动量守恒或能量守恒方程可以作为约束条件，确保假设符合物理规律。化学方程则可能需要考虑反应动力学和平衡方程，比如质量作用定律，来验证假设的可行性。

生物物种规律方面，物种多样性指数（如Shannon-Wiener指数）和遗传学中的哈迪-温伯格定律，可以用于评估生物假设的合理性。例如，在医疗诊断中，结合基因频率和遗传规律来推导可能的病因。

数学表达方面，可能需要将不同领域的方程转化为统一的概率框架，如贝叶斯网络中的联合概率分布，或者使用张量分解来降维处理复杂的多模态数据。例如，结合知识图谱的多元组和物理方程，构建高阶张量进行联合推理。

核心算法框架与数学表达式
1） 逻辑假设生成与强化学习融合

• 基于知识图谱的生成模型（RLF-KG）：采用Transformer生成逻辑假设（H），通过近端策略优化（PPO）最小化观察（O）与假设结论的差异。数学表达为：
  

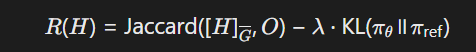
  其中，Jaccard指数衡量假设与观察的重合度，KL散度约束策略偏移。

• 多元假设联合推理：通过析取范式（DNF）整合多源假设，例如：
  

  表示假设由多个逻辑子句的“或”组合构成。

2） 动态利益链建模

• 产业链价格传导方程：引入乘数效应描述利益分配趋向：
  

  其中，(k_i)为产业链第i环节的产量比例系数，反映利益链中价格波动对上下游的影响。

• 博弈论与纳什均衡：构建多主体利益博弈模型，优化策略选择：
  

---

跨领域规律性约束的数学表达
1）物理与化学方程约束

• 守恒定律嵌入：
  例如动量守恒方程作为假设验证条件：
  
  用于机械系统故障溯因中的力学合理性检验。

• 化学反应动力学：结合质量作用定律评估假设可行性：
  

  通过速率常数(k)验证化学事故原因的动力学匹配度。

2）生物与生态规律

• 物种多样性指数：使用Shannon-Wiener指数量化生态假设的合理性：
  

  结合基因频率（如哈迪-温伯格定律）验证遗传病溯因假设。

• 种群动态模型：Logistic方程约束生物群落演化假设：
  

  用于流行病传播路径的溯因推理。

---

综合型计算方法
1） 多模态张量网络

• 高阶张量表示：将知识图谱实体、物理参数、化学属性等映射为张量：

• [
  \mathcal{T} = \sum_{i,j,k} \mathbf{v}_i \otimes \mathbf{r}_j \otimes \mathbf{p}_k
  ]
  其中(\mathbf{v}_i)为实体向量，(\mathbf{r}_j)为关系矩阵，(\mathbf{p}_k)为物理/化学属性向量。

• 联合概率推理：基于马尔可夫逻辑网络（MLN）整合多领域规则：
  

  权重(w_i)由神经网络动态学习。

2） 动态资源分配与优化

• 异构计算调度：针对神经-符号混合任务设计专用硬件加速（如CogSys框架）：
  
  优化GPU与符号处理单元（nsPE）的负载均衡。

• 增量式逻辑归纳（ILP）：从数据中自动生成领域规则：
  

  用于医疗诊断中未观测病理机制的假设补全。

---

验证与评估体系
1） 跨领域一致性验证

• Jaccard-Smatch联合指标：
  结合结构相似性（Smatch）与内容重合度（Jaccard）。
• 伦理约束层：注入规则过滤歧视性假设（如种族术语黑名单），确保输出符合社会规范。

2） 可解释性增强

• 逻辑规则可视化：生成假设推导链（如“实体→关系→约束”路径图），支持临床诊断报告的可信度评估。
• 时间感知嵌入：区分历史词源（如古拉丁语“virtus”）与现代语义，避免历时歧义。

---

溯因推理的复杂关联性分析需构建**“逻辑-数据-领域知识”三元驱动模型**，通过张量网络融合多模态规律、强化学习优化动态假设生成、博弈论建模利益链互动。未来方向包括：

• 量子-经典混合计算：利用量子退火加速大规模组合优化问题；
• 跨学科知识蒸馏：将物理/化学方程抽象为可微规则嵌入神经网络；
• 伦理约束的自动化注入：开发基于因果图的偏见检测算法。

该方法在医疗诊断、产业链风险预测、生态保护等领域具有广泛应用潜力，其数学严谨性与领域适应性将推动认知智能的范式升级。

---

3. 动态调度策略
   • 自适应工作负载调度（adSCH）：根据任务类型分配计算资源，例如：
     • 神经任务：优先调用GPU并行计算单元处理卷积/全连接层；
     • 符号任务：使用可重构处理单元（nsPE）执行循环卷积等操作。
   • 时空映射优化：通过数据流分割与并行化减少计算延迟，例如气泡流（BS）数据流设计。

---

4.7、挑战与优化方向

1. 知识获取瓶颈

   • 规则自动化生成：通过归纳逻辑编程（ILP）从少量标注数据中提取规则，但需解决规则复杂度限制（如单链式规则）。
   • 跨模态知识融合：整合文本、图像等多模态数据构建统一符号表示。

2. 计算效率提升

   • 硬件协同设计：如通过专用加速器（面积增加<5%）实现推理加速，支持实时溯因推理。
   • 近似推理算法：牺牲部分精度以降低计算复杂度，例如蒙特卡洛逻辑采样。
     **- 混杂逻辑设计：**结合不同的业务判断下，采用不同的逻辑链条，人工智能模型进行主动参与对人的博弈，如欺诈策略、协同策略来与人工智能交互方进行协同

3. 伦理与安全性

   • 规则约束注入：在符号层加入伦理过滤规则（如禁止歧视性推理），确保输出符合社会规范。
   • 对抗鲁棒性：通过符号逻辑验证神经网络输出的合理性，防止对抗样本误导推理。

---

4.8、一般应用场景

1. 医疗诊断：结合医学影像（神经网络）与临床指南（符号规则），生成可解释的诊断报告。
2. 机器人导航：神经模块处理传感器数据，符号模块执行路径规划（如A*算法与动态障碍物规避规则）。
3. 数学问题求解：分解复杂问题为子任务（神经模块计算数值解，符号模块验证逻辑一致性）。

---

神经符号系统的核心在于平衡“神经灵活性”与“符号严谨性”，其算法表达式需动态适应任务需求。未来突破可能依赖于异构计算架构与跨模态知识表示的深度协同，推动AI从感知智能向认知智能跃迁。

语料对模型决策的影响性分析

一、数据质量与多样性

1. 数据重复率

   • 负面影响：高重复数据导致模型记忆特定模式，降低泛化能力（0.1%数据重复100次可使模型性能下降至小模型水平）；数据之间无任何相关性，无前因推理、过程相关性、思维归纳、数学方程式表达等内容，导致是混杂性质的语料，难以拆解和找出核心价值。
   • 解决方案：通过去重算法（如MinHash）减少冗余。

2. 数据多样性

   • 跨领域语料：医疗、法律、金融等多领域数据提升模型在复杂场景的适应性。
   • 语言多样性：方言、网络用语增强语言理解广度（如网页7指出跨文化文本提升多语境迁移能力）。

二、数据结构与逻辑性

1. 结构化数据

   • 代码与数学逻辑：编程代码、数学题等强逻辑数据提升模型推理能力（此类数据构建认知结构）。
   • 标注信息：因果链、时间线等语义标注帮助模型提取深层逻辑。

2. 低质量语料风险

   • 噪声与偏见：社交平台未过滤语料可能包含歧视性内容，导致模型输出偏见（建议引入数据清洗与伦理审查——需要对思维逻辑比较强、对各类词语语句理解能力强的加入语句判断环境）。
   • 时效性：过期数据导致时间错配

---

综合影响模型决策的关键因素

因素	影响机制	优化方向	备注
数据重复	记忆过拟合，泛化能力下降	去重算法、动态采样
领域多样性	多场景适应性增强	跨领域混合训练
结构化逻辑	推理与任务规划能力提升	引入代码/数学题等规模式数据
标注质量	决定模型理解精度	人工审核、自动化标注工具

---