为什么t检验要满足正态？

因为t检验本质上是一种参数检验，是均值的比较。当我们进行t检验进行假设检验时都会使用以下假设：H0:两组之间的均值相等 ；H1:两组之间的均值不等 。t检验其实仅仅是对两组之间的均值进行了比较，但是为啥呢，正态分布不是有俩参数嘛——均值、标准差，为啥比一个均数就能说两样本代表的总体之间是否存在差异呢？我们发现t检验的前提条件除了要求数据来自正态分布总体外，还要求两样本总体方差相等,即具有方差齐性。举个栗子，看图说话：如果不要求满足正态分布，那么如下图，正态分布和指数分布比，比均数比个锤子，均数没有差异也没有任何意义，两总体之间肯定存在差异。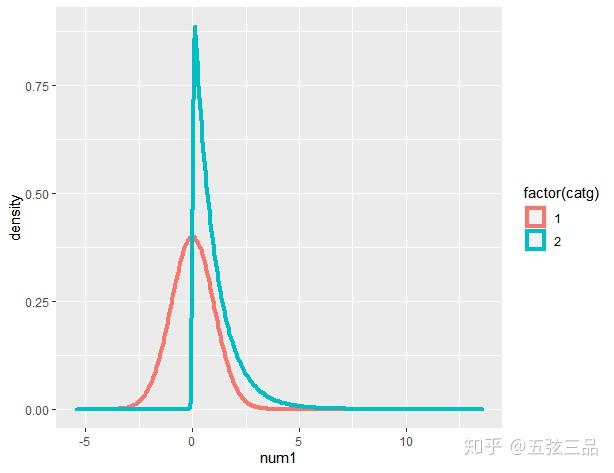再举个栗子，如果不要求方差齐，仅仅均值没差异也是没有意义的，你能说这两组没差异吗。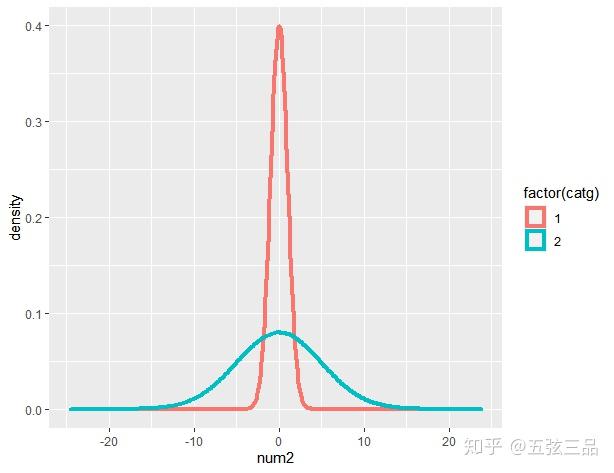我们可以发现，t检验的前提要求，限制了总体的其他参数，只剩下了均值来决定总体的分布，因此t检验时2个样本均值的比较才有意义。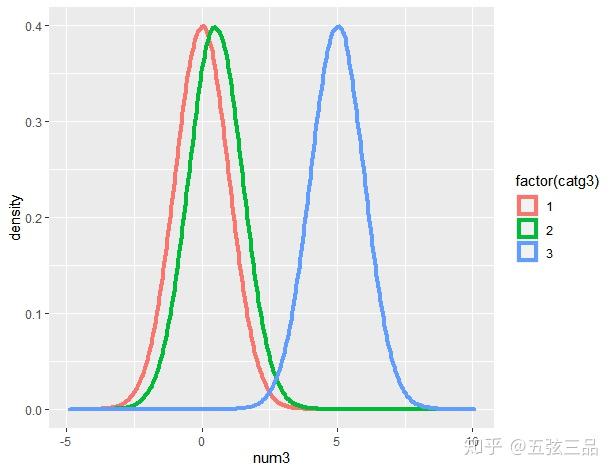t检验然而，这不是说我们所比较的总体必须要是正态分布，因为我们所比较的是平均值。不论从那种分布抽取的样本所得的平均值，只要样本数量越多(n>50)，平均值的分布都会越倾向为正态的，这就是所谓的中心极限定理。所以，我们要搞清楚的是，要满足正态分布的，不是总体的分布，而是平均值的分布。我们的六西格玛绿带课程中，有一些制作得很生动的动画，会解释得更清楚。

作者：五弦三品
链接：https://www.zhihu.com/question/397871872/answer/1250967307
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。