旋转公式和矩阵对数

在csdn上换点积分，感兴趣可以看知乎这个链接：

罗德里格旋转公式和矩阵对数 - Mr.Bo的文章 - 知乎 https://zhuanlan.zhihu.com/p/369659467

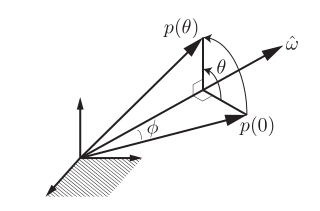
这样p（t）矢量末端的线速度 \dot p 可以表示为：

\\ \dot p=\hat\omega\times p=\left[\hat\omega\right]p

这个式子和我们之前介绍的向量微分方程如出一辙，因此它的解为：

\\p（t）=e^{\left[\hat\omega\right]t}p(0)

那意味着p（0）绕轴旋转后的新位置为：

\\p（\theta）=e^{\left[\hat\omega\right]\theta}p(0)

接着我们进一步展开这个式子，由于 \left[\hat\omega\right] 是斜对称阵，运算一下就有 \left[\hat\omega\right]^3=-\left[\hat\omega\right]\\ \left[\hat\omega\right]^4=-\left[\hat\omega\right]^2\\ \left[\hat\omega\right]^5=-\left[\hat\omega\right]^3

这样：

继续化简，可以看出括号内正好和sin和cos的麦克劳林级数有联系：

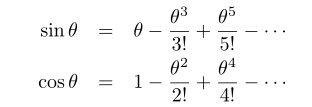
这样就有了下面这个描述：

对于一个向量 \hat\omega\theta\in R^3 ， \theta 是任意标量， \hat\omega 是单位向量, \left[\hat\omega\right]\theta=\left[\hat\omega\theta\right]\in SO(3) , 绕轴\hat\omega\in R^3,{||\hat\omega||=1} 旋转 \theta 的旋转矩阵就可以写成：

上式就是著名的Rodrigues’formula。

通过这种方式，我们就可以很方便的完成旋转操作。比如我们要对3x3的矩阵B进行旋转，那么 e^{\left[\hat\omega\right]\theta}B 表示在定系中绕 \hat\omega 轴旋转θ， Be^{\left[\hat\omega\right]\theta} 表示在动系中绕 \hat\omega 轴旋转θ。

纯理论是不是过于抽象，这里我们举个例子：

图中定系s绕 \hat\omega=（0,0.866,0.5） 旋转30°，那么旋转矩阵就可以表示为：

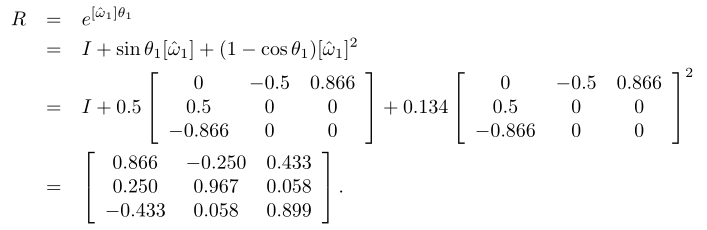
假设定系s的矩阵是单位阵I，那么转动后的新位置就是R，注意角度不同，旋转后的位置不一致。

接下来进一步进行讨论：

如果 \hat\omega\theta\in R^3 表示旋转矩阵R的指数坐标，那么斜对称阵 {\left[\hat\omega\right]\theta} 就是旋转矩阵R的矩阵对数（matrix logarithm）。通过这种方式，就在旋转矩阵和向量之间搭建了桥梁：

旋转矩阵表示为：

\\ R=\left[\begin{array}{ccc} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{array}\right]

为了推导矩阵对数，我们先将Rodrigues’formula展开：

式中， \hat{\omega}=\left(\hat{\omega}_{1}, \hat{\omega}_{2}, \hat{\omega}_{3}\right) ，cθ=cosθ，sθ=sinθ ,由于旋转矩阵是对称阵，对矩阵减去它的转置后我们可以得到：

上式中 sin（\theta）\not=0 ，就有：

上面解出的式子可以表示为斜对称阵：

由于 sin\theta 的存在，这里得做出讨论：

当 sin\theta\not=0 时，引入矩阵的迹：

因为 \hat{\omega}=\left(\hat{\omega}_{1}, \hat{\omega}_{2}, \hat{\omega}_{3}\right) 是单位向量，因此 \hat{\omega}_{1}^2+\hat{\omega}_{2}^2+\hat{\omega}_{3}^2=1 ，那么对于任意 \theta满足 trR=1+2cos\theta 且 sin\theta\not=0 ，旋转矩阵R就可以用指数坐标 e^{\left[\hat\omega\right]\theta} 来描述，其中：

当sin\theta=0 时， \theta=\pm k\pi,k\in Z ,

当k为偶数时，这意味着已经绕轴转回了 R=I ，所以转轴 \hat{\omega}=\left(\hat{\omega}_{1}, \hat{\omega}_{2}, \hat{\omega}_{3}\right) 没有被定义。

当k为奇数时，旋转矩阵可以表示为：

继续运算就有：

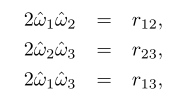
由于旋转矩阵是对称阵，因此所有元素都计算完毕了。

到这里，矩阵对数的推导就结束了，总结一下：

对于给出的旋转矩阵 R\in SO(3) ,绕单位旋转轴 \hat{\omega}\in R^3,{\|\hat{\omega}\|=1} 旋转一个角度 \theta \in[0,\pi] ,向量 \hat\omega\theta\in R^3 表示旋转矩阵R的指数坐标，斜对称阵 {\left[\hat\omega\right]\theta}\in so(3) 表示旋转矩阵R的矩阵对数（matrix logarithm ）。

就有以下情况：

（1）如果 R=I ,意味着 \theta =0 且旋转轴 \hat{\omega} 没有被定义

（2）如果 R=-1 ，意味着 \theta =\pi ,旋转轴 \hat{\omega} 的表示为下式三者任意一个：

（3）如果 \theta =arccos(\frac{1}{2}(trR-1))\in[0,\pi) ,那么：

满足上述三个条件中的一个，对于一个旋转矩阵R的指数坐标就存在一个矩阵对数。