回归分析过程

不易撞的网名

已于 2024-06-06 15:53:50 修改

阅读量1.2k

点赞数 25

分类专栏：机器学习文章标签：回归数据挖掘人工智能

于 2024-06-05 20:16:36 首次发布

本文链接：https://blog.csdn.net/weixin_50569789/article/details/139476240

版权

机器学习专栏收录该内容

221 篇文章 2 订阅

订阅专栏

什么是回归分析

相关分析是研究两个或两个以上的变量之间相关程度及大小的一种统计方法
回归分析是用来寻找存在相关关系的变量之间的一个数学表达式
也就是说，有些变量之间有着相关关系，但是他们的相关关系在之前一般用强弱或大小来评判，但是具体该怎么样进行一个衡量呢，有没有一个数学表达式能把这两个量连接在一起，这个就是回归分析

回归分析的基本思想是通过观察到的数据点来确定一**条“最佳拟合线”**或更复杂的曲线，这条线能够最接近地代表自变量和因变量之间的关系。这里的“最佳”通常是指误差（预测值与实际观测值之间的差异）的某种度量（如均方误差）最小化。

在对回归分析进行分类时，主要有两个分类方式：

根据变量的数目，可以分类一元回归、多元回归
根据自变量与因变量的表现形式，分为线性回归和非线性回归

所以，回归分析包括四个方向：一元线性回归分析、多元线性回归分析、一元非线性回归分析、多元非线性回归分析。

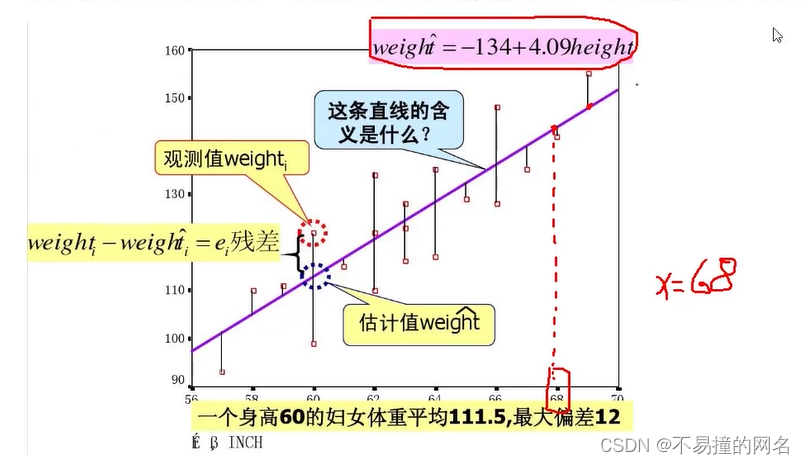
在这里插入图片描述

观测值（真实值）- 估计值（预测值） = 残差
基于历史数据中自变量与因变量的关系，基于回归方程预测出来更多的值，

回归分析的基本步骤

确定回归方程中的解释变量和被解释变量
确定回归模型，建立回归方程
对回归方程进行各种检验
利用回归方程进行预测

一元线性回归

$\beta_0 + \beta_1x+\varepsilon$

y叫做因变量或被解释变量
x叫做自变量或解释变量
$\beta_0表示截距$
$\beta_1表示斜率$
ε 表示误差项，反映除x和y之间的线性关系之外的随机因素对y的影响

假设一个冰淇淋店想要了解气温如何影响冰淇淋的销量。他们收集了一段时间内每天的气温（自变量，以摄氏度为单位）和当天的冰淇淋销量（因变量，以千支计）。通过回归分析，他们可以建立一个模型，比如：

$\beta_0 + \beta_1 \times 气温 + \varepsilon$

$\beta_0 是截距，表示在气温为0度时的预计销量$
$\beta_1 是气温的系数，表示气温每增加1度，销量预期增加的数量$
$\varepsilon 是误差项，代表不可预测的随机变化$

通过计算，如果得到 $\beta_1 = 2$
意味着气温每上升1摄氏度，冰淇淋销量平均增加2千支。这个模型可以帮助店主预测不同气温条件下的潜在销量，从而更好地规划库存和营销策略。

回归方程

描述因变量y的期望值如何依赖于自变量x的方程称为回归方程。根据对一元线性回归模型的假设，可以得到它的回归方程为:
$\beta_0 + \beta_1x$

如果回归方程中的参数已知，对于一个给定的x值，利用回归方程就能计算出y的期望值
用样本统计量代替回归方程中的未知参数，就得到估计的回归方程，简称回归直线

最小二乘法求参数

最小二乘法
根据已知的数据求得参数

利用回归直线进行估计和预测

点估计：利用估计的回归方程，对于x的某一个特定的值，求出y的一个估计值就是点估计
区间估计：利用估计的回归方程，对于x的一个特定值，求出y的一个估计值的区间就是区间估计

估计标准误差的计算

为了度量回归方程的可靠性，通常计算估计标准误差。它度量观察值回绕着回归直线的变化程度或分散程度。

估计标准误差

$S_y = \sqrt{\frac{\mathrm{\sum (y-\hat{y})^2}}{\mathrm{n-2}}}$

公式中根号内的分母是n-2,而不是n，因而自由度为n-2。
估计标准误差越大，则数据点围绕回归直线的分散程度就越大，回归方程的代表性越小。
估计标准误差越小，则数据点围绕回归直线的分散程度越小，回归方程的代表愈大，其可靠性越高。

置信区间估计:

$\hat{y}_0 \pm t_\frac{\mathrm{\alpha }}{\mathrm{2}}S_e\sqrt{\frac{1}{n}+\frac{\mathrm{(x_0-\bar{x})^2}}{\mathrm{\sum (x-\bar{x})^2}}}$

在1-α置信水平下预测区间为:
$\hat{y}_0 \pm t_\frac{\mathrm{\alpha }}{\mathrm{2}}S_e\sqrt{1+\frac{1}{n}+\frac{\mathrm{(x_0-\bar{x})^2}}{\mathrm{\sum (x-\bar{x})^2}}}$

$t_\frac{\mathrm{\alpha }}{\mathrm{2}}称为t分布的临界值，其值由t_\frac{\mathrm{\alpha }}{\mathrm{2}}(n-k)求得，其中n-k是自由度，具体值可查阅t分布表或者使用统计软件和计算器获得$

影响区间宽度的因素

置信水平(1-α)，区间宽度随置信水平的增大而增大
数据的离散程度Se，区间宽度随离程度的增大而增大
样本容量，区间宽度随样本容量的增大而减小
X0与X均值之间的差异，随着差异程度的增大而增大

衡量标准（回归直线的拟合优度）

回归直线与各观测点的接近程度称为回归直线对数据的拟合优度

总平方和（SST）
$\sum (y-\bar{y})^2$
回归平方和（SSR）
$\sum (\hat{y}-\bar{y})^2$
残差平方和（SSE）
$\sum (y-\hat{y})^2$

$y是实际值，\bar{y}是均值，\hat{y}是预测值（估计值）$
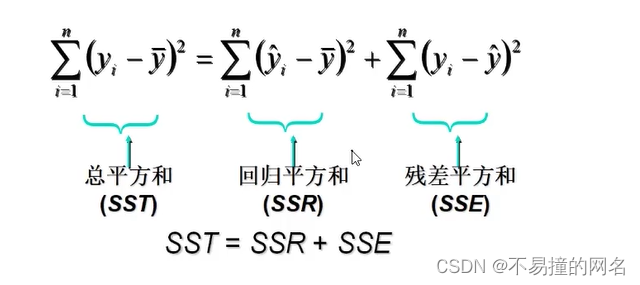
总平方和可以分解为回归平方和、残差平方和两部分：SST=SSR+SSE

总平方和(SST)，反映因变量的n个观察值与其均值的总离差
回归平方和SSR反映了y的总变差中，由于x与y之间的线性关系引起的y的变化部分
残差平方和SSE反映了除了x对y的线性影响之外的其他因素对y变差的作用，是不能由回归直线来解释的y的变差部分

判定系数

判定系数是衡量这个回归方程好坏的最主要的因素
回归平方和占总平方和的比例，用R^2表示,其值在0到1之间。

$R^2==0:说明y的变化与x无关，x完全无助于解释y的变差$
$R^2==1:说明残差平方和为0，拟合是完全的，y的变化只与x有关$

$R^2 = \frac{SSR}{SST} = \frac{\sum (\hat{y}-\bar{y})^2}{\sum (y-\bar{y})^2} = 1- \frac{\sum (y-\hat{y})^2}{\sum (y-\bar{y})^2}$
在这里插入图片描述

检验

显著性检验

显著性检验的主要目的是根据所建立的估计方程用自变量x来估计或预测因变量y的取值。
当建立了估计方程后，还不能马上进行估计或预测，因为该估计方程是
根据样本数据得到的，它是否真实的反映了变量x和y之间的关系，则需要通过检验后才能证实。

根据样本数据拟合回归方程时，实际上就已经假定变量x与y之间存在着线性关系，并假定误差项是一个服从正态分布的随机变量，且具有相同的方差。但这些假设是否成立需要检验

显著性检验包括两方面:

线性关系检验
回归系数检验

线性关系检验

线性关系检验是检验自变量x和因变量y之间的线性关系是否显著，或者说，它们之问能否用一个线性模型来表示。

将均方回归 (MSR)同均方残差(MSE)加以比较，应用F检验来分析二者之间的差别是否显著。

均方回归：回归平方和SSR除以相应的自由度(自变量的个数K)
均方残差：残差平方和SSE除以相应的自由度(n-k-1)

$H0:\beta_1=0所有回归系数与零无显著差异，y与全体x的线性关系不显著$
计算检验统计量F:
$\frac{SSR/1}{SSE/n-2} = \frac{MSR}{MSE} \backsim F(1,n-2)$

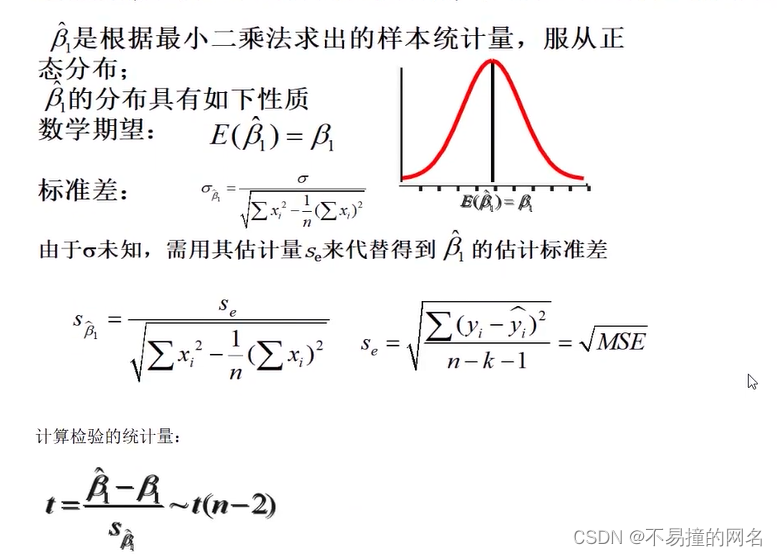
回归系数检验

回归系数显著性检验的目的是通过检验回归系数β的值与0是否有显著性差异，来判断Y与X之间是否有显著的线性关系
若β=0,则总体回归方程中不含X项(即Y不随X变动而变动)，因此，变量Y与X之间并不存在线性关系;
若β≠0,说明变量Y与X之间存在显著的线性关系。

在这里插入图片描述

线性关系检验与回归系数检验的区别

线性关系的检验是检验自变量与因变量是否可以用线性来表达
回归系数的检验是对样本数据计算的回归系数检验总体中回归系数是否为0

在一元线性回归中，自变量只有一个，线性关系检验与回归系数检验是等价的。
多元回归分析中，这两种检验的意义是不同的。
线性关系检验只能用来检验总体回归关系的显著性，而回归系数检验可以对各个回归系数分别进行检验

多元线性回归分析

经常会遇到某一现象的发展和变化取决于几个影响因素的情况，也就是一个因变量和几个自变量有依存关系的情况，这时需用多元线性回归分析。

多元线性回归分析预测法，是指通过对两上或两个以上的自变量与一个因变量的相关分析，建立预测模型进行预测和控制的方法。
多元线性回归预测模型一般式为:
$B_1x_1 + B_2x_2 + ... + B_nx_n + \varepsilon$

调整的多重判定系数:
用样本容量n和自变量的个数k去修正R^2得到
$R_a^2 = 1-(1-R^2) * \frac{n-1}{n-k-1}$

避免增加自变量而高估R^2

曲线回归分析

直线关系是两变量间最简单的一种关系，曲线回归分析的基本任务是通过两个相关变量x与y的实际观测数据建立曲线回归方程，以揭示x与y间的曲线联系的形式。

曲线回归分析最困难和首要的工作是确定自变量与因变量间的曲线关系的类型，曲线回归分析的基本过程:

先将x或y进行变量转换
对新变量进行直线回归分析、建立直线回归方程并进行显著性检验和区间估计
将新变量还原为原变量，由新变量的直线回归方程和置信区间得出原变量的曲线回归方程和置信区间

由于曲线回归模型种类繁多，所以没有通用的回归方程可直接使用。但是对于某些特殊的回归模型，可以通过变量代换、取对数等方法将其线性化，然后使用标准方程求解参数，再将参数带回原方程就是所求。

多重共线性

一元线性回归例子

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

nsample = 20
x = np.linspace(0, 10, nsample)
x

array([ 0.        ,  0.52631579,  1.05263158,  1.57894737,  2.10526316,
        2.63157895,  3.15789474,  3.68421053,  4.21052632,  4.73684211,
        5.26315789,  5.78947368,  6.31578947,  6.84210526,  7.36842105,
        7.89473684,  8.42105263,  8.94736842,  9.47368421, 10.        ])

在最小二乘法中，为了与常数项组合因此需要进行转换

X = sm.add_constant(x)
X
array([[  1.        ,   0.        ],
       [  1.        ,   0.52631579],
       [  1.        ,   1.05263158],
       [  1.        ,   1.57894737],
       [  1.        ,   2.10526316],
       [  1.        ,   2.63157895],
       [  1.        ,   3.15789474],
       [  1.        ,   3.68421053],
       [  1.        ,   4.21052632],
       [  1.        ,   4.73684211],
       [  1.        ,   5.26315789],
       [  1.        ,   5.78947368],
       [  1.        ,   6.31578947],
       [  1.        ,   6.84210526],
       [  1.        ,   7.36842105],
       [  1.        ,   7.89473684],
       [  1.        ,   8.42105263],
       [  1.        ,   8.94736842],
       [  1.        ,   9.47368421],
       [  1.        ,  10.        ]])

指定 β0,β1

#β0,β1分别设置成2,5
beta = np.array([2, 5])
beta
array([2, 5])

误差项（服从高斯分布）

e = np.random.normal(size=nsample)
e
array([-1.87955777, -0.49196542, -0.53259826, -0.10675137,  1.17508727,
       -1.02293335,  1.75717793, -1.12456907, -0.64294355,  0.44920794,
       -1.20471093,  0.02588779, -0.69216987,  1.23018605,  0.59180637,
        1.03269883,  0.16712902,  2.06599762, -2.06133608, -0.12899139])

实际值y

y = np.dot(X, beta) + e
y
array([  0.12044223,   4.13961353,   6.73055964,   9.78798547,
        13.70140306,  14.13496139,  19.54665161,  19.29648356,
        22.40968802,  26.13341847,  27.11107855,  30.97325622,
        32.8867775 ,  37.44071236,  39.43391164,  42.50638304,
        44.27239218,  48.80283972,  47.30708497,  51.87100861])

最小二乘法

model = sm.OLS(y,X)

拟合数据

res = model.fit()

回归系数

res.params
array([ 1.49524076,  5.08701837])

全部结果

res.summary()

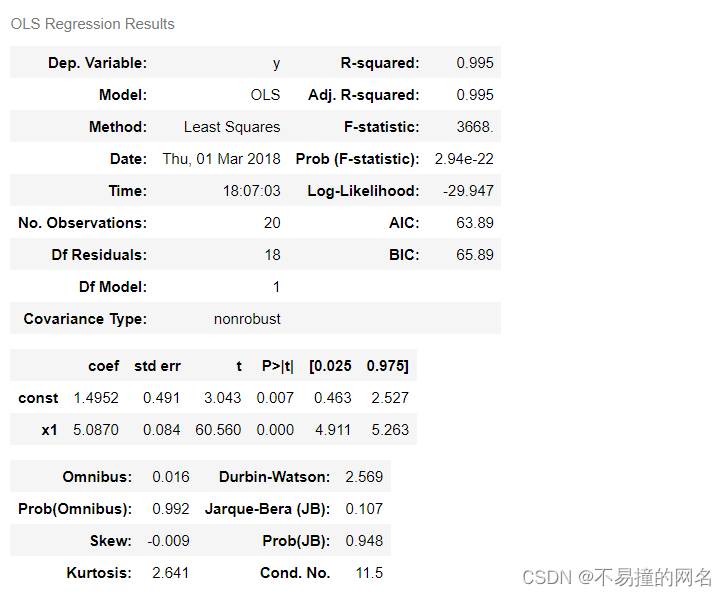
在这里插入图片描述
R-squared：就是R^2值
Adj.R-squared：就是调制后i的R^2值
Prob (F-statistic)：检验的概率值，越低则x和y的线性关系越强
const：代表bete0，常数项，第一列是其实际的指标值
x1：代表bete1

拟合的估计值

y_ = res.fittedvalues
y_
array([  1.49524076,   4.17261885,   6.84999693,   9.52737502,
        12.20475311,  14.8821312 ,  17.55950928,  20.23688737,
        22.91426546,  25.59164354,  28.26902163,  30.94639972,
        33.62377781,  36.30115589,  38.97853398,  41.65591207,
        44.33329015,  47.01066824,  49.68804633,  52.36542442])

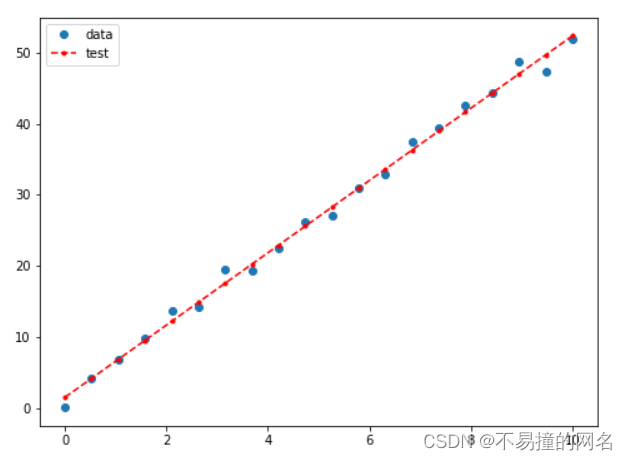
原始数据与拟合数据的可视化

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label='data')#原始数据
ax.plot(x, y_, 'r--.',label='test')#拟合数据
ax.legend(loc='best')
plt.show()

在这里插入图片描述

高阶线性回归例子

#Y=5+2⋅X+3⋅X^2
 
nsample = 50
x = np.linspace(0, 10, nsample)
X = np.column_stack((x, x**2))
X = sm.add_constant(X)

beta = np.array([5, 2, 3])
e = np.random.normal(size=nsample)
y = np.dot(X, beta) + e
model = sm.OLS(y,X)
results = model.fit()
results.params
array([ 4.93210623,  2.16604081,  2.97682135])

results.summary()

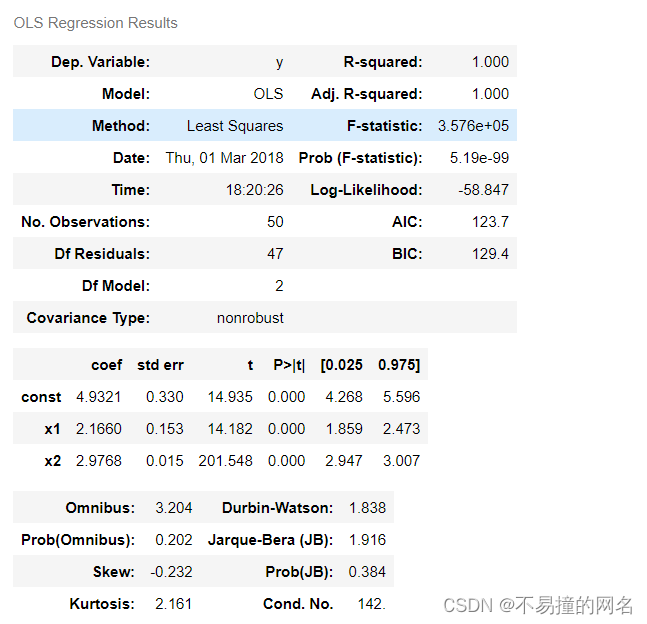
在这里插入图片描述

y_fitted = results.fittedvalues
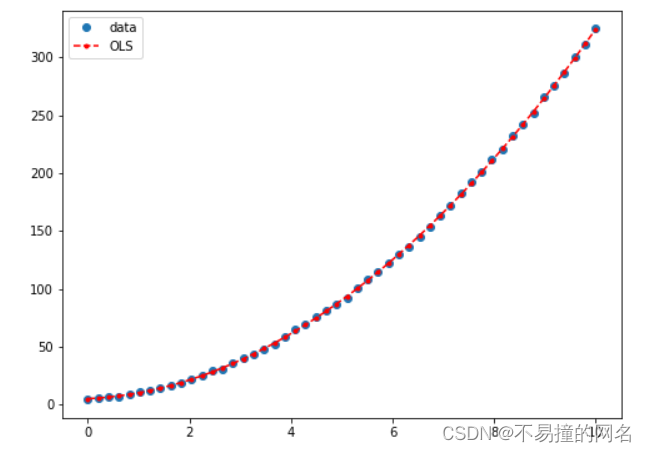
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label='data')
ax.plot(x, y_fitted, 'r--.',label='OLS')
ax.legend(loc='best')
plt.show()

在这里插入图片描述

分类变量例子

$假设分类变量有3个取值（a,b,c）,比如考试成绩有3个等级。那么a就是（1,0,0），b（0,1,0），c(0,0,1),这个时候就需要3个系数β_0,β_1,β_2，也就是β_0x_0+β_1x_1+β_2x_2$

nsample = 50
groups = np.zeros(nsample,int)
groups
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0])

groups[20:40] = 1
groups[40:] = 2
dummy = sm.categorical(groups, drop=True)
dummy

array([[ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.],
       [ 0.,  0.,  1.]])

#Y=5+2X+3Z1+6⋅Z2+9⋅Z3.
 
x = np.linspace(0, 20, nsample)
X = np.column_stack((x, dummy))
X = sm.add_constant(X)
beta = [5, 2, 3, 6, 9]
e = np.random.normal(size=nsample)
y = np.dot(X, beta) + e
result = sm.OLS(y,X).fit()
result.summary()

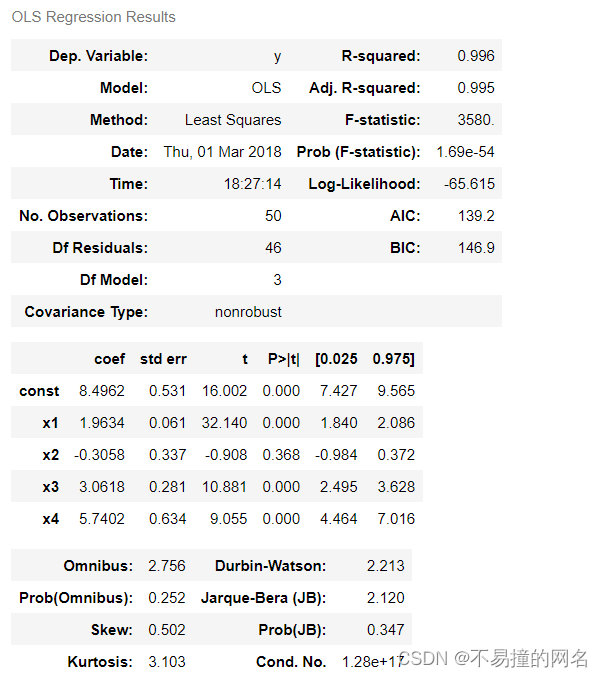
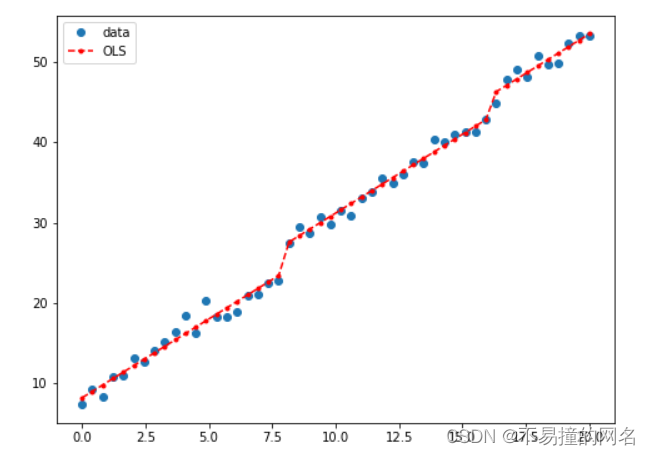
在这里插入图片描述

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, result.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best')
plt.show()

在这里插入图片描述
注意：主要分析过程可能会包括缺失值填充，就是将Null舍去或者取其列均值进行填充。也可能包括数据预处理，就是将内容转换为计算机可识别的数据

不易撞的网名

关注

25
点赞
踩
21

收藏

觉得还不错? 一键收藏
打赏
0
评论
回归分析过程

相关分析是研究两个或两个以上的变量之间相关程度及大小的一种统计方法回归分析是用来寻找存在相关关系的变量之间的一个数学表达式也就是说，有些变量之间有着相关关系，但是他们的相关关系在之前一般用强弱或大小来评判，但是具体该怎么样进行一个衡量呢，有没有一个数学表达式能把这两个量连接在一起，这个就是回归分析回归分析的基本思想是通过观察到的数据点来确定一**条“最佳拟合线”**或更复杂的曲线，这条线能够最接近地代表自变量和因变量之间的关系。
复制链接

扫一扫