Frequency and Spatial Dual Guidance for Image Dehazing

🥰诚心希望此篇文章能帮助到您，感谢您的观看🥰。

摘要

现有方法的不足：现有的基于深度学习的方法主要是利用空间信息而忽略了可区分的频率信息。

作者提出了：通过共同利用空间域和频率域的信息来进行去雾。为了实现频率域和空间域的双重引导，精心开发了两个核心设计：频域中的幅度引导相位模块和空间域中的全局引导局部模块。前者通过深度傅里叶变换处理全局频率信息，并在幅度谱的指导下重建相位谱，而后者则整合了上述全局频率信息，以方便空间域的局部特征学习。

什么是频率域和空间域？
参考自：从信号的角度理解图像内容
图像可以看作是一种信号，如下图一张图像，黑线把可以把图像分成x轴和y轴，x轴和y轴的范围都是[0,300]，在x轴和y轴不同位置处，其对应的像素值就可以画出右图和左下图，这个就是图像的空间域。而根据傅里叶变换，其可以转化为对应的频率域，这两条曲线可以由多个不同的频率的正弦函数或余弦函数组成，其中，频率高的就对应图像的中边缘和细节，而频率低的就是一些平滑的部分，对图像进行增强，可以把低频的信息给去除掉，只保留高频信息，而平滑正好相反，保留低频的信息。

引言

雾霾是一种常见的大气现象，由悬浮在靠近地面的空气中的微小水滴或冰晶组成，在雾天环境下捕获的图像的对比度和视觉外观等视觉质量明显下降，图像去雾的目标是从有雾图像中恢复清晰图像，一些高级计算机视觉任务如目标检测、场景理解受到朦胧场景中捕获的输入图像的很大影响。因此，在过去的十年中，从模糊的照片中恢复清晰的照片一直是计算摄影和视觉社区的研究重点。

从输入的单张有雾图像中估计出清晰图像是一个没有唯一解的问题，并且非常具有挑战性。传统方法依赖于物理散射模型和使用各种图像先验来制定相应的解空间。然而，这些手工设计的先验通常都是基于特定的观察，这对于去模拟图像的内在特征和估计物理散射模型中的传输图并不可靠。

尽管目前这些基于深度学习的方法在图像去雾上都取得了显著的进步，但是它们都没有利用到图像的空间信息并且忽略了可区分的频率信息，而相比于在空间域上进行处理，频域中模糊图像对和清晰图像对之间的差异在物理上是比较明显且易于区分。因此，找到雾霾恶化与频率之间的相关性对于理解去雾问题非常重要。

在本文中，我们揭示了雾霾恶化与频域中的幅度谱和相位谱特征之间的关系，如下图：

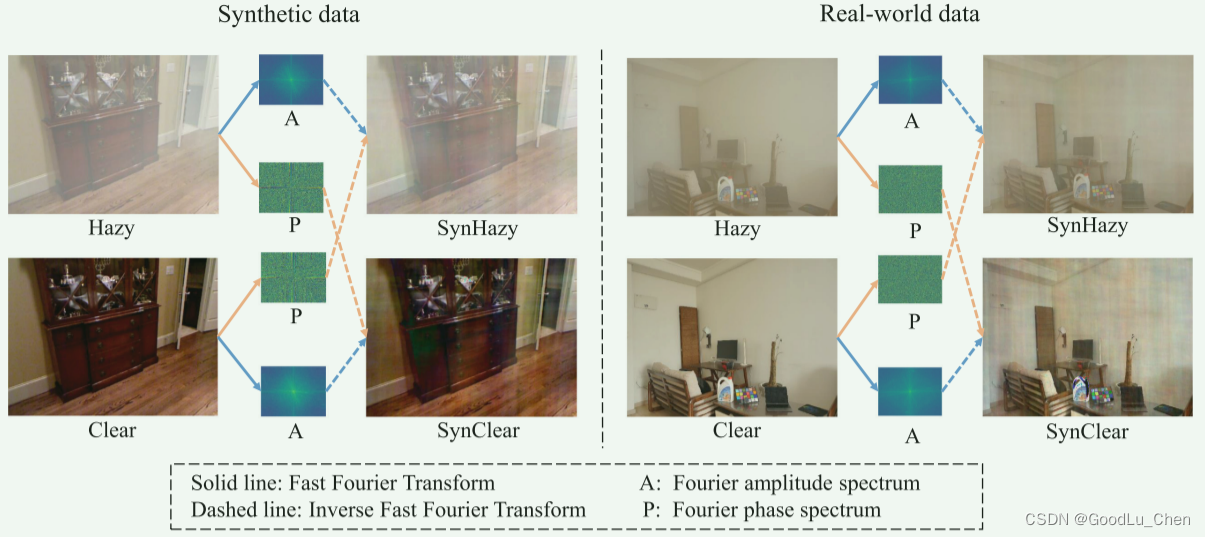
具体来说，我们首先通过快速傅里叶变换将空间域图像变换为频域幅度和相位谱，然后交换雾图和清晰图像对的幅度和相位谱，最后，通过快速傅里叶逆变换将交换后的光谱变换回Synclear和SynHazy图像，从上述图中我们可以观察到：
（1）Clear 和 SynClear有相同的幅度谱但相位谱不同，它们看起来很相似
（2）Clear和SynHazy有相同的相位谱但是不同的幅度谱，它们看起来不同
所以可以得到下面的结论：
（1）雾霾引起的退化特性主要表现在幅度谱上
（2）有雾图像对和清晰图像对的相位谱之间的差异很小

为了进一步的解释和验证该结论，作者使用50对雾图和清晰图来得到其对应的SynClear和SynHazy，然后使用t-SNE来绘制得到下面的图形。

可以很明显的看到Clear和SynClear是聚集在一起的，这是非常高的相似性分布，同时hazy和SynHazy也是非常接近的。

基于上述观察和结论，作者提出了频率和空间双引导的图像去雾网络，通过联合的利用频率域和空间域的信息。为了去实现频率和空间的双引导，本文精心设计了两个组件，一个是在频率域上的幅度引导相位模块，另一个是在空间域上的全局引导局部模块，具体来说，AGP模块通过深度傅里叶变换处理全局频率信息，并在幅度谱的指导下重建相位谱，而GGL模块集成了上述全局频率信息，便于在空域中进行局部特征学习。

总的来说，本文的贡献主要有：

1. 揭示了雾退化和幅度谱和相位谱之间的统计特性之间的相关性，并且集成了频率信息和空间信息来进行图像去雾
2. 提出了一个频率和空间双引导的网络来进行有效的生成高质量的无雾图像，这是第一篇把频率域和空间域引入到图像去雾任务中的网络
3. 精心设计了GGL和AGP模块来进行空间和频率域的引导

相关工作

单幅图像去雾

基于物理先验

但是这种方法通常是针对特定场景，这使得各个空间位置的雾霾形成具有空间变化和非均匀性，因此，仅仅通过物理先验来估计传输图来进行去雾通常不能很好的描述雾霾退化。

基于深度学习

基于深度学习的方法利用神经网络来学习先验或者是直接学习雾图到清晰图的转化。尽管现有的深度学习方法在图像去雾上展示了非常优越的性能，然而，这些深度学习方法都没有利用到频率域中的信息，这不能很好的建模雾退化的特性，本文的方法在傅立叶域中工作，揭示了幅度-相位与雾度退化之间的关系。

傅里叶变换的应用

DeepRFT [34]将卷积运算应用于频域频谱的实部和虚部以恢复模糊图像，FDIT [7]将图像分解为低频和高频分量以增强图像生成过程。然而，现有的基于频率的方法忽略了建立频率特性和图像退化之间的关系。与现有技术不同，我们进一步发现雾霾退化与频域中幅度和相位谱特征之间的相关性，并定制设计AGP模块以利用这一观察结果。

方法

前言

我们方法的启发是来自于观察雾霾退化和通过傅里叶变换得到的频率域中的频谱图和相位谱图特性的关系得到的。并且通过上述结论，我们知道雾霾引起的退化主要是表现在图像的幅度谱上，清晰图和其对应的无雾图的相位谱很接近。图像的照明对比度由幅度谱表示，而纹理结构信息则用相位谱来表示。因此，本文的结论是和这个理论符合的（红色的），因为雾主要是图像的照明对比度，雾会使图像的对比度下降，照明变的灰蒙蒙。而结构信息是不受雾霾退化的影响的。

此外，因为清晰图和合成清晰图的相位谱差异很小，因此，可以通过幅度谱的学习残差来引导相位谱的复原，作者根据这些观察，设计出了AGP。

作者的第二个观察如下：😶😶‍🌫️😐

空间域中进行图像去雾的全局和局部建模之间的差异，通过基于 CNN 的网络的有限感受野来解释它们的差异，感受野可以定义为在输出像素中，输入像素对该像素有影响的区域。卷积操作有着有限的感受野，现有的基于CNN的方法不能考虑到中某一像素的除了感受野以外的其他像素内容（long-range dependency：在cv领域，就是考虑一个像素的时候同时考虑其邻域，甚至是邻域的邻域）和理解雾霾分布的上下文。

对于图像去雾任务来说，当浓雾区域比感受野更大的时候，落入到感受野中的部分浓雾块无法获取足够的信息来进行去雾，如果要重建一副清晰的图像，应该需要去获取图像的全局信息，基于上述观察，作者设计出了全局引导的局部模块，使得其模型可以建模全局信息。

网络结构

本文采用了一种双分支的网络结构，因为每一个分支都可以集中在他自己的信息处理过程，不同的分支可以提出不同的表示，所以，如果我们充分的利用不同的信息并且引入适当的引导，两个分支中的综合性的信息就可以显著提高图像去雾的性能。

网络结构如下图：😳

网络结构包含两个分支，一个是频率分支，也就是上分支，称为全局分支。另一个是空间分支，也就是下分支，称为局部分支。

输入一张图像$I$，上分支输出$J^{\prime }$，下分支输出最终的去雾图$J_{out}$，$J$表示相应的有雾图对应的真值图像。对于频率分支，通过精心设计的幅度引导相位（AGP）模块，AGP在频率域运行，处理的信息是全局信息。此外，为了充分利用恢复的全局信息并为局部特征学习引入全局指导，我们引入了全局引导局部（GGL）模块，为U-Net架构的每个阶段的局部特征学习提供全局信息。

AGP

相位比振幅传达更多有关图像结构的信息，并且高度不受噪声和对比度失真的影响，因此，雾引起的退化主要是表现在幅度谱上，而对相位的影响更小一些，换句话说，雾主要是影响图像的对比度和亮度，由于整个图像的可视性降低，对图像的结构影响较小。基于上述想法，作者提出了APG。
AGP的过程：

1. AGP模块首先将空间域特征$x$变换为其频域傅立叶变换$\mathcal{F}(x)$，公式如下：
   $\mathcal{F}(x)(u,v)={\sum }_{h=0}^{H-1}{\sum }_{w=0}^{W-1}x(h,w)e^{-j2\pi \left(\frac{h}{H}u+\frac{w}{W}v\right)}.$
   频域特征$\mathcal{F}(x)$表示为$\mathcal{F}(x)=\mathcal{R}(x)+j\mathcal{I}(x)$
   其中$\mathcal{R}(x)$表示其实部，$\mathcal{I}(x)$表示其虚部，然后把实部和虚部转化为幅度谱和相位谱：
   $$\mathcal{A}(x)(u,v)={\left[{\mathcal{R}}^2(x)(u,v)+{\mathcal{I}}^2(x)(u,v)\right]}^{1/2}$$
   $$\mathcal{P}(x)(u,v)=\arctan \left[\frac{\mathcal{I}(x)(u,v)}{\mathcal{R}(x)(u,v)}\right]$$

其中，$\mathcal{A}(x)$是幅度谱，$\mathcal{P}(x)$是相位谱，鉴于幅度谱严重失真，而相位谱失真较小，首先使用1×1的卷积来复原幅度谱，然后，通过复原后的幅度谱减去输入的幅度谱得到幅度谱残差${\mathcal{A}}_{res}(x)$，公式如下：

$$\begin{array}{rl}& {\mathcal{A}}^{{}^{\prime }}(x)(u,v)=\mathcal{A}(x)(u,v)\otimes k_1,\\ & {\mathcal{A}}_{res}(x)(u,v)={\mathcal{A}}^{{}^{\prime }}(x)(u,v)-\mathcal{A}(x)(u,v),\end{array}$$

其中，$\otimes$表示卷积操作，在本篇论文中，$k_s$表示卷积核大小为$s\times s$的卷积操作。

接着，把获得的幅度谱残差进行全局平均池化得到(batch,channel,1,1)大小特征图，再使用softmax对channel上的值进行归一化，使其总和为1，得到注意力图注意力图$\mathcal{A}tten(x)$。过程如下：

$$\mathcal{A}tten(x)(u,v)=Softmax\left[GAP\left({\mathcal{A}}_{res}(x)(u,v)\right)\right]$$

$${\mathcal{P}}^{{}^{\prime }}(x)(u,v)=[\mathcal{A}tten(x)(u,v)\odot \mathcal{P}(x)(u,v)]\otimes k_1+\mathcal{P}(x)(u,v)$$

再对幅度谱和相位谱进行复原以后，我们把其重新转换为复数的实部和虚部：
$$\begin{gathered} {\mathcal{R}}^{{}^{\prime }}(x)(u,v)={\mathcal{A}}^{{}^{\prime }}(x)(u,v)\cos {\mathcal{P}}^{{}^{\prime }}(x)(u,v), \\ {\mathcal{I}}^{{}^{\prime }}(x)(u,v)={\mathcal{A}}^{{}^{\prime }}(x)(u,v)\sin {\mathcal{P}}^{{}^{\prime }}(x)(u,v). \end{gathered}$$
最后，通过逆傅里叶变换把频率域特征${\mathcal{F}}^{{}^{\prime }}(x)={\mathcal{R}}^{{}^{\prime }}(x)+j{\mathcal{I}}^{{}^{\prime }}(x)$转化回空间域特征$AGP(x)$。

下图展示了在不同设置条件下生产出来的特征，特征(d)是通过将全局信息引导引入局部特征(b)而产生的，可以很明显的的观察到，在使用GGL模块后，特征(d)不仅结构良好，而且细节精美且伪影较少，这意味着特征（d）结合了局部特征（b）和全局特征（c）的优点，正如我们理想的预期。

GGL

由于局部分支在比较在前面的网络层具有有限的感受野，网络不能够去捕获其领域的领域的像素的信息，因此没有足够的能力去移除一些局部区域的雾，因此，本文提出了GGL模块，在GGL模块，将全局分支的编码器和解码器中同一阶段的特征合并起来，以指导本地分支的相应编码器阶段中的局部特征，具体来说，首先连接来自全局分支的两个全局特征，然后执行简单的卷积去获得$G^n$：

$$G^n=Cat\left(G_{encoder}^n,G_{decoder}^n\right)\otimes k_3$$

然后使用上述得到的全局特征去引导第n步的局部特征$L^n$。 首先通过下面的操作得到$Ou{t}_{scale}^n$，

$$Ou{t}_{scale}^n=(G^n\otimes k_1\otimes k_1)\odot L^n$$

然后，使用获得的$Ou{t}_{scale}^n$，引入$G^n$的移位操作去获得n步GGL模块的输出：

$$Ou{t}^n=(G^n\otimes k_1\otimes k_1)+Ou{t}_{scale}^n.$$

频率和空间双引导网络损失函数

训练过程中的损失包括空间域和频率域的损失函数，由以下几项组成：

$${\mathcal{L}}_{cha}=\sqrt{{\left(J_{out}\left(x\right)-J\left(x\right)\right)}^2+\epsilon }+\sqrt{{\left(J^{\prime }\left(x\right)-J\left(x\right)\right)}^2+\epsilon },$$

$${\mathcal{L}}_{amp}=\frac{2}{UV}\sum _{u=0}^{U/2-1}\sum _{v=0}^{V-1}\left({\Vert |A_{out}{|}_{u,v}-|A{|}_{u,v}\Vert }_1+{\Vert |A^{\prime }{|}_{u,v}-|A{|}_{u,v}\Vert }_1\right),$$
$${\mathcal{L}}_{pha}=\frac{2}{UV}\sum _{u=0}^{U/2-1}\sum _{v=0}^{V-1}\left({\Vert |P_{out}{|}_{u,v}-|P{|}_{u,v}\Vert }_1+{\Vert |P^{\prime }{|}_{u,v}-|P{|}_{u,v}\Vert }_1\right)$$

其中$\epsilon =1\times e^{-12}$，并且$u$的求和仅执行到$U/2-1$，因为所有频率分量的 50% 是冗余的。 因此，我们网络的总损失 L 表示为：

$$\mathcal{L}={\mathcal{L}}_{cha}+\beta \left({\mathcal{L}}_{amp}+{\mathcal{L}}_{pha}\right),$$
其中，$\beta$设置为了0.1。

实验

在合成和真实世界数据集上进行了实验，对于合成数据集，采用的是RESIDE数据集，RESIDE室内训练集（ITS）包含13990张雾图，这些雾图是从1399张清晰图中产生出来的，合成目标测试集（SOTS）包含500张室内雾图和500张室外雾图，本文使用ITS作为训练集，SOTS作为测试集。此外，为了去评估该FSDGN的鲁棒性，本文也采用了两个真实世界数据集：Dense-Haze和NH-HAZE。
Dense-Haze包含浓雾和均匀雾场景图片，NH-HAZE包含非均匀雾场景图片，两个数据集都包含55对配对数据集。

下图是定量比较结果：⬇️⬇️⬇️⬇️

可以发现，作者的方法在几乎所有的指标上都比SOTA方法好（除了Param和GFLOPs）。

下图是在RESIDE数据集上的定性比较结果图：▶️▶️▶️▶️

▶️▶️▶️▶️
⬇️⬇️⬇️⬇️⬇️下图是在NH-HAZE和Dense-HAZE数据集上的定性比较结果图：