Orthogonal Matrices
8.1 正交单位向量
- 如果一个向量集合
a
1
,
a
2
,
.
.
.
,
a
n
∈
R
m
a_1,a_2,...,a_n\in R^m
a1,a2,...,an∈Rm满足:
- 向量有单位范数: ∣ ∣ a i ∣ ∣ = 1 ||a_i||=1 ∣∣ai∣∣=1
- 向量之间相互正交:如果
i
≠
j
i≠j
i=j,有
a
i
T
a
j
=
0
a_i^Ta_j=0
aiTaj=0
则称这些向量是标准正交的。
- 例子:

8.2 标准正交矩阵
- 如果A的Gram矩阵为单位矩阵,则
A
∈
R
m
×
n
A\in R^{m×n}
A∈Rm×n具有标准正交列:

8.3 矩阵-向量乘积
- 如果
A
∈
R
m
×
n
A\in R^{m×n}
A∈Rm×n具有标准正交列,则线性函数
f
(
x
)
=
A
x
f(x)=Ax
f(x)=Ax
- 保持原内积
- 保持原范数
- 保持原距离
- 保持原角度
8.4 左可逆性
- 如果矩阵
A
∈
R
m
×
n
A\in R^{m×n}
A∈Rm×n有标准正交列,则:
- A是左可逆的,其左逆 A T A^T AT,根据定义: A T A = I A^T A=I ATA=I
- A有线性无关的列向量
- A是高的或者方的<维度定理>
8.5 正交矩阵
- 定义:所有列凉凉相互正交的方形实矩阵称为正交矩阵
- 正交矩阵满足非奇异性,即如果矩阵A是正交的,则:

<注意:如果 A ∈ R m × n A\in R^{m×n} A∈Rm×n有标准正交列以及 m > n m>n m>n,则 A A T ≠ I AA^T≠I AAT=I>
8.6 置换矩阵
- 让Font metrics not found for font: .为 ( 1 , 2 , … , 𝑛 ) (1,2,…,𝑛) (1,2,…,n)的一个重新排序的排列。
- 将𝜋与一个置换矩阵
A
∈
R
𝑛
×
𝑛
A∈ℝ^{𝑛×𝑛}
A∈Rn×n联系起来:
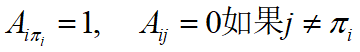
- 𝐴𝑥是𝑥的一个置换:Font metrics not found for font: .。
- A在每一行和每一列中都有一个等于1的元素。
- 置换矩阵满足正交性,即所有置换矩阵都是正交的:
-
𝐴
𝑇
𝐴
=
𝐼
𝐴^𝑇 𝐴=𝐼
ATA=I,因为A的每一行有一个元素等于1:
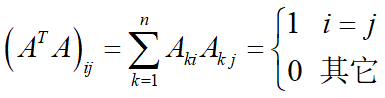
- A T = A − 1 A^T=A^{-1} AT=A−1是逆置换矩阵
-
𝐴
𝑇
𝐴
=
𝐼
𝐴^𝑇 𝐴=𝐼
ATA=I,因为A的每一行有一个元素等于1:
【例子】

8.7 平面旋转
- 在一个平面的旋转可以用矩阵表示为:


- 在
R
n
R^n
Rn的坐标平面上旋转,例如:
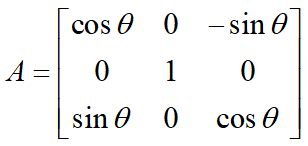
描述了在 R 3 R^3 R3中 ( x 1 , x 3 ) (x_1,x_3) (x1,x3)平面的旋转。
8.8 反射算子
- 反射算子(reflector):一个矩阵的形式为:
A = I − 2 a a T A=I-2aa^T A=I−2aaT
其中,向量a满足 ∣ ∣ a ∣ ∣ 2 = 1 ||a||_2=1 ∣∣a∣∣2=1 - 性质:
- 反射矩阵(reflector matrix)是对称的 A T = A A^T=A AT=A
- 反射矩阵(reflector matrix)是正交的

8.8.1 反射算子的几何解释


8.8.2 练习

8.9 正交矩阵的乘积
- 若
A
1
,
.
.
.
,
A
k
∈
R
n
×
n
A_1,...,A_k\in R^{n×n}
A1,...,Ak∈Rn×n是正交矩阵,那么它们的乘积为:
A = A 1 A 2 . . . A k A=A_1A_2...A_k A=A1A2...Ak
正交性:

8.10 具有正交矩阵的线性方程
- 系数正交矩阵
A
∈
R
n
×
n
A\in R^{n×n}
A∈Rn×n的线性方程:
A x = b Ax=b Ax=b
的解为:
x = A − 1 b = A T b x=A^{-1}b=A^Tb x=A−1b=ATb - 可以在 2 n 2 2n^2 2n2个flop内计算矩阵向量乘法。
- 如果A有特殊性子和,代价将会小于
n
2
n^2
n2。例如:
- 置换矩阵:0 flop
- 反射算子(给定a):4n flops
- 平面旋转:O(1) flop
8.11 标准列正交的高矩阵
- 假设矩阵
A
∈
R
m
×
n
A\in R^{m×n}
A∈Rm×n是高的(m>n),具有标准正交列,则有:
A T A^T AT具有标准正交行 -
A
T
A^T
AT是A的一个左逆
A T A = I A^TA=I ATA=I - A没有右逆,因为:
A A T ≠ I AA^T≠I AAT=I
8.12 值域范围
- 一个向量集合张成的空间是其所有线性组合的集合:

- 矩阵
A
∈
R
m
×
n
A\in R^{m×n}
A∈Rm×n的范围为其列向量张成的空间:
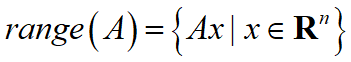
- 例子:
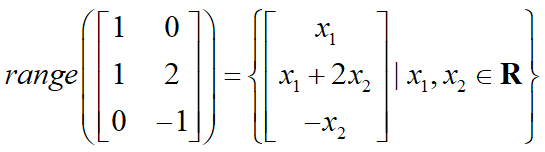
8.13 值域投影

8.13.1 验证

8.14 Gram矩阵
- 如果
𝐴
∈
C
(
𝑚
×
𝑛
)
𝐴∈ℂ^(𝑚×𝑛)
A∈C(m×n)的Gram矩阵为单位矩阵,则𝐴具有正交列:

- 列有单位范数: ‖ 𝑎 𝑖 ‖ 2 2 = 𝑎 𝑖 𝐻 𝑎 𝑖 = 1 ‖𝑎_𝑖 ‖_2^2=𝑎_𝑖^𝐻 𝑎_𝑖=1 ‖ai‖22=aiHai=1
- 列是相互正交的:对于 𝑖 ≠ 𝑗 𝑖≠𝑗 i=j, 𝑎 𝑖 𝐻 𝑎 𝑗 = 0 𝑎_𝑖^𝐻 𝑎_𝑗=0 aiHaj=0
8.15 Unitary矩阵
- 定义:列正交的方形复数矩阵称为酉矩阵
- 酉矩阵的逆:

- 酉矩阵是具有逆 A H A^H AH的非奇异矩阵
- 如果A是酉矩阵,那么 A H A^H AH也是酉矩阵








 本文介绍了正交单位向量、标准正交矩阵及其性质,包括保持内积、范数、距离和角度不变。讨论了左可逆性、置换矩阵、平面旋转和反射算子,特别强调了正交矩阵在解决线性方程组中的应用以及值域和投影的概念。还涉及了Gram矩阵和酉矩阵等主题。
本文介绍了正交单位向量、标准正交矩阵及其性质,包括保持内积、范数、距离和角度不变。讨论了左可逆性、置换矩阵、平面旋转和反射算子,特别强调了正交矩阵在解决线性方程组中的应用以及值域和投影的概念。还涉及了Gram矩阵和酉矩阵等主题。
















 1600
1600

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








